Physics:Cavendish experiment

Short description: Experiment measuring the force of gravity (1797–1798)

Cavendish's diagram of his torsion pendulum, seen from above. The pendulum consists of two small spherical lead weights (h, h) hanging from a 6-foot horizontal wooden beam supported in the center by a fine torsion wire. The beam is protected from air currents inside a wooden box (A, A, A, A). The two large weights (W, W) attached to a separate suspension attract the small weights, causing the beam to rotate slightly. The rotation is read off of vernier scales (S) at either end of the rod. The large weights can be rotated to the other side of the torsion beam (w, w), causing the beam to rotate in the opposite direction.

The Cavendish experiment, performed in 1797–1798 by English scientist Henry Cavendish, was the first experiment to measure the force of gravity between masses in the laboratory and the first to yield accurate values for the gravitational constant. Because of the unit conventions then in use, the gravitational constant does not appear explicitly in Cavendish's work. Instead, the result was originally expressed as the specific gravity of Earth, or equivalently the mass of Earth. His experiment gave the first accurate values for these geophysical constants.

The experiment was devised sometime before 1783 by geologist John Michell, who constructed a torsion balance apparatus for it. However, Michell died in 1793 without completing the work. After his death the apparatus passed to Francis John Hyde Wollaston and then to Cavendish, who rebuilt the apparatus but kept close to Michell's original plan. Cavendish then carried out a series of measurements with the equipment and reported his results in the Philosophical Transactions of the Royal Society in 1798.

The experiment

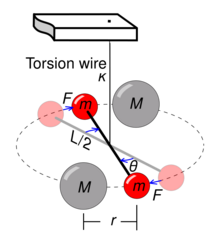
The apparatus consisted of a torsion balance made of a six-foot (1.8 m) wooden rod horizontally suspended from a wire, with two 2-inch-diameter (51 mm), 1.61-pound (0.73 kg) lead spheres, one attached to each end. Two massive 12-inch (300 mm), 348-pound (158 kg) lead balls, suspended separately, could be positioned away from or to either side of the smaller balls, 8.85 inches (225 mm) away. The experiment measured the faint gravitational attraction between the small and large balls, which deflected the torsion balance rod by about 0.16" (or only 0.03" with a stiffer suspending wire).

Vertical section drawing of Cavendish's torsion balance instrument including the building in which it was housed. The large balls were hung from a frame so they could be rotated by a pulley from outside. Figure 1 of Cavendish's paper

Detail showing torsion balance arm (m), large ball (W), small ball (x), and isolating box (ABCDE).

The two large balls could be positioned either away from or to either side of the torsion balance rod. Their mutual attraction to the small balls caused the arm to rotate, twisting the suspension wire. The arm rotated until it reached an angle where the twisting force of the wire balanced the combined gravitational force of attraction between the large and small lead spheres. By measuring the angle of the rod and knowing the twisting force (torque) of the wire for a given angle, Cavendish was able to determine the force between the pairs of masses. Since the gravitational force of the Earth on the small ball could be measured directly by weighing it, the ratio of the two forces allowed the relative density of the Earth to be calculated, using Newton's law of gravitation.

Cavendish found that the Earth's density was 5.448±0.033 times that of water (due to a simple arithmetic error, found in 1821 by Francis Baily, the erroneous value 5.480±0.038 appears in his paper). The current accepted value is 5.514 g/cm³.

To find the wire's torsion coefficient, the torque exerted by the wire for a given angle of twist, Cavendish timed the natural oscillation period of the balance rod as it rotated slowly clockwise and counterclockwise against the twisting of the wire. For the first 3 experiments the period was about 15 minutes and for the next 14 experiments the period was half of that, about 7.5 minutes. The period changed because after the third experiment Cavendish put in a stiffer wire. The torsion coefficient could be calculated from this and the mass and dimensions of the balance. Actually, the rod was never at rest; Cavendish had to measure the deflection angle of the rod while it was oscillating.

Cavendish's equipment was remarkably sensitive for its time. The force involved in twisting the torsion balance was very small, 1.74×10⁻⁷ N, (the weight of only 0.0177 milligrams) or about ​¹⁄_50,000,000 of the weight of the small balls. To prevent air currents and temperature changes from interfering with the measurements, Cavendish placed the entire apparatus in a mahogany box about 1.98 meters wide, 1.27 meters tall, and 14 cm thick,[1] all in a closed shed on his estate. Through two holes in the walls of the shed, Cavendish used telescopes to observe the movement of the torsion balance's horizontal rod. The key observable was of course the deflection of the torsion balance rod, which Cavendish measured to be about 0.16" (or only 0.03" for the stiffer wire used mostly). Cavendish was able to measure this small deflection to an accuracy of better than 0.01 inches (0.25 mm) using vernier scales on the ends of the rod. The accuracy of Cavendish's result was not exceeded until C. V. Boys' experiment in 1895. In time, Michell's torsion balance became the dominant technique for measuring the gravitational constant (G) and most contemporary measurements still use variations of it.

Cavendish's result provided additional evidence for a planetary core made of metal, an idea first proposed by Charles Hutton based on his analysis of the 1774 Schiehallion experiment. Cavendish's result of 5.4 g·cm⁻³, 23% bigger than Hutton's, is close to 80% of the density of liquid iron, and 80% higher than the density of the Earth's outer crust, suggesting the existence of a dense iron core.

Reformulation of Cavendish's result to G

The formulation of Newtonian gravity in terms of a gravitational constant did not become standard until long after Cavendish's time. Indeed, one of the first references to G is in 1873, 75 years after Cavendish's work.

Cavendish expressed his result in terms of the density of the Earth. He referred to his experiment in correspondence as 'weighing the world'. Later authors reformulated his results in modern terms.

[math]\displaystyle{ G = g\frac{R_\text{earth}^2}{M_\text{earth}} = \frac{3g}{4\pi R_\text{earth}\rho_\text{earth}}\, }[/math]

After converting to SI units, Cavendish's value for the Earth's density, 5.448 g cm⁻³, gives

G = 6.74×10⁻¹¹ m³ kg^–1 s⁻²,

which differs by only 1% from the 2014 CODATA value of 6.67408×10⁻¹¹ m³ kg⁻¹ s⁻². Today, physicists often use units where the gravitational constant takes a different form. The Gaussian gravitational constant used in space dynamics is a defined constant and the Cavendish experiment can be considered as a measurement of this constant. In Cavendish's time, physicists used the same units for mass and weight, in effect taking g as a standard acceleration. Then, since R_earth was known, ρ_earth played the role of an inverse gravitational constant. The density of the Earth was hence a much sought-after quantity at the time, and there had been earlier attempts to measure it, such as the Schiehallion experiment in 1774.

Derivation of G and the Earth's mass

For the definitions of terms, see the drawing below and the table at the end of this section.

The following is not the method Cavendish used, but describes how modern physicists would calculate the results from his experiment. From Hooke's law, the torque on the torsion wire is proportional to the deflection angle [math]\displaystyle{ \theta }[/math] of the balance. The torque is [math]\displaystyle{ \kappa\theta }[/math] where [math]\displaystyle{ \kappa }[/math] is the torsion coefficient of the wire. However, a torque in the opposite direction is also generated by the gravitational pull of the masses. It can be written as a product of the attractive force of a large ball on a small ball and the distance L/2 to the suspension wire. Since there are two pairs of balls, each experiencing force F at a distance L/2 from the axis of the balance, the torque due to gravitational force is LF. At equilibrium (when the balance has been stabilized at an angle [math]\displaystyle{ \theta }[/math]), the total amount of torque must be zero as these two sources of torque balance out. Thus, we can equate their magnitudes given by the formulas above, which gives the following:

[math]\displaystyle{ \kappa\theta\ = LF \, }[/math]

For F, Newton's law of universal gravitation is used to express the attractive force between a large and small ball:

Simplified diagram of torsion balance

[math]\displaystyle{ F = \frac{G m M}{r^2}\, }[/math]

Substituting F into the first equation above gives

[math]\displaystyle{ \kappa\theta\ = L\frac{GmM}{r^2} \qquad\qquad\qquad(1)\, }[/math]

To find the torsion coefficient ([math]\displaystyle{ \kappa }[/math]) of the wire, Cavendish measured the natural resonant oscillation period T of the torsion balance:

[math]\displaystyle{ T = 2\pi\sqrt{\frac{I}{\kappa}} }[/math]

Assuming the mass of the torsion beam itself is negligible, the moment of inertia of the balance is just due to the small balls. Treating them as point masses, each at L/2 from the axis, gives:

[math]\displaystyle{ I = m\left (\frac{L}{2}\right )^2 + m\left (\frac{L}{2}\right )^2 = 2m\left (\frac{L}{2}\right )^2 = \frac{mL^2}{2}\, }[/math],

and so:

[math]\displaystyle{ T = 2\pi\sqrt{\frac{mL^2}{2\kappa}}\, }[/math]

Solving this for [math]\displaystyle{ \kappa }[/math], substituting into (1), and rearranging for G, the result is:

[math]\displaystyle{ G = \frac{2 \pi^2 L r^2 \theta}{M T^2} \, }[/math].

Once G has been found, the attraction of an object at the Earth's surface to the Earth itself can be used to calculate the Earth's mass and density:

[math]\displaystyle{ mg = \frac{GmM_{\rm earth}}{R_{\rm earth}^2}\, }[/math]

[math]\displaystyle{ M_{\rm earth} = \frac{gR_{\rm earth}^2}{G}\, }[/math]

[math]\displaystyle{ \rho_{\rm earth} = \frac{M_{\rm earth}}{\tfrac{4}{3} \pi R_{\rm earth}^3} = \frac{3g}{4 \pi R_{\rm earth} G}\, }[/math]

Definitions of terms

Symbol	Unit	Definition
[math]\displaystyle{ \theta }[/math]	radians	Deflection of torsion balance beam from its rest position
F	N	Gravitational force between masses M and m
G	m3 kg−1 s−2	Gravitational constant
m	kg	Mass of small lead ball
M	kg	Mass of large lead ball
r	m	Distance between centers of large and small balls when balance is deflected
L	m	Length of torsion balance beam between centers of small balls
[math]\displaystyle{ \kappa }[/math]	N m rad−1	Torsion coefficient of suspending wire
I	kg m2	Moment of inertia of torsion balance beam
T	s	Period of oscillation of torsion balance
g	m s−2	Acceleration of gravity at the surface of the Earth
Mearth	kg	Mass of the Earth
Rearth	m	Radius of the Earth
[math]\displaystyle{ \rho }[/math]earth	kg m−3	Density of the Earth

References

Sources

• Boys, C. Vernon (1894). "On the Newtonian constant of gravitation". Nature 50 (1292): 330–334. doi:10.1038/050330a0. Bibcode: 1894Natur..50..330.. https://books.google.com/books?id=ZrloHemOmUEC&pg=PA353. Retrieved 2013-12-30. 
• Cavendish, Henry (1798). "Experiments to Determine the Density of the Earth". Philosophical Transactions of the Royal Society 88: 469–526. doi:10.1098/rstl.1798.0022. 
• Clotfelter, B. E. (1987). "The Cavendish experiment as Cavendish knew it". American Journal of Physics 55 (3): 210–213. doi:10.1119/1.15214. Bibcode: 1987AmJPh..55..210C.  Establishes that Cavendish didn't determine G.
• Falconer, Isobel (1999). "Henry Cavendish: the man and the measurement". Measurement Science and Technology 10 (6): 470–477. doi:10.1088/0957-0233/10/6/310. Bibcode: 1999MeScT..10..470F. 
• Hodges, Laurent (1999). "The Michell-Cavendish Experiment, faculty website, Iowa State Univ.". http://www.public.iastate.edu/~lhodges/Michell.htm. Retrieved 2013-12-30.  Discusses Michell's contributions, and whether Cavendish determined G.
• Jungnickel; McCormmach (1996). Cavendish. Philadelphia, Pennsylvania: American Philosophical Society. ISBN 978-0-87169-220-7. https://archive.org/details/bub_gb_EUoLAAAAIAAJ. Retrieved 2013-12-30. 
• Lally, Sean P. (1999). "Henry Cavendish and the Density of the Earth". The Physics Teacher 37 (1): 34–37. doi:10.1119/1.880145. Bibcode: 1999PhTea..37...34L. 
• Poynting, John H. (1894). The Mean Density of the Earth: An essay to which the Adams prize was adjudged in 1893. London: C. Griffin & Co.. https://archive.org/details/meandensityeart00poyngoog. Retrieved 2013-12-30.  Review of gravity measurements since 1740.

External links

• Cavendish’s experiment in the Feynman Lectures on Physics
• Sideways Gravity in the Basement, The Citizen Scientist, July 1, 2005. Homebrew Cavendish experiment, showing calculation of results and precautions necessary to eliminate wind and electrostatic errors.
• "Big 'G'", Physics Central, retrieved Dec. 8, 2013. Experiment at Univ. of Washington to measure the gravitational constant using variation of Cavendish method.
• Eöt-Wash Group, Univ. of Washington. "The Controversy over Newton's Gravitational Constant". http://www.npl.washington.edu/eotwash/bigG. Retrieved December 8, 2013. . Discusses current state of measurements of G.
• Model of Cavendish's torsion balance, retrieved Aug. 28, 2007, at Science Museum, London.