Physics:Stern–Gerlach experiment
| Part of a series on |
| Quantum mechanics |
|---|
| [math]\displaystyle{ i \hbar \frac{\partial}{\partial t} | \psi (t) \rangle = \hat{H} | \psi (t) \rangle }[/math] |
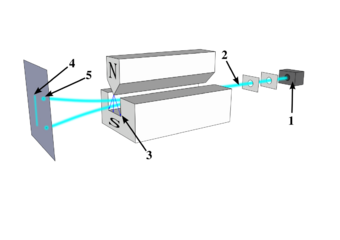
In quantum physics, the Stern–Gerlach experiment demonstrated that the spatial orientation of angular momentum is quantized. Thus an atomic-scale system was shown to have intrinsically quantum properties. In the original experiment, silver atoms were sent through a spatially-varying magnetic field, which deflected them before they struck a detector screen, such as a glass slide. Particles with non-zero magnetic moment were deflected, owing to the magnetic field gradient, from a straight path. The screen revealed discrete points of accumulation, rather than a continuous distribution,[1] owing to their quantized spin. Historically, this experiment was decisive in convincing physicists of the reality of angular-momentum quantization in all atomic-scale systems.[2][3][4]
After its conception by Otto Stern in 1921, the experiment was first successfully conducted with Walther Gerlach in early 1922.[1][5][6]
Description
File:Quantum spin and the Stern-Gerlach experiment.ogv
The Stern–Gerlach experiment involves sending silver atoms through an inhomogeneous magnetic field and observing their deflection.
The results show that particles possess an intrinsic angular momentum that is closely analogous to the angular momentum of a classically spinning object, but that takes only certain quantized values. Another important result is that only one component of a particle's spin can be measured at one time, meaning that the measurement of the spin along the z-axis destroys information about a particle's spin along the x and y axis.
The experiment is normally conducted using electrically neutral particles such as silver atoms. This avoids the large deflection in the path of a charged particle moving through a magnetic field and allows spin-dependent effects to dominate.[7][8]
If the particle is treated as a classical spinning magnetic dipole, it will precess in a magnetic field because of the torque that the magnetic field exerts on the dipole (see torque-induced precession). If it moves through a homogeneous magnetic field, the forces exerted on opposite ends of the dipole cancel each other out and the trajectory of the particle is unaffected. However, if the magnetic field is inhomogeneous then the force on one end of the dipole will be slightly greater than the opposing force on the other end, so that there is a net force which deflects the particle's trajectory. If the particles were classical spinning objects, one would expect the distribution of their spin angular momentum vectors to be random and continuous. Each particle would be deflected by an amount proportional to the dot product of its magnetic moment with the external field gradient, producing some density distribution on the detector screen. Instead, the particles passing through the Stern–Gerlach apparatus are deflected either up or down by a specific amount. This was a measurement of the quantum observable now known as spin angular momentum, which demonstrated possible outcomes of a measurement where the observable has a discrete set of values or point spectrum.
Although some discrete quantum phenomena, such as atomic spectra, were observed much earlier, the Stern–Gerlach experiment allowed scientists to directly observe separation between discrete quantum states for the first time in the history of science.
Theoretically, quantum angular momentum of any kind has a discrete spectrum, which is sometimes briefly expressed as "angular momentum is quantized".
Experiment using particles with +1⁄2 or −1⁄2 spin
If the experiment is conducted using charged particles like electrons, there will be a Lorentz force that tends to bend the trajectory in a circle. This force can be cancelled by an electric field of appropriate magnitude oriented transverse to the charged particle's path.
Electrons are spin-1⁄2 particles. These have only two possible spin angular momentum values measured along any axis, [math]\displaystyle{ +\frac{\hbar}{2} }[/math] or [math]\displaystyle{ -\frac{\hbar}{2} }[/math], a purely quantum mechanical phenomenon. Because its value is always the same, it is regarded as an intrinsic property of electrons, and is sometimes known as "intrinsic angular momentum" (to distinguish it from orbital angular momentum, which can vary and depends on the presence of other particles). If one measures the spin along a vertical axis, electrons are described as "spin up" or "spin down", based on the magnetic moment pointing up or down, respectively.
To mathematically describe the experiment with spin [math]\displaystyle{ +\frac{1}{2} }[/math] particles, it is easiest to use Dirac's bra–ket notation. As the particles pass through the Stern–Gerlach device, they are deflected either up or down, and observed by the detector which resolves to either spin up or spin down. These are described by the angular momentum quantum number [math]\displaystyle{ j }[/math], which can take on one of the two possible allowed values, either [math]\displaystyle{ +\frac{\hbar}{2} }[/math] or [math]\displaystyle{ -\frac{\hbar}{2} }[/math]. The act of observing (measuring) the momentum along the [math]\displaystyle{ z }[/math] axis corresponds to the operator [math]\displaystyle{ J_z }[/math].[specify] In mathematical terms, the initial state of the particles is
- [math]\displaystyle{ |\psi\rangle = c_1\left|\psi_{j = +\frac{\hbar}{2}}\right\rangle + c_2\left|\psi_{j = -\frac{\hbar}{2}}\right\rangle }[/math]
where constants [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] are complex numbers. This initial state spin can point in any direction. The squares of the absolute values [math]\displaystyle{ |c_1|^2 }[/math] and [math]\displaystyle{ |c_2|^2 }[/math] determine the probabilities that for a system in the initial state [math]\displaystyle{ |\psi\rangle }[/math] one of the two possible values of [math]\displaystyle{ j }[/math] is found after the measurement is made. The constants [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math] must also be normalized in order that the probability of finding either one of the values be unity, that is we must ensure that [math]\displaystyle{ |c_1|^2 + |c_2|^2 = 1 }[/math]. However, this information is not sufficient to determine the values of [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math], because they are complex numbers. Therefore, the measurement yields only the squared magnitudes of the constants, which are interpreted as probabilities.
Sequential experiments
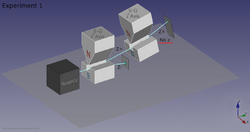
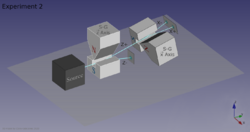
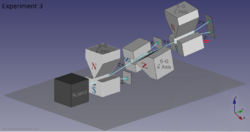
If we link multiple Stern–Gerlach apparatuses (the rectangles containing S-G), we can clearly see that they do not act as simple selectors, i.e. filtering out particles with one of the states (pre-existing to the measurement) and blocking the others. Instead they alter the state by observing it (as in light polarization). In the figure below, x and z name the directions of the (inhomogenous) magnetic field, with the x-z-plane being orthogonal to the particle beam. In the three S-G systems shown below, the cross-hatched squares denote the blocking of a given output, i.e. each of the S-G systems with a blocker allows only particles with one of two states to enter the next S-G apparatus in the sequence.[9]
Experiment 1
The top illustration shows that when a second, identical, S-G apparatus is placed at the exit of the first apparatus, only z+ is seen in the output of the second apparatus. This result is expected since all neutrons at this point are expected to have z+ spin, as only the z+ beam from the first apparatus entered the second apparatus.[10]
Experiment 2
The middle system shows what happens when a different S-G apparatus is placed at the exit of the z+ beam resulting of the first apparatus, the second apparatus measuring the deflection of the beams on the x axis instead of the z axis. The second apparatus produces x+ and x- outputs. Now classically we would expect to have one beam with the x characteristic oriented + and the z characteristic oriented +, and another with the x characteristic oriented - and the z characteristic oriented +.[10]
Experiment 3
The bottom system contradicts that expectation. The output of the third apparatus which measures the deflection on the z axis again shows an output of z- as well as z+. Given that the input to the second S-G apparatus consisted only of z+, it can be inferred that a S-G apparatus must be altering the states of the particles that pass through it. This experiment can be interpreted to exhibit the uncertainty principle: since the angular momentum cannot be measured on two perpendicular directions at the same time, the measurement of the angular momentum on the x direction destroys the previous determination of the angular momentum in the z direction. That's why the third apparatus measures renewed z+ and z- beams like the x measurement really made a clean slate of the z+ output.[10]
History
The Stern–Gerlach experiment was conceived by Otto Stern in 1921 and performed by him and Walther Gerlach in Frankfurt in 1922.[9] At the time, Stern was an assistant to Max Born at the University of Frankfurt's Institute for Theoretical Physics,[3] and Gerlach was an assistant at the same university's Institute for Experimental Physics.[3]
At the time of the experiment, the most prevalent model for describing the atom was the Bohr-Sommerfeld model,[11][12] which described electrons as going around the positively charged nucleus only in certain discrete atomic orbitals or energy levels. Since the electron was quantized to be only in certain positions in space, the separation into distinct orbits was referred to as space quantization. The Stern–Gerlach experiment was meant to test the Bohr–Sommerfeld hypothesis that the direction of the angular momentum of a silver atom is quantized.[13]
Note that the experiment was performed several years before George Uhlenbeck and Samuel Goudsmit formulated their hypothesis about the existence of electron spin in 1925.[14] Even though the result of the Stern−Gerlach experiment has later turned out to be in agreement with the predictions of quantum mechanics for a spin-1⁄2 particle, the experimental result was also consistent with the Bohr–Sommerfeld theory.[15]
In 1927, T.E. Phipps and J.B. Taylor reproduced the effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms.[16] However, in 1926 the non-relativistic Schrödinger equation had incorrectly predicted the magnetic moment of hydrogen to be zero in its ground state. To correct this problem Wolfgang Pauli introduced "by hand", so to speak, the 3 Pauli matrices which now bear his name, but which were later shown by Paul Dirac in 1928 to be intrinsic in his relativistic equation.[17][self-published source?]
The experiment was first performed with an electromagnet that allowed the non-uniform magnetic field to be turned on gradually from a null value.[1] When the field was null, the silver atoms were deposited as a single band on the detecting glass slide. When the field was made stronger, the middle of the band began to widen and eventually to split into two, so that the glass-slide image looked like a lip-print, with an opening in the middle, and closure at either end.[18] In the middle, where the magnetic field was strong enough to split the beam into two, statistically half of the silver atoms had been deflected by the non-uniformity of the field.
Importance
The Stern–Gerlach experiment strongly influenced later developments in modern physics:
- In the decade that followed, scientists showed using similar techniques, that the nuclei of some atoms also have quantized angular momentum.[example needed] It is the interaction of this nuclear angular momentum with the spin of the electron that is responsible for the hyperfine structure of the spectroscopic lines.[19]
- In the 1930s, using an extended version of the Stern–Gerlach apparatus, Isidor Rabi and colleagues showed that by using a varying magnetic field, one can force the magnetic moment to go from one state to the other.[citation needed] The series of experiments culminated in 1937 when they discovered that state transitions could be induced using time varying fields or RF fields. The so-called Rabi oscillation is the working mechanism for the Magnetic Resonance Imaging equipment found in hospitals.[citation needed]
- Norman F. Ramsey later modified the Rabi apparatus to increase the interaction time with the field. The extreme sensitivity due to the frequency of the radiation makes this very useful for keeping accurate time, and it is still used today in atomic clocks. [citation needed]
- In the early sixties, Ramsey and Daniel Kleppner used a Stern–Gerlach system to produce a beam of polarized hydrogen as the source of energy for the hydrogen maser, which is still one of the most popular frequency standards.
- The direct observation of the spin is the most direct evidence of quantization in quantum mechanics. [why?] [citation needed]
- The Stern–Gerlach experiment has become a prototype[20][21][22] for quantum measurement, demonstrating the observation of a single, real value (eigenvalue) of an initially unknown physical property. Entering the Stern-Gerlach magnet, the direction of the silver atom’s magnetic moment is indefinite, but it is observed to be either parallel, or anti-parallel to the direction of the magnetic field, B, at the exit of the magnet. Atoms with a magnetic moment parallel to B have been accelerated in that direction by the magnetic field gradient; those with anti-parallel moments were accelerated the opposite way. So, each atom traversing the magnet will strike the detector ((5) in the diagram) at just one of the two spots. According to quantum measurement theory, the wave function representing the atom’s magnetic moment is in a superposition of those two directions entering the magnet. A single, spin-direction eigenvalue is recorded when a momentum quantum is transferred, from the magnetic field, to the atom, initiating acceleration, and displacement, in that momentum direction.[23]
See also
- Photon polarization
- Stern–Gerlach Medal
- German inventors and discoverers
References
- ↑ 1.0 1.1 1.2 Gerlach, W.; Stern, O. (1922). "Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 9 (1): 349–352. doi:10.1007/BF01326983. Bibcode: 1922ZPhy....9..349G.
- ↑ Allan Franklin; Slobodan Perovic. "Experiment in Physics, Appendix 5". in Edward N. Zalta. The Stanford Encyclopedia of Philosophy (Winter 2016 ed.). https://plato.stanford.edu/archives/win2016/entries/physics-experiment/app5.html. Retrieved 2018-08-14.
- ↑ 3.0 3.1 3.2 Friedrich, B.; Herschbach, D. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today 56 (12): 53. doi:10.1063/1.1650229. Bibcode: 2003PhT....56l..53F.
- ↑ Castelvecchi, D. (2022). "The Stern–Gerlach experiment at 100". Nature Reviews Physics 4 (3): 140–142. doi:10.1038/s42254-022-00436-4. Bibcode: 2022NatRP...4..140C. https://doi.org/10.1038/s42254-022-00436-4.
- ↑ Gerlach, W.; Stern, O. (1922). "Das magnetische Moment des Silberatoms". Zeitschrift für Physik 9 (1): 353–355. doi:10.1007/BF01326984. Bibcode: 1922ZPhy....9..353G.
- ↑ Gerlach, W.; Stern, O. (1922). "Der experimentelle Nachweis des magnetischen Moments des Silberatoms". Zeitschrift für Physik 8 (1): 110–111. doi:10.1007/BF01329580. Bibcode: 1922ZPhy....8..110G. https://zenodo.org/record/1525119.
- ↑ Mott, N.F., Massey, H.S.W. (1965/1971). The Theory of Atomic Collisions, third edition, Oxford University Press, Oxford UK, pp. 214–219, §2, Ch. IX, reprinted in Wheeler, J.A.; Zurek, W.H. (1983). Quantum Theory and Measurement. Princeton NJ: Princeton University Press. pp. 701–706.
- ↑ George H. Rutherford and Rainer Grobe (1997). "Comment on "Stern-Gerlach Effect for Electron Beams"". Phys. Rev. Lett. 81 (4772): 4772. doi:10.1103/PhysRevLett.81.4772. Bibcode: 1998PhRvL..81.4772R.
- ↑ 9.0 9.1 Sakurai, J.-J. (1985). Modern quantum mechanics. Addison-Wesley. ISBN 0-201-53929-2.
- ↑ 10.0 10.1 10.2 Qinxun, Li (June 8, 2020). "Stern Gerlach Experiment:Descriptions and Developments". University of Science and Technology of China: 2–5. http://home.ustc.edu.cn/~liqinxun/Intro_to_SGE.pdf. Retrieved 24 November 2020.
- ↑ Castelvecchi, Davide (2020). "Just a moment". Nature Physics 16 (9): 994. doi:10.1038/s41567-020-1022-6. Bibcode: 2020NatPh..16..994C.
- ↑ Kragh, Helge (2012). "The Bohr–Sommerfeld theory". Niels Bohr and the quantum atom: The Bohr model of atomic structure 1913–1925. Oxford University Press. pp. 140–181. doi:10.1093/acprof:oso/9780199654987.003.0004. ISBN 978-0-19-965498-7. https://doi.org/10.1093/acprof:oso/9780199654987.003.0004.
- ↑ Stern, O. (1921). "Ein Weg zur experimentellen Pruefung der Richtungsquantelung im Magnetfeld". Zeitschrift für Physik 7 (1): 249–253. doi:10.1007/BF01332793. Bibcode: 1921ZPhy....7..249S.
- ↑ Eisberg, Robert; Resnick, Robert (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei, and Particles (2nd ed.). Wiley. p. 277. ISBN 9780471873730. https://archive.org/details/quantumphysicsat00eisb.
- ↑ Weinert, F. (1995). "Wrong theory—right experiment: The significance of the Stern–Gerlach experiments". Studies in History and Philosophy of Modern Physics 26B (1): 75–86. doi:10.1016/1355-2198(95)00002-B. Bibcode: 1995SHPMP..26...75W.
- ↑ Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review 29 (2): 309–320. doi:10.1103/PhysRev.29.309. Bibcode: 1927PhRv...29..309P.
- ↑ A., Henok (2002). Introduction to Applied Modern Physics. Lulu.com. p. 76. ISBN 1-4357-0521-1.[self-published source]
- ↑ French, A.P., Taylor, E.F. (1979). An Introduction to Quantum Physics, Van Nostrand Reinhold, London, ISBN:0-442-30770-5, pp. 428–442.
- ↑ Griffiths, David (2005). Introduction to Quantum Mechanics, 2nd ed.. Pearson Prentice Hall. p. 267. ISBN 0-13-111892-7.
- ↑ Bohm, David (1951). Quantum Theory. New York: Prentice-Hall. pp. 326–330.
- ↑ Gottfried, Kurt (1966). Quantum Mechanics. New York: W. A. Benjamin, Inc.. pp. 170–174.
- ↑ Eisberg, Robert (1961). Fundamentals of Modern Physics. New York: John Wiley & Sons. pp. 334–338. ISBN 0-471-23463-X.
- ↑ Devereux, Michael (2015). "Reduction of the atomic wave function in the Stern–Gerlach magnetic field". Canadian Journal of Physics 93 (11): 1382–1390. doi:10.1139/cjp-2015-0031. ISSN 0008-4204. Bibcode: 2015CaJPh..93.1382D.
Further reading
- Devereux, M. (2015). "Reduction of the atomic wavefunction in the Stern-Gerlach magnetic field". Canadian Journal of Physics 93 (11): 1382–1390. doi:10.1139/cjp-2015-0031. Bibcode: 2015CaJPh..93.1382D.
- Michael Devereux - Reduction of the atomic wavefunction in the Stern-Gerlach magnetic field
- Friedrich, B.; Herschbach, D. (2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics". Physics Today 56 (12): 53. doi:10.1063/1.1650229. Bibcode: 2003PhT....56l..53F.
- Reinisch, G. (1999). "Stern–Gerlach experiment as the pioneer—and probably the simplest—quantum entanglement test?". Physics Letters A 259 (6): 427–430. doi:10.1016/S0375-9601(99)00472-7. Bibcode: 1999PhLA..259..427R.
- Venugopalan, A. (1997). "Decoherence and Schrödinger-cat states in a Stern−Gerlach-type experiment". Physical Review A 56 (5): 4307–4310. doi:10.1103/PhysRevA.56.4307. Bibcode: 1997PhRvA..56.4307V.
- Hsu, B.; Berrondo, M.; Van Huele, J.-F. (2011). "Stern-Gerlach dynamics with quantum propagators". Physical Review A 83 (1): 012109–1–12. doi:10.1103/PhysRevA.83.012109. Bibcode: 2011PhRvA..83a2109H. https://zenodo.org/record/894868.
- Jeremy Bernstein (2010). "The Stern Gerlach Experiment". arXiv:1007.2435v1 [physics.hist-ph].
- The (Often) Overlooked Experiment That Revealed the Quantum World
External links
- The Stern-Gerlach experiment - Feynman Lectures on Physics
- Stern–Gerlach Experiment Java Applet Animation
- Stern–Gerlach Experiment Flash Model
- Detailed explanation of the Stern–Gerlach Experiment
- Right experiment, wrong theory: The Stern-Gerlach experiment at plato.stanford.edu
- Animation, applications and research linked to the spin (Université Paris Sud)
 |