Physics:Introduction to quantum mechanics
| Part of a series on |
| Quantum mechanics |
|---|
| [math]\displaystyle{ i \hbar \frac{\partial}{\partial t} | \psi (t) \rangle = \hat{H} | \psi (t) \rangle }[/math] |
Quantum mechanics is the study of matter and its interactions with energy on the scale of atomic and subatomic particles. By contrast, classical physics explains matter and energy only on a scale familiar to human experience, including the behavior of astronomical bodies such as the moon. Classical physics is still used in much of modern science and technology. However, towards the end of the 19th century, scientists discovered phenomena in both the large (macro) and the small (micro) worlds that classical physics could not explain.[1] The desire to resolve inconsistencies between observed phenomena and classical theory led to a revolution in physics, a shift in the original scientific paradigm:[2] the development of quantum mechanics.
Many aspects of quantum mechanics are counterintuitive[3] and can seem paradoxical because they describe behavior quite different from that seen at larger scales. In the words of quantum physicist Richard Feynman, quantum mechanics deals with "nature as She is—absurd".[4] Features of quantum mechanics often defy simple explanations in everyday language. One example of this is the uncertainty principle: precise measurements of position cannot be combined with precise measurements of velocity. Another example is entanglement. In certain circumstances, two particles with a shared history may become mutually 'entangled', in which case a measurement made on one particle (such as an electron that is measured to have spin up) will be statistically correlated with the outcome of an equivalent measurement on the other particle (that the other will be more likely to be found to have spin down). This applies even though the particles may be so far apart that it is impossible for the result of the first measurement to have been transmitted to the second particle before the second measurement takes place.
Quantum mechanics helps us understand chemistry, because it explains how atoms interact with each other and form molecules. Many remarkable phenomena can be explained using quantum mechanics, like superfluidity. Liquid helium in a container, cooled to a temperature near absolute zero spontaneously flows up and over the rim of its container, an effect which cannot be explained by classical physics.
History
Maxwell's unification of electricity, magnetism, and light in the 1880s led to experiments on the interaction of light and matter. Some of these experiments had aspects which could not be explained. Quantum mechanics emerged in the early part of the 20th century from efforts to explain these results.[5]
Evidence of quanta from the photoelectric effect
The seeds of the quantum revolution appear in the discovery by JJ Thomson in 1897 that cathode rays were not continuous but "corpuscles" now called electrons. Electrons had been named just six years earlier as part of the emerging theory of atoms. In 1900, Max Planck, a conservative physicist unconvinced by the atomic theory, discovered that he needed discrete entities like atoms or electrons to explain blackbody radiation.[6]
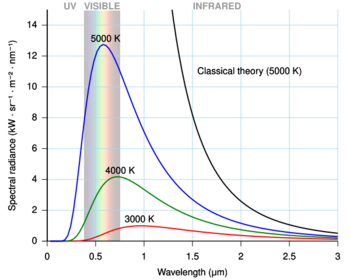
Hot objects radiate heat; very hot objects – red hot, white hot objects – all look similar when heated to the same temperature. This temperature dependent "look" results from a common curve of light intensity at different frequencies (colors). The common curve is called blackbody radiation. The lowest frequencies are invisible heat rays – infrared light. White hot objects have intensity across many colors in the visible range. Continuous wave theories of light and matter cannot explain the blackbody radiation curve. Planck spread the heat energy among individual "oscillators" of an undefined character but with discrete energy capacity: the blackbody radiation behavior was then predicted by this model.
At the time, electrons, atoms, and discrete oscillators were all exotic ideas to explain exotic phenomena. But in 1905 Albert Einstein proposed that light was also corpuscular, consisting of "energy quanta", seemingly in contradiction to the established science of light as a continuous wave, stretching back a hundred years to Thomas Young's work on diffraction.
His revolutionary proposal started by reanalyzing Planck blackbody theory, arriving at the same conclusions by using the new "energy quanta". Einstein then showed how energy quanta connected to JJ Thomson's electron. In 1902, Philipp Lenard directed light from an arc lamp onto freshly cleaned metal plates housed in an evacuated glass tube. He measured the electric current coming off the metal plate, for higher and lower intensity of light and for different metals. This is the photoelectric effect. Lenard showed that amount of current – the number of electrons – depended on the intensity of the light, but that the velocity of these electrons did not depend on intensity. The continuous wave theories of the time would predict that more light intensity would accelerate the same amount of current to higher velocity contrary to experiment. Einstein's energy quanta explained the volume increase: one electron is ejected for each quantum: more quanta mean more electrons.[6]:23
Einstein then predicted that the electron velocity would increase in direct proportion to the light frequency above a fixed value that depended upon the metal. Here the idea is that energy in energy-quanta depends upon the light frequency; the energy transferred to the electron comes in proportion to the light frequency. The type of metal gives a barrier, the fixed value, that the electrons must climb over to exit their atoms, to be emitted from the metal surface and be measured.
Ten years elapsed before Millikan's definitive experiment[7] verified Einstein's prediction. During that time many scientists rejected the revolutionary idea of quanta.[8] But Planck's and Einstein's concept was in the air and soon affected other theories.
Quantization of bound electrons in atoms
Experiments with light and matter in the late 1800s uncovered a reproducible but puzzling regularity. When light was shown through purified gasses, certain frequencies (colors) did not pass. These dark absorption 'lines' followed a distinctive pattern: the gaps between the lines decreased steadily. By 1889, the Rydberg formula predicted the lines for hydrogen gas using only a constant number and the integers to index the lines.[5]:v1:376 The origin of this regularity was unknown. Solving this mystery would become first major step toward quantum mechanics.
Throughout the 19th century evidence grew for the atomic nature of matter. With JJ Thomson's discovery of the electron in 1897, scientist began the search for a model of the interior of the atom. Thomson proposed negative electrons swimming in a pool of positive charge. Between 1908 and 1911, Rutherford showed that the positive part was only 1/3000th of the diameter of the atom.[6]:26
Models of "planetary" electrons orbiting a nuclear "Sun" were proposed, but cannot explain why the electron does not simply fall into the positive charge. In 1913 Niels Bohr and Ernest Rutherford connected the new atom models to the mystery of the Rydberg formula: the orbital radius of the electrons were constrained and the resulting energy differences matched the energy differences in the absorption lines. This meant that absorption and emission of light from atoms was energy quantized: only specific energies that matched the difference in orbital energy would be emitted or absorbed.[6]:31
Trading one mystery – the regular pattern of the Rydberg formula – for another mystery – constraints on electron orbits – might not seem like a big advance, but the new atom model summarized many other experimental findings. The quantization of the photoelectric effect and now the quantization of the electron orbits set the stage for the final revolution.
Quantization of spin
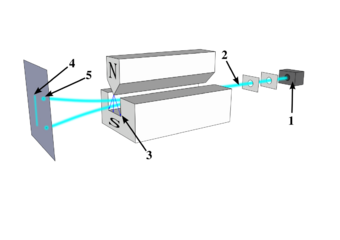
In 1922 Otto Stern and Walther Gerlach demonstrated that the magnetic properties of silver atoms defy classical explanation. They fired a beam of silver atoms through a magnetic field. According to classical physics, the atoms should have emerged in a spray, with a continuous range of directions. Instead, the beam separated into two, and only two, diverging streams of atoms.[9] Unlike the other quantum effects known at the time, this striking result involves the state of a single atom.[5]:v2:130 In 1927, T.E. Phipps and J.B. Taylor obtained a similar, but less pronounced effect using hydrogen atoms in their ground state, thereby eliminating any doubts that may have been caused by the use of silver atoms.[10]
In 1924, Wolfgang Pauli called it "two-valuedness not describable classically" and associated it with electrons in the outermost shell.[11] The experiments lead to formulation of its theory described to arise from spin of the electron in 1925, by Samuel Goudsmit and George Uhlenbeck, under the advice of Paul Ehrenfest.[12]
Quantization of matter
Max Born's 1924 paper "Zur Quantenmechanik" was the first use of the words "quantum mechanics" in print.[13][14] His later work included developing quantum collision models; in a footnote to a 1926 paper he proposed the Born rule connecting theoretical models to experiment.[15]
In 1927 at Bell Labs, Clinton Davisson and Lester Germer fired slow-moving electrons at a crystalline nickel target which showed a diffraction pattern[16][17][18][19] indicating wave nature of electron whose theory was fully explained by Hans Bethe.[20] A similar experiment by George Paget Thomson and Alexander Reid, firing electrons at thin celluloid foils and later metal films, observing rings independently discovered matter wave nature of electrons.[21]
Further Developments
In 1928 Paul Dirac published his relativistic wave equation simultaneously incorporating relativity, predicting anti-matter, and providing a complete theory for the Stern–Gerlach result.[6]:131 These successes launched a new fundamental understanding of our world at small scale: quantum mechanics.
Planck and Einstein started the revolution with quanta that broke down the continuous models of matter and light. Twenty years later "corpuscles" like electrons came to be modeled as continuous waves. This result came to be called wave-particle duality, one iconic idea along with the uncertainty principle that sets quantum mechanics apart from older models of physics.
Quantum radiation, quantum fields
In 1923 Compton demonstrated that the Planck-Einstein energy quanta from light also had momentum; three years later the "energy quanta" got a new name "photon"[22] Despite its role in almost all stages of the quantum revolution, no explicit model for light quanta existed until 1927 when Paul Dirac began work on a quantum theory of radiation[23] that became quantum electrodynamics. Over the following decades this work evolved into quantum field theory, the basis for modern quantum optics and particle physics.
Correspondence principle
Throughout the first and the modern era of quantum mechanics the concept that classical mechanics must be valid macroscopically constrained possible quantum models. This concept was formalized by Bohr in 1923 as the correspondence principle. It requires quantum theory to converge to classical limits.[24]: 29
One principal "paradox" is the apparent inconsistency between Newton's laws and quantum mechanics which can be explained using Ehrenfest's theorem, which shows that the average values obtained from quantum mechanics (e.g. position and momentum) obey classical laws.[25] However, Ehrenfest's theorem is far from capable of explaining all the counterintuitive phenomena (quantum weirdness) that have been observed, but rather is a mathematical expression of the correspondence principle.
Wave–particle duality
The concept of wave–particle duality says that neither the classical concept of "particle" nor of "wave" can fully describe the behavior of quantum-scale objects, either photons or matter. Wave–particle duality is an example of the principle of complementarity in quantum physics.[26][27][28][29][30] An elegant example of wave-particle duality is the double-slit experiment.
File:Wave-particle duality.ogv In the double-slit experiment, as originally performed by Thomas Young in 1803,[31] and then Augustin Fresnel a decade later,[31] a beam of light is directed through two narrow, closely spaced slits, producing an interference pattern of light and dark bands on a screen. If one of the slits is covered up, one might naïvely expect that the intensity of the fringes due to interference would be halved everywhere. In fact, a much simpler pattern is seen, a diffraction pattern diametrically opposite the open slit. The same behavior can be demonstrated in water waves, and so the double-slit experiment was seen as a demonstration of the wave nature of light.
Variations of the double-slit experiment have been performed using electrons, atoms, and even large molecules,[32][33] and the same type of interference pattern is seen. Thus it has been demonstrated that all matter possesses both particle and wave characteristics.
Even if the source intensity is turned down, so that only one particle (e.g. photon or electron) is passing through the apparatus at a time, the same interference pattern develops over time. The quantum particle acts as a wave when passing through the double slits, but as a particle when it is detected. This is a typical feature of quantum complementarity: a quantum particle acts as a wave in an experiment to measure its wave-like properties, and like a particle in an experiment to measure its particle-like properties. The point on the detector screen where any individual particle shows up is the result of a random process. However, the distribution pattern of many individual particles mimics the diffraction pattern produced by waves.
Uncertainty principle

Suppose it is desired to measure the position and speed of an object—for example, a car going through a radar speed trap. It can be assumed that the car has a definite position and speed at a particular moment in time. How accurately these values can be measured depends on the quality of the measuring equipment. If the precision of the measuring equipment is improved, it provides a result closer to the true value. It might be assumed that the speed of the car and its position could be operationally defined and measured simultaneously, as precisely as might be desired.
In 1927, Heisenberg proved that this last assumption is not correct.[35] Quantum mechanics shows that certain pairs of physical properties, for example, position and speed, cannot be simultaneously measured, nor defined in operational terms, to arbitrary precision: the more precisely one property is measured, or defined in operational terms, the less precisely can the other. This statement is known as the uncertainty principle. The uncertainty principle is not only a statement about the accuracy of our measuring equipment but, more deeply, is about the conceptual nature of the measured quantities—the assumption that the car had simultaneously defined position and speed does not work in quantum mechanics. On a scale of cars and people, these uncertainties are negligible, but when dealing with atoms and electrons they become critical.[36]
Heisenberg gave, as an illustration, the measurement of the position and momentum of an electron using a photon of light. In measuring the electron's position, the higher the frequency of the photon, the more accurate is the measurement of the position of the impact of the photon with the electron, but the greater is the disturbance of the electron. This is because from the impact with the photon, the electron absorbs a random amount of energy, rendering the measurement obtained of its momentum increasingly uncertain, for one is necessarily measuring its post-impact disturbed momentum from the collision products and not its original momentum (momentum which should be simultaneously measured with position). With a photon of lower frequency, the disturbance (and hence uncertainty) in the momentum is less, but so is the accuracy of the measurement of the position of the impact.[37]
At the heart of the uncertainty principle is a fact that for any mathematical analysis in the position and velocity domains, achieving a sharper (more precise) curve in the position domain can only be done at the expense of a more gradual (less precise) curve in the speed domain, and vice versa. More sharpness in the position domain requires contributions from more frequencies in the speed domain to create the narrower curve, and vice versa. It is a fundamental tradeoff inherent in any such related or complementary measurements, but is only really noticeable at the smallest (Planck) scale, near the size of elementary particles.
The uncertainty principle shows mathematically that the product of the uncertainty in the position and momentum of a particle (momentum is velocity multiplied by mass) could never be less than a certain value, and that this value is related to Planck's constant.
Wave function collapse
Wave function collapse means that a measurement has forced or converted a quantum (probabilistic or potential) state into a definite measured value. This phenomenon is only seen in quantum mechanics rather than classical mechanics.
For example, before a photon actually "shows up" on a detection screen it can be described only with a set of probabilities for where it might show up. When it does appear, for instance in the CCD of an electronic camera, the time and space where it interacted with the device are known within very tight limits. However, the photon has disappeared in the process of being captured (measured), and its quantum wave function has disappeared with it. In its place, some macroscopic physical change in the detection screen has appeared, e.g., an exposed spot in a sheet of photographic film, or a change in electric potential in some cell of a CCD.
Eigenstates and eigenvalues
Because of the uncertainty principle, statements about both the position and momentum of particles can assign only a probability that the position or momentum has some numerical value. Therefore, it is necessary to formulate clearly the difference between the state of something indeterminate, such as an electron in a probability cloud, and the state of something having a definite value. When an object can definitely be "pinned-down" in some respect, it is said to possess an eigenstate.
In the Stern–Gerlach experiment discussed above, the spin of the atom about the vertical axis has two eigenstates: up and down. Before measuring it, we can only say that any individual atom has an equal probability of being found to have spin up or spin down. The measurement process causes the wave function to collapse into one of the two states.
The eigenstates of spin about the vertical axis are not simultaneously eigenstates of spin about the horizontal axis, so this atom has an equal probability of being found to have either value of spin about the horizontal axis. As described in the section above, measuring the spin about the horizontal axis can allow an atom that was spun up to spin down: measuring its spin about the horizontal axis collapses its wave function into one of the eigenstates of this measurement, which means it is no longer in an eigenstate of spin about the vertical axis, so can take either value.
The Pauli exclusion principle
In 1924, Wolfgang Pauli proposed a new quantum degree of freedom (or quantum number), with two possible values, to resolve inconsistencies between observed molecular spectra and the predictions of quantum mechanics. In particular, the spectrum of atomic hydrogen had a doublet, or pair of lines differing by a small amount, where only one line was expected. Pauli formulated his exclusion principle, stating, "There cannot exist an atom in such a quantum state that two electrons within [it] have the same set of quantum numbers."[38]
A year later, Uhlenbeck and Goudsmit identified Pauli's new degree of freedom with the property called spin whose effects were observed in the Stern–Gerlach experiment.
Dirac wave equation
In 1928, Paul Dirac extended the Pauli equation, which described spinning electrons, to account for special relativity. The result was a theory that dealt properly with events, such as the speed at which an electron orbits the nucleus, occurring at a substantial fraction of the speed of light. By using the simplest electromagnetic interaction, Dirac was able to predict the value of the magnetic moment associated with the electron's spin and found the experimentally observed value, which was too large to be that of a spinning charged sphere governed by classical physics. He was able to solve for the spectral lines of the hydrogen atom and to reproduce from physical first principles Sommerfeld's successful formula for the fine structure of the hydrogen spectrum.
Dirac's equations sometimes yielded a negative value for energy, for which he proposed a novel solution: he posited the existence of an antielectron and a dynamical vacuum. This led to the many-particle quantum field theory.
Quantum entanglement
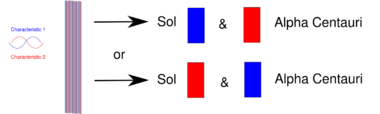
The Pauli exclusion principle says that two electrons in one system cannot be in the same state. Nature leaves open the possibility, however, that two electrons can have both states "superimposed" over each of them. Recall that the wave functions that emerge simultaneously from the double slits arrive at the detection screen in a state of superposition. Nothing is certain until the superimposed waveforms "collapse". At that instant, an electron shows up somewhere in accordance with the probability that is the square of the absolute value of the sum of the complex-valued amplitudes of the two superimposed waveforms. The situation there is already very abstract. A concrete way of thinking about entangled photons, photons in which two contrary states are superimposed on each of them in the same event, is as follows:
Imagine that we have two color-coded states of photons: one state labeled blue and another state labeled red. Let the superposition of the red and the blue state appear (in imagination) as a purple state. We consider a case in which two photons are produced as the result of one single atomic event. Perhaps they are produced by the excitation of a crystal that characteristically absorbs a photon of a certain frequency and emits two photons of half the original frequency. In this case, the photons are interconnected via their shared origin in a single atomic event. This setup results in superimposed states of the photons. So the two photons come out purple. If the experimenter now performs some experiment that determines whether one of the photons is either blue or red, then that experiment changes the photon involved from one having a superposition of blue and red characteristics to a photon that has only one of those characteristics. The problem that Einstein had with such an imagined situation was that if one of these photons had been kept bouncing between mirrors in a laboratory on earth, and the other one had traveled halfway to the nearest star when its twin was made to reveal itself as either blue or red, that meant that the distant photon now had to lose its purple status too. So whenever it might be investigated after its twin had been measured, it would necessarily show up in the opposite state to whatever its twin had revealed.
In trying to show that quantum mechanics was not a complete theory, Einstein started with the theory's prediction that two or more particles that have interacted in the past can appear strongly correlated when their various properties are later measured. He sought to explain this seeming interaction classically, through their common past, and preferably not by some "spooky action at a distance". The argument is worked out in a famous paper, Einstein, Podolsky, and Rosen (1935; abbreviated EPR) setting out what is now called the EPR paradox. Assuming what is now usually called local realism, EPR attempted to show from quantum theory that a particle has both position and momentum simultaneously, while according to the Copenhagen interpretation, only one of those two properties actually exists and only at the moment that it is being measured. EPR concluded that quantum theory is incomplete in that it refuses to consider physical properties that objectively exist in nature. (Einstein, Podolsky, & Rosen 1935 is currently Einstein's most cited publication in physics journals.) In the same year, Erwin Schrödinger used the word "entanglement" and declared: "I would not call that one but rather the characteristic trait of quantum mechanics."[39] The Irish physicist John Stewart Bell carried the analysis of quantum entanglement much further. He deduced that if measurements are performed independently on the two separated particles of an entangled pair, then the assumption that the outcomes depend upon hidden variables within each half implies a mathematical constraint on how the outcomes on the two measurements are correlated. This constraint would later be named the Bell inequality. Bell then showed that quantum physics predicts correlations that violate this inequality. Consequently, the only way that hidden variables could explain the predictions of quantum physics is if they are "nonlocal", which is to say that somehow the two particles are able to interact instantaneously no matter how widely they ever become separated.[40][41] Performing experiments like those that Bell suggested, physicists have found that nature obeys quantum mechanics and violates Bell inequalities. In other words, the results of these experiments are incompatible with any local hidden variable theory.[42][43]
Quantum field theory
The idea of quantum field theory began in the late 1920s with British physicist Paul Dirac, when he attempted to quantize the energy of the electromagnetic field; just like in quantum mechanics the energy of an electron in the hydrogen atom was quantized. Quantization is a procedure for constructing a quantum theory starting from a classical theory.
Merriam-Webster defines a field in physics as "a region or space in which a given effect (such as magnetism) exists".[44] Other effects that manifest themselves as fields are gravitation and static electricity.[45] In 2008, physicist Richard Hammond wrote:
Sometimes we distinguish between quantum mechanics (QM) and quantum field theory (QFT). QM refers to a system in which the number of particles is fixed, and the fields (such as the electromechanical field) are continuous classical entities. QFT ... goes a step further and allows for the creation and annihilation of particles ...
He added, however, that quantum mechanics is often used to refer to "the entire notion of quantum view".[46]:108
In 1931, Dirac proposed the existence of particles that later became known as antimatter.[47] Dirac shared the Nobel Prize in Physics for 1933 with Schrödinger "for the discovery of new productive forms of atomic theory".[48]
Quantum electrodynamics
Quantum electrodynamics (QED) is the name of the quantum theory of the electromagnetic force. Understanding QED begins with understanding electromagnetism. Electromagnetism can be called "electrodynamics" because it is a dynamic interaction between electrical and magnetic forces. Electromagnetism begins with the electric charge.
Electric charges are the sources of and create, electric fields. An electric field is a field that exerts a force on any particles that carry electric charges, at any point in space. This includes the electron, proton, and even quarks, among others. As a force is exerted, electric charges move, a current flows, and a magnetic field is produced. The changing magnetic field, in turn, causes electric current (often moving electrons). The physical description of interacting charged particles, electrical currents, electrical fields, and magnetic fields is called electromagnetism.
In 1928 Paul Dirac produced a relativistic quantum theory of electromagnetism. This was the progenitor to modern quantum electrodynamics, in that it had essential ingredients of the modern theory. However, the problem of unsolvable infinities developed in this relativistic quantum theory. Years later, renormalization largely solved this problem. Initially viewed as a provisional, suspect procedure by some of its originators, renormalization eventually was embraced as an important and self-consistent tool in QED and other fields of physics. Also, in the late 1940s Feynman diagrams provided a way to make predictions with QED by finding a probability amplitude for each possible way that an interaction could occur. The diagrams showed in particular that the electromagnetic force is the exchange of photons between interacting particles.[49]
The Lamb shift is an example of a quantum electrodynamics prediction that has been experimentally verified. It is an effect whereby the quantum nature of the electromagnetic field makes the energy levels in an atom or ion deviate slightly from what they would otherwise be. As a result, spectral lines may shift or split.
Similarly, within a freely propagating electromagnetic wave, the current can also be just an abstract displacement current, instead of involving charge carriers. In QED, its full description makes essential use of short-lived virtual particles. There, QED again validates an earlier, rather mysterious concept.
Standard Model
The Standard Model of particle physics is the quantum field theory that describes three of the four known fundamental forces (electromagnetic, weak and strong interactions – excluding gravity) in the universe and classifies all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.
Although the Standard Model is believed to be theoretically self-consistent and has demonstrated success in providing experimental predictions, it leaves some physical phenomena unexplained and so falls short of being a complete theory of fundamental interactions. For example, it does not fully explain baryon asymmetry, incorporate the full theory of gravitation as described by general relativity, or account for the universe's accelerating expansion as possibly described by dark energy. The model does not contain any viable dark matter particle that possesses all of the required properties deduced from observational cosmology. It also does not incorporate neutrino oscillations and their non-zero masses. Accordingly, it is used as a basis for building more exotic models that incorporate hypothetical particles, extra dimensions, and elaborate symmetries (such as supersymmetry) to explain experimental results at variance with the Standard Model, such as the existence of dark matter and neutrino oscillations.
Interpretations
The physical measurements, equations, and predictions pertinent to quantum mechanics are all consistent and hold a very high level of confirmation. However, the question of what these abstract models say about the underlying nature of the real world has received competing answers. These interpretations are widely varying and sometimes somewhat abstract. For instance, the Copenhagen interpretation states that before a measurement, statements about a particle's properties are completely meaningless, while in the many-worlds interpretation describes the existence of a multiverse made up of every possible universe.[50]
Light behaves in some aspects like particles and in other aspects like waves. Matter—the "stuff" of the universe consisting of particles such as electrons and atoms—exhibits wavelike behavior too. Some light sources, such as neon lights, give off only certain specific frequencies of light, a small set of distinct pure colors determined by neon's atomic structure. Quantum mechanics shows that light, along with all other forms of electromagnetic radiation, comes in discrete units, called photons, and predicts its spectral energies (corresponding to pure colors), and the intensities of its light beams. A single photon is a quantum, or smallest observable particle, of the electromagnetic field. A partial photon is never experimentally observed. More broadly, quantum mechanics shows that many properties of objects, such as position, speed, and angular momentum, that appeared continuous in the zoomed-out view of classical mechanics, turn out to be (in the very tiny, zoomed-in scale of quantum mechanics) quantized. Such properties of elementary particles are required to take on one of a set of small, discrete allowable values, and since the gap between these values is also small, the discontinuities are only apparent at very tiny (atomic) scales.
Applications
Everyday applications
The relationship between the frequency of electromagnetic radiation and the energy of each photon is why ultraviolet light can cause sunburn, but visible or infrared light cannot. A photon of ultraviolet light delivers a high amount of energy—enough to contribute to cellular damage such as occurs in a sunburn. A photon of infrared light delivers less energy—only enough to warm one's skin. So, an infrared lamp can warm a large surface, perhaps large enough to keep people comfortable in a cold room, but it cannot give anyone a sunburn.[51]
Technological applications
Applications of quantum mechanics include the laser, the transistor, the electron microscope, and magnetic resonance imaging. A special class of quantum mechanical applications is related to macroscopic quantum phenomena such as superfluid helium and superconductors. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
In even the simple light switch, quantum tunneling is absolutely vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up of a layer of oxide. Flash memory chips found in USB drives also use quantum tunneling, to erase their memory cells.[52]
See also
- Einstein's thought experiments
- Macroscopic quantum phenomena
- Philosophy of physics
- Quantum computing
- Virtual particle
- Teaching quantum mechanics
- List of textbooks on classical and quantum mechanics
Notes
References
- ↑ "Quantum Mechanics". National Public Radio. https://www.pbs.org/transistor/science/info/quantum.html.
- ↑ Kuhn, Thomas S. The Structure of Scientific Revolutions. Fourth ed. Chicago; London: The University of Chicago Press, 2012. Print.
- ↑ "Introduction to Quantum Mechanics". https://www.socratease.in/chapters/intro/intro-to-quantum-mechanics-1.
- ↑ Feynman, Richard P. (1988). QED : the strange theory of light and matter (1st Princeton pbk., seventh printing with corrections. ed.). Princeton, NJ: Princeton University Press. pp. 10. ISBN 978-0691024172. https://archive.org/details/qedstrangetheory00feyn/page/10.
- ↑ Jump up to: 5.0 5.1 5.2 Whittaker, Edmund T. (1989). A history of the theories of aether & electricity. 2: The modern theories, 1900 – 1926 (Repr ed.). New York: Dover Publ. ISBN 978-0-486-26126-3.
- ↑ Jump up to: 6.0 6.1 6.2 6.3 6.4 Baggott, J. E. (2013). The quantum story: a history in 40 moments (Impression: 3 ed.). Oxford: Oxford Univ. Press. ISBN 978-0-19-965597-7.
- ↑ Millikan, R. A. (1916-03-01). "A Direct Photoelectric Determination of Planck's " h "" (in en). Physical Review 7 (3): 355–388. doi:10.1103/PhysRev.7.355. ISSN 0031-899X. Bibcode: 1916PhRv....7..355M. https://link.aps.org/doi/10.1103/PhysRev.7.355.
- ↑ Pais, A. (1979-10-01). "Einstein and the quantum theory" (in en). Reviews of Modern Physics 51 (4): 863–914. doi:10.1103/RevModPhys.51.863. ISSN 0034-6861. Bibcode: 1979RvMP...51..863P. https://link.aps.org/doi/10.1103/RevModPhys.51.863.
- ↑ Friedrich, Bretislav; Herschbach, Dudley (December 2003). "Stern and Gerlach: How a Bad Cigar Helped Reorient Atomic Physics" (in en). Physics Today 56 (12): 53–59. doi:10.1063/1.1650229. ISSN 0031-9228. Bibcode: 2003PhT....56l..53F.
- ↑ Phipps, T.E.; Taylor, J.B. (1927). "The Magnetic Moment of the Hydrogen Atom". Physical Review 29 (2): 309–320. doi:10.1103/PhysRev.29.309. Bibcode: 1927PhRv...29..309P.
- ↑ Wolfgang Pauli (December 13, 1946). "Exclusion Principle and Quantum Mechanics". Nobel Lecture. Nobel Prize. https://www.nobelprize.org/prizes/physics/1945/pauli/lecture/.
- ↑ Ehrenfest, P. (November 1925). "Ersetzung der Hypothese vom unmechanischen Zwang durch eine Forderung bezüglich des inneren Verhaltens jedes einzelnen Elektrons" (in de). Die Naturwissenschaften 13 (47): 953–954. doi:10.1007/bf01558878. ISSN 0028-1042.
- ↑ Max Born, My Life: Recollections of a Nobel Laureate, Taylor & Francis, London, 1978. ("We became more and more convinced that a radical change of the foundations of physics was necessary, i.e., a new kind of mechanics for which we used the term quantum mechanics. This word appears for the first time in physical literature in a paper of mine...")
- ↑ Fedak, William A.; Prentis, Jeffrey J. (2009-02-01). "The 1925 Born and Jordan paper "On quantum mechanics"" (in en). American Journal of Physics 77 (2): 128–139. doi:10.1119/1.3009634. ISSN 0002-9505. Bibcode: 2009AmJPh..77..128F. https://people.isy.liu.se/icg/jalar/kurser/QF/references/onBornJordan1925.pdf.
- ↑ Born, Max (1926). "Zur Quantenmechanik der Stoßvorgänge". Zeitschrift für Physik 37 (12): 863–867. doi:10.1007/BF01397477. Bibcode: 1926ZPhy...37..863B. Reprinted as Born, Max (1983). "On the quantum mechanics of collisions". in Wheeler, J. A.; Zurek, W. H.. Quantum Theory and Measurement. Princeton University Press. pp. 52–55. ISBN 978-0-691-08316-2.
- ↑ Davisson, C.; Germer, L. H. (1927). "Diffraction of Electrons by a Crystal of Nickel". Physical Review 30 (6): 705–740. doi:10.1103/physrev.30.705. ISSN 0031-899X. Bibcode: 1927PhRv...30..705D.
- ↑ Davisson, C. J.; Germer, L. H. (1928). "Reflection of Electrons by a Crystal of Nickel" (in en). Proceedings of the National Academy of Sciences 14 (4): 317–322. doi:10.1073/pnas.14.4.317. ISSN 0027-8424. PMID 16587341. Bibcode: 1928PNAS...14..317D.
- ↑ Davisson, C.; Germer, L. H. (1927). "The Scattering of Electrons by a Single Crystal of Nickel". Nature 119 (2998): 558–560. doi:10.1038/119558a0. ISSN 0028-0836. http://dx.doi.org/10.1038/119558a0.
- ↑ Davisson, C. J.; Germer, L. H. (1928). "Reflection and Refraction of Electrons by a Crystal of Nickel" (in en). Proceedings of the National Academy of Sciences 14 (8): 619–627. doi:10.1073/pnas.14.8.619. ISSN 0027-8424. PMID 16587378. Bibcode: 1928PNAS...14..619D.
- ↑ Bethe, H. (1928). "Theorie der Beugung von Elektronen an Kristallen" (in de). Annalen der Physik 392 (17): 55–129. doi:10.1002/andp.19283921704. Bibcode: 1928AnP...392...55B. https://onlinelibrary.wiley.com/doi/10.1002/andp.19283921704.
- ↑ Thomson, G. P.; Reid, A. (1927). "Diffraction of Cathode Rays by a Thin Film" (in en). Nature 119 (3007): 890. doi:10.1038/119890a0. ISSN 0028-0836. Bibcode: 1927Natur.119Q.890T.
- ↑ ."December 18, 1926: Gilbert Lewis coins "photon" in letter to Nature" (in en). https://www.aps.org/publications/apsnews/201212/physicshistory.cfm.
- ↑ Dirac, P. A. M. (1927-03-01). "The quantum theory of the emission and absorption of radiation" (in en). Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 114 (767): 243–265. doi:10.1098/rspa.1927.0039. ISSN 0950-1207. Bibcode: 1927RSPSA.114..243D.
- ↑ Messiah, Albert (1966) (in en). Quantum Mechanics. North Holland, John Wiley & Sons. ISBN 0486409244.
- ↑ "Remarks concerning the status & some ramifications of EHRENFEST'S THEOREM". https://www.reed.edu/physics/faculty/wheeler/documents/Quantum%20Mechanics/Miscellaneous%20Essays/Ehrenfest's%20Theorem.pdf.
- ↑ Zettili, Nouredine (2009). Quantum Mechanics: Concepts and Applications. John Wiley and Sons. pp. 26–27. ISBN 978-0470026786. https://books.google.com/books?id=6jXlpJCSz98C&q=%22complementarity+principle%22+%22wave-particle+duality%22&pg=PA26.
- ↑ Selleri, Franco (2012). Wave-Particle Duality. Springer Science and Business Media. pp. 41. ISBN 978-1461533320. https://books.google.com/books?id=r8bkBwAAQBAJ&q=%22complementarity+principle%22+%22wave-particle+duality%22&pg=PA41.
- ↑ Podgorsak, Ervin B. (2013). Compendium to Radiation Physics for Medical Physicists. Springer Science and Business Media. pp. 88. ISBN 978-3642201868. https://books.google.com/books?id=7zfBBAAAQBAJ&q=%22complementarity+principle%22+%22wave-particle+duality%22&pg=PA88.
- ↑ Halliday, David; Resnick, Robert (2013). Fundamentals of Physics, 10th Ed.. John Wiley and Sons. pp. 1272. ISBN 978-1118230619. https://books.google.com/books?id=nQZyAgAAQBAJ&q=%22complementarity+principle%22+%22wave-particle+duality%22&pg=SL9-PA21.
- ↑ Myers, Rusty L. (2006). The Basics of Physics. Greenwood Publishing Group. pp. 172. ISBN 0313328579. https://archive.org/details/basicsofphysics0000myer. "complementarity principle wave-particle duality."
- ↑ Jump up to: 31.0 31.1 Shamos, Morris H (1 January 1987). Great Experiments in Physics: Firsthand Accounts from Galileo to Einstein. Courier Corporation. p. 108.
- ↑ Merali, Zeeya (21 May 2015). "Quantum physics: What is really real?". Nature 521 (7552): 278–80. doi:10.1038/521278a. PMID 25993941. Bibcode: 2015Natur.521..278M.
- ↑ Eibenberger, Sandra (2013). "Matter–wave interference of particles selected from a molecular library with masses exceeding 10 000 amu". Physical Chemistry Chemical Physics 15 (35): 14696–700. doi:10.1039/C3CP51500A. PMID 23900710. Bibcode: 2013PCCP...1514696E. "[I]n a three-grating interferometer... We observe high-contrast quantum fringe patterns of molecules... having 810 atoms in a single particle.".
- ↑ "The Nobel Prize in Physics 1932". https://www.nobelprize.org/prizes/physics/1932/summary/.
- ↑ Heisenberg first published his work on the uncertainty principle in the leading German physics journal Zeitschrift für Physik: Heisenberg, W. (1927). "Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik". Z. Phys. 43 (3–4): 172–98. doi:10.1007/BF01397280. Bibcode: 1927ZPhy...43..172H.
- ↑ "The Nobel Prize in Physics 1932". https://www.nobelprize.org/prizes/physics/1932/ceremony-speech/.
- ↑ "Uncertainty principle", Encyclopædia Britannica
- ↑ Pauling, Linus (1960). The Nature of the Chemical Bond (3rd ed.). Itahca, NY: Cornell University Press. p. 47. ISBN 0801403332. https://archive.org/details/natureofchemical0000paul_3ed. Retrieved 1 March 2016.
- ↑ E. Schrödinger, Proceedings of the Cambridge Philosophical Society, 31 (1935), p. 555, says: "When two systems, of which we know the states by their respective representation, enter into a temporary physical interaction due to known forces between them and when after a time of mutual influence the systems separate again, then they can no longer be described as before, viz., by endowing each of them with a representative of its own. I would not call that one but rather the characteristic trait of quantum mechanics."
- ↑ Parker, Sybil B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. p. 542. ISBN 978-0-07-051400-3. https://archive.org/details/mcgrawhillencycl1993park.
- ↑ Mermin, N. David (July 1993). "Hidden Variables and the Two Theorems of John Bell". Reviews of Modern Physics 65 (3): 803–15. doi:10.1103/RevModPhys.65.803. Bibcode: 1993RvMP...65..803M. http://cqi.inf.usi.ch/qic/Mermin1993.pdf.
- ↑ The BIG Bell Test Collaboration (9 May 2018). "Challenging local realism with human choices". Nature 557 (7704): 212–216. doi:10.1038/s41586-018-0085-3. PMID 29743691. Bibcode: 2018Natur.557..212B.
- ↑ Wolchover, Natalie (2017-02-07). "Experiment Reaffirms Quantum Weirdness" (in en-US). Quanta Magazine. https://www.quantamagazine.org/20170207-bell-test-quantum-loophole/.
- ↑ "Mechanics", Merriam-Webster Online Dictionary
- ↑ "Field", Encyclopædia Britannica
- ↑ Richard Hammond, The Unknown Universe, New Page Books, 2008. ISBN:978-1601630032
- ↑ "Featured Physicists – Paul Dirac 1902–1984". http://www.physicalworld.org/restless_universe/html/ru_dira.html.
- ↑ "The Nobel Prize in Physics 1933". Nobel Foundation. http://nobelprize.org/nobel_prizes/physics/laureates/1933/.
- ↑ "Exchange Particles". http://hyperphysics.phy-astr.gsu.edu/hbase/Particles/expar.html.
- ↑ "Copenhagen Interpretation". http://abyss.uoregon.edu/~js/21st_century_science/lectures/lec15.html.
- ↑ Jim Lucas: 'What Is Ultraviolet Light?', 15 September 2017, at livescience.com Accessed 27 December 2017
- ↑ Durrani, Z. A. K.; Ahmed, H. (2008). Vijay Kumar. ed. Nanosilicon. Elsevier. p. 345. ISBN 978-0080445281.
Bibliography
- Bernstein, Jeremy (2005). "Max Born and the quantum theory". American Journal of Physics 73 (11): 999–1008. doi:10.1119/1.2060717. Bibcode: 2005AmJPh..73..999B.
- Beller, Mara (2001). Quantum Dialogue: The Making of a Revolution. University of Chicago Press.
- Bohr, Niels (1958). Atomic Physics and Human Knowledge. John Wiley & Sons]. ISBN 0486479285. OCLC 530611.
- de Broglie, Louis (1953). The Revolution in Physics. Noonday Press.
- Bronner, Patrick; Strunz, Andreas; Silberhorn, Christine; Meyn, Jan-Peter (2009). "Demonstrating quantum random with single photons". European Journal of Physics 30 (5): 1189–1200. doi:10.1088/0143-0807/30/5/026. Bibcode: 2009EJPh...30.1189B.
- Einstein, Albert (1934). Essays in Science. Philosophical Library. ISBN 0486470113.
- Feigl, Herbert; Brodbeck, May (1953). Readings in the Philosophy of Science. Appleton-Century-Crofts. ISBN 0390304883. https://archive.org/details/readingsinphilos00feig.
- Feynman, Richard P. (1949). "Space-Time Approach to Quantum Electrodynamics". Physical Review 76 (6): 769–89. doi:10.1103/PhysRev.76.769. Bibcode: 1949PhRv...76..769F.
- Feynman, Richard P. (1990). QED, The Strange Theory of Light and Matter. Penguin Books. ISBN 978-0140125054.
- Fowler, Michael (1999). The Bohr Atom. University of Virginia. https://galileo.phys.virginia.edu/classes/252/Bohr_Atom/Bohr_Atom.html.[ISBN missing]
- Heisenberg, Werner (1958). Physics and Philosophy. Harper and Brothers. ISBN 0061305499. https://archive.org/details/physicsphilosoph00heis.
- Lakshmibala, S. (2004). "Heisenberg, Matrix Mechanics and the Uncertainty Principle". Resonance: Journal of Science Education 9 (8): 46–56. doi:10.1007/bf02837577.
- Liboff, Richard L. (1992). Introductory Quantum Mechanics (2nd ed.). Addison-Wesley Pub. Co.. ISBN 9780201547153. https://archive.org/details/introductoryquan00libo.[ISBN missing]
- Lindsay, Robert Bruce; Margenau, Henry (1957). Foundations of Physics. Dover. ISBN 0918024188. https://archive.org/details/foundationsofphy00lind.
- McEvoy, J. P.; Zarate, Oscar (2004). Introducing Quantum Theory. Icon Books. ISBN 1874166374. https://archive.org/details/introducingquant00mcev.
- Nave, Carl Rod (2005). "Quantum Physics". HyperPhysics. Georgia State University. http://hyperphysics.phy-astr.gsu.edu/hbase/quacon.html#quacon.
- Peat, F. David (2002). From Certainty to Uncertainty: The Story of Science and Ideas in the Twenty-First Century. Joseph Henry Press.
- Reichenbach, Hans (1944). Philosophic Foundations of Quantum Mechanics. University of California Press. ISBN 0486404595. https://archive.org/details/in.ernet.dli.2015.212027.
- Schilpp, Paul Arthur (1949). Albert Einstein: Philosopher-Scientist. Tudor Publishing Company.
- Scientific American Reader, 1953.
- Sears, Francis Weston (1949). Optics (3rd ed.). Addison-Wesley. ISBN 0195046013. https://archive.org/details/neutronopticsint0000sear.
- Shimony, A. (1983). "(title not given in citation)". Tokyo: Japan Physical Society. pp. 225.; cited in: Popescu, Sandu; Daniel Rohrlich (1996). "Action and Passion at a Distance: An Essay in Honor of Professor Abner Shimony". arXiv:quant-ph/9605004.
- Tavel, Morton; Tavel, Judith (illustrations) (2002). Contemporary physics and the limits of knowledge. Rutgers University Press. ISBN 978-0813530772. https://books.google.com/books?id=SELS0HbIhjYC&q=Wave+function+collapse&pg=PA200.
- Van Vleck, J. H.,1928, "The Correspondence Principle in the Statistical Interpretation of Quantum Mechanics", Proc. Natl. Acad. Sci. 14: 179.
- Westmoreland; Benjamin Schumacher (1998). "Quantum Entanglement and the Nonexistence of Superluminal Signals". arXiv:quant-ph/9801014.
- Wheeler, John Archibald; Feynman, Richard P. (1949). "Classical Electrodynamics in Terms of Direct Interparticle Action". Reviews of Modern Physics 21 (3): 425–33. doi:10.1103/RevModPhys.21.425. Bibcode: 1949RvMP...21..425W. https://cds.cern.ch/record/1062647/files/RevModPhys.21.425.pdf.
- Wieman, Carl; Perkins, Katherine (2005). "Transforming Physics Education". Physics Today 58 (11): 36. doi:10.1063/1.2155756. Bibcode: 2005PhT....58k..36W.
Further reading
The following titles, all by working physicists, attempt to communicate quantum theory to laypeople, using a minimum of technical apparatus.
- Jim Al-Khalili (2003). Quantum: A Guide for the Perplexed. Weidenfeld & Nicolson. ISBN:978-1780225340.
- Chester, Marvin (1987). Primer of Quantum Mechanics. John Wiley. ISBN:0486428788.
- Brian Cox and Jeff Forshaw (2011) The Quantum Universe. Allen Lane. ISBN:978-1846144325.
- Richard Feynman (1985). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN:0691083886.
- Ford, Kenneth (2005). The Quantum World. Harvard Univ. Press. Includes elementary particle physics.
- Ghirardi, GianCarlo (2004). Sneaking a Look at God's Cards, Gerald Malsbary, trans. Princeton Univ. Press. The most technical of the works cited here. Passages using algebra, trigonometry, and bra–ket notation can be passed over on a first reading.
- Tony Hey and Walters, Patrick (2003). The New Quantum Universe. Cambridge Univ. Press. Includes much about the technologies quantum theory has made possible. ISBN:978-0521564571.
- Vladimir G. Ivancevic, Tijana T. Ivancevic (2008). Quantum leap: from Dirac and Feynman, Across the universe, to human body and mind. World Scientific Publishing Company. Provides an intuitive introduction in non-mathematical terms and an introduction in comparatively basic mathematical terms. ISBN:978-9812819277.
- J. P. McEvoy and Oscar Zarate (2004). Introducing Quantum Theory. Totem Books. ISBN:1840465778'
- N. David Mermin (1990). "Spooky actions at a distance: mysteries of the QT" in his Boojums all the way through. Cambridge Univ. Press: 110–76. The author is a rare physicist who tries to communicate to philosophers and humanists. ISBN:978-0521388801.
- Roland Omnès (1999). Understanding Quantum Mechanics. Princeton Univ. Press. ISBN:978-0691004358.
- Victor Stenger (2000). Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo NY: Prometheus Books. Chpts. 5–8. ISBN:978-1573928595.
- Martinus Veltman (2003). Facts and Mysteries in Elementary Particle Physics. World Scientific Publishing Company. ISBN:978-9812381491.
External links
| The Wikibook Quantum Mechanics has a page on the topic of: Introduction to Quantum Mechanics |
- "Microscopic World – Introduction to Quantum Mechanics". by Takada, Kenjiro, emeritus professor at Kyushu University
- The Quantum Exchange (tutorials and open-source learning software).
- Atoms and the Periodic Table
- Single and double slit interference
- Time-Evolution of a Wavepacket in a Square Well An animated demonstration of a wave packet dispersion over time.
- Carroll, Sean M.. "Quantum Mechanics (an embarrassment)". Sixty Symbols. Brady Haran for the University of Nottingham. http://www.sixtysymbols.com/videos/quantum_mechanics.htm.
 |