Physics:Majorana fermion

From HandWiki
Short description: Fermion that is its own antiparticle
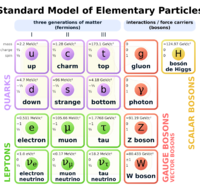
Standard Model of particle physics
Standard Model of Elementary Particles.svg
Elementary particles of the Standard Model
Background
Particle physics
Standard Model
Quantum field theory
Gauge theory
Spontaneous symmetry breaking
Higgs mechanism
Constituents
Electroweak interaction
Quantum chromodynamics
CKM matrix
Standard Model mathematics
Limitations
Strong CP problem
Hierarchy problem
Neutrino oscillations
Physics beyond the Standard Model

A Majorana fermion (/maɪəˈrɑːnə/[1]), also referred to as a Majorana particle, is a fermion that is its own antiparticle. They were hypothesised by Ettore Majorana in 1937. The term is sometimes used in opposition to a Dirac fermion, which describes fermions that are not their own antiparticles.

With the exception of neutrinos, all of the Standard Model fermions are known to behave as Dirac fermions at low energy (lower than the electroweak symmetry breaking temperature), and none are Majorana fermions. The nature of neutrinos is not settled – they may turn out to be either Dirac or Majorana fermions.

In condensed matter physics, quasiparticle excitations can appear like bound Majorana fermions. However, instead of a single fundamental particle, they are the collective movement of several individual particles (themselves composite) which are governed by non-Abelian statistics.

Theory

The concept goes back to Majorana's suggestion in 1937[2] that electrically neutral spin-1/2 particles can be described by a real-valued wave equation (the Majorana equation), and would therefore be identical to their antiparticle, because the wave functions of particle and antiparticle are related by complex conjugation, which leaves the Majorana wave equation unchanged.

The difference between Majorana fermions and Dirac fermions can be expressed mathematically in terms of the creation and annihilation operators of second quantization: The creation operator [math]\displaystyle{ \gamma^{\dagger}_j }[/math] creates a fermion in quantum state [math]\displaystyle{ j }[/math] (described by a real wave function), whereas the annihilation operator [math]\displaystyle{ \gamma_j }[/math] annihilates it (or, equivalently, creates the corresponding antiparticle). For a Dirac fermion the operators [math]\displaystyle{ \gamma^{\dagger}_j }[/math] and [math]\displaystyle{ \gamma_j }[/math] are distinct, whereas for a Majorana fermion they are identical. The ordinary fermionic annihilation and creation operators [math]\displaystyle{ f }[/math] and [math]\displaystyle{ f^{\dagger} }[/math] can be written in terms of two Majorana operators [math]\displaystyle{ \gamma_1 }[/math] and [math]\displaystyle{ \gamma_2 }[/math] by

[math]\displaystyle{ f = \tfrac{1}{\sqrt{2}} (\gamma_1+i\gamma_2), }[/math]
[math]\displaystyle{ f^{\dagger} = \tfrac{1}{\sqrt{2}} (\gamma_1-i\gamma_2) ~. }[/math]

In supersymmetry models, neutralinos – superpartners of gauge bosons and Higgs bosons – are Majorana fermions.

Identities

Another common convention for the normalization of the Majorana fermion operator is

[math]\displaystyle{ f = \tfrac{1}{2} (\gamma_1 + i\gamma_2) }[/math]
[math]\displaystyle{ f^\dagger = \tfrac{1}{2} (\gamma_1 - i\gamma_2) }[/math]

This convention has the advantage that the Majorana operator squares to the identity.

Using this convention, a collection of [math]\displaystyle{ 2n }[/math] Majorana fermions ([math]\displaystyle{ n }[/math] ordinary fermions), [math]\displaystyle{ \gamma_i }[/math] ([math]\displaystyle{ i=1,2,..,2n }[/math]) obey the following anticommutation identities

[math]\displaystyle{ \{\gamma_i,\gamma_j\} = 2 \delta_{ij} }[/math]

and

[math]\displaystyle{ \sum_{ijkl} [\gamma_i A_{ij} \gamma_j, \gamma_k B_{kl} \gamma_l] = 4 \sum_{ij} \gamma_i [A,B]_{ij} \gamma_j }[/math]

where [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are antisymmetric matrices. These are identical to the commutation relations for the real Clifford algebra in [math]\displaystyle{ n }[/math] dimensions ([math]\displaystyle{ \mathrm{Cl}( \mathbb {R}^n ) }[/math]).

Elementary particles

Because particles and antiparticles have opposite conserved charges, Majorana fermions have zero charge, hence among the fundamental particles, the only fermions that could be Majorana are sterile neutrinos, if they exist. All the other elementary fermions of the Standard Model have gauge charges, so they cannot have fundamental Majorana masses: Even the Standard Model's left-handed neutrinos and right-handed antineutrinos have non-zero weak isospin, [math]\displaystyle{ T_3 = \pm \tfrac{1}{2} , }[/math] a charge-like quantum number. However, if they exist, the so-called "sterile neutrinos" (left-handed antineutrinos and right-handed neutrinos) would be truly neutral particles (assuming no other, unknown gauge charges exist).

Ettore Majorana hypothesised the existence of Majorana fermions in 1937

The sterile neutrinos introduced to explain neutrino oscillation and anomalously small S.M. neutrino masses could have Majorana masses. If they do, then at low energy (after electroweak symmetry breaking), by the seesaw mechanism, the neutrino fields would naturally behave as six Majorana fields, with three of them expected to have very high masses (comparable to the GUT scale) and the other three expected to have very low masses (below 1 eV). If right-handed neutrinos exist but do not have a Majorana mass, the neutrinos would instead behave as three Dirac fermions and their antiparticles with masses coming directly from the Higgs interaction, like the other Standard Model fermions.

The seesaw mechanism is appealing because it would naturally explain why the observed neutrino masses are so small. However, if the neutrinos are Majorana then they violate the conservation of lepton number and even of B − L.

Neutrinoless double beta decay has not (yet) been observed,[3] but if it does exist, it can be viewed as two ordinary beta decay events whose resultant antineutrinos immediately annihilate each other, and is only possible if neutrinos are their own antiparticles.[4]

The high-energy analog of the neutrinoless double beta decay process is the production of same-sign charged lepton pairs in hadron colliders;[5] it is being searched for by both the ATLAS and CMS experiments at the Large Hadron Collider. In theories based on left–right symmetry, there is a deep connection between these processes.[6] In the currently most-favored explanation of the smallness of neutrino mass, the seesaw mechanism, the neutrino is “naturally” a Majorana fermion.

Majorana fermions cannot possess intrinsic electric or magnetic moments, only toroidal moments.[7][8][9] Such minimal interaction with electromagnetic fields makes them potential candidates for cold dark matter.[10][11]

Majorana bound states

In superconducting materials, a quasiparticle can emerge as a Majorana fermion (non-fundamental), more commonly referred to as a Bogoliubov quasiparticle in condensed matter physics. Its existence becomes possible because a quasiparticle in a superconductor is its own antiparticle.

Mathematically, the superconductor imposes electron hole "symmetry" on the quasiparticle excitations, relating the creation operator [math]\displaystyle{ \gamma(E) }[/math] at energy [math]\displaystyle{ E }[/math] to the annihilation operator [math]\displaystyle{ {\gamma^{\dagger}(-E)} }[/math] at energy [math]\displaystyle{ -E }[/math]. Majorana fermions can be bound to a defect at zero energy, and then the combined objects are called Majorana bound states or Majorana zero modes.[12] This name is more appropriate than Majorana fermion (although the distinction is not always made in the literature), because the statistics of these objects is no longer fermionic. Instead, the Majorana bound states are an example of non-abelian anyons: interchanging them changes the state of the system in a way that depends only on the order in which the exchange was performed. The non-abelian statistics that Majorana bound states possess allows them to be used as a building block for a topological quantum computer.[13]

A quantum vortex in certain superconductors or superfluids can trap midgap states, which is one source of Majorana bound states.[14][15][16] Shockley states at the end points of superconducting wires or line defects are an alternative, purely electrical, source.[17] An altogether different source uses the fractional quantum Hall effect as a substitute for the superconductor.[18]

Experiments in superconductivity

In 2008, Fu and Kane provided a groundbreaking development by theoretically predicting that Majorana bound states can appear at the interface between topological insulators and superconductors.[19][20] Many proposals of a similar spirit soon followed, where it was shown that Majorana bound states can appear even without any topological insulator. An intense search to provide experimental evidence of Majorana bound states in superconductors[21][22] first produced some positive results in 2012.[23][24] A team from the Kavli Institute of Nanoscience at Delft University of Technology in the Netherlands reported an experiment involving indium antimonide nanowires connected to a circuit with a gold contact at one end and a slice of superconductor at the other. When exposed to a moderately strong magnetic field the apparatus showed a peak electrical conductance at zero voltage that is consistent with the formation of a pair of Majorana bound states, one at either end of the region of the nanowire in contact with the superconductor.[25] Simultaneously, a group from Purdue University and University of Notre Dame reported observation of fractional Josephson effect (decrease of the Josephson frequency by a factor of 2) in indium antimonide nanowires connected to two superconducting contacts and subjected to a moderate magnetic field,[26] another signature of Majorana bound states.[27] Bound state with zero energy was soon detected by several other groups in similar hybrid devices,[28][29][30][31] and fractional Josephson effect was observed in topological insulator HgTe with superconducting contacts[32]

The aforementioned experiments mark possible verifications of independent 2010 theoretical proposals from two groups[33][34] predicting the solid state manifestation of Majorana bound states in semiconducting wires proximitized to superconductors. However, it was also pointed out that some other trivial non-topological bounded states[35] could highly mimic the zero voltage conductance peak of Majorana bound state. The subtle relation between those trivial bound states and Majorana bound states was reported by the researchers in Niels Bohr Institute,[36] who can directly "watch" coalescing Andreev bound states evolving into Majorana bound states, thanks to a much cleaner semiconductor-superconductor hybrid system.

In 2014, evidence of Majorana bound states was also observed using a low-temperature scanning tunneling microscope, by scientists at Princeton University.[37][38] These experiments resolved the predicted signatures of localized Majorana bound states – zero energy modes – at the ends of ferromagnetic (iron) chains on the surface of a superconductor (lead) with strong spin-orbit coupling. Follow up experiments at lower temperatures probed these end states with higher energy resolution and showed their robustness when the chains are buried by layers of lead.[39] Experiments with spin-polarized STM tips have also been used, in 2017, to distinguish these end modes from trivial zero energy modes that can form due to magnetic defects in a superconductor, providing important evidence (beyond zero bias peaks) for the interpretation of the zero energy mode at the end of the chains as a Majorana bound state.[40] More experiments finding evidence for Majorana bound states in chains have also been carried out with other types of magnetic chains, particularly chains manipulated atom-by-atom to make a spin helix on the surface of a superconductor.[41][42]

Majorana fermions may also emerge as quasiparticles in quantum spin liquids, and were observed by researchers at Oak Ridge National Laboratory, working in collaboration with Max Planck Institute and University of Cambridge on 4 April 2016.[43]

Chiral Majorana fermions were claimed to be detected in 2017 by Q.L. He et al., in a quantum anomalous Hall effect/superconductor hybrid device.[44][45] In this system, Majorana fermions edge mode will give a rise to a [math]\displaystyle{ \tfrac{1}{2} \tfrac{e^{2}}{h} }[/math] conductance edge current. Subsequent experiments by other groups, however, could not reproduce these findings.[46][47][48] In November 2022, the article by He et al. was retracted by the editors,[49] because "analysis of the raw and published data revealed serious irregularities and discrepancies".

On 16 August 2018, a strong evidence for the existence of Majorana bound states (or Majorana anyons) in an iron-based superconductor, which many alternative trivial explanations cannot account for, was reported by Ding's and Gao's teams at Institute of Physics, Chinese Academy of Sciences and University of Chinese Academy of Sciences, when they used scanning tunneling spectroscopy on the superconducting Dirac surface state of the iron-based superconductor. It was the first time that indications of Majorana particles were observed in a bulk of pure substance.[50] However, more recent experimental studies in iron-based superconductors show that topologically trivial Caroli–de Gennes–Matricon states [51] and Yu–Shiba–Rusinov states[52] can exhibit qualitative and quantitative features similar to those Majorana zero modes would make. In 2020 similar results were reported for a platform consisting of europium sulfide and gold films grown on vanadium.[53]

Majorana bound states in quantum error correction

One of the causes of interest in Majorana bound states is that they could be used in quantum error correcting codes.[54][55] This process is done by creating so called 'twist defects' in codes such as the toric code[56] which carry unpaired Majorana modes.[57] The Majoranas are then "braided" by being physically moved around each other in 2D sheets or networks of nanowires.[58] This braiding process forms a projective representation of the braid group.[59]

Such a realization of Majoranas would allow them to be used to store and process quantum information within a quantum computation.[60] Though the codes typically have no Hamiltonian to provide suppression of errors, fault-tolerance would be provided by the underlying quantum error correcting code.

Majorana bound states in Kitaev chains

In February 2023[61][62] a study reported the realization of a "poor man's" Majorana that is a Majorana bound state that is not topologically protected and therefore only stable for a very small range of parameters. It was obtained in Kitaev chain consisting of two quantum dots in a superconducting nanowire strongly coupled by normal tunneling and Andreev tunneling with the state arising when the rate of both processes match confirming a prediction of Kitaev.[63]

References

  1. ↑ "Quantum Computation possible with Majorana Fermions" on YouTube, uploaded 19 April 2013, retrieved 5 October 2014; and also based on the pronunciation of physicist's name.
  2. ↑ Majorana, Ettore; Maiani, Luciano (2006). "A symmetric theory of electrons and positrons". in Bassani, Giuseppe Franco. Ettore Majorana Scientific Papers. pp. 201–233. doi:10.1007/978-3-540-48095-2_10. ISBN 978-3-540-48091-4. https://archive.org/details/ettoremajoranasc00bass.  Translated from: Majorana, Ettore (1937). "Teoria simmetrica dell'elettrone e del positrone" (in it). Il Nuovo Cimento 14 (4): 171–184. doi:10.1007/bf02961314. Bibcode: 1937NCim...14..171M. 
  3. ↑ Rodejohann, Werner (2011). "Neutrino-less double beta decay and particle physics". International Journal of Modern Physics E20 (9): 1833–1930. doi:10.1142/S0218301311020186. Bibcode: 2011IJMPE..20.1833R. 
  4. ↑ Schechter, J.; Valle, J.W.F. (1982). "Neutrinoless double-β decay in SU(2) x U(1) theories". Physical Review D 25 (11): 2951–2954. doi:10.1103/PhysRevD.25.2951. Bibcode: 1982PhRvD..25.2951S. http://roderic.uv.es/bitstream/10550/47205/1/073631.pdf. 
  5. ↑ Keung, Wai-Yee; Senjanović, Goran (1983). "Majorana neutrinos and the production of the right-handed charged gauge boson". Physical Review Letters 50 (19): 1427–1430. doi:10.1103/PhysRevLett.50.1427. Bibcode: 1983PhRvL..50.1427K. 
  6. ↑ Tello, Vladimir; Nemevšek, Miha; Nesti, Fabrizio; Senjanović, Goran; Vissani, Francesco (2011). "Left-right symmetry: From LHC to neutrinoless double beta decay". Physical Review Letters 106 (15): 151801. doi:10.1103/PhysRevLett.106.151801. PMID 21568545. Bibcode: 2011PhRvL.106o1801T. 
  7. ↑ Kayser, Boris; Goldhaber, Alfred S. (1983). "CPT and CP properties of Majorana particles, and the consequences". Physical Review D 28 (9): 2341–2344. doi:10.1103/PhysRevD.28.2341. Bibcode: 1983PhRvD..28.2341K. 
  8. ↑ Radescu, E.E. (1985). "On the electromagnetic properties of Majorana fermions". Physical Review D 32 (5): 1266–1268. doi:10.1103/PhysRevD.32.1266. PMID 9956279. Bibcode: 1985PhRvD..32.1266R. 
  9. ↑ Boudjema, F.; Hamzaoui, C.; Rahal, V.; Ren, H.C. (1989). "Electromagnetic Properties of Generalized Majorana Particles". Physical Review Letters 62 (8): 852–854. doi:10.1103/PhysRevLett.62.852. PMID 10040354. Bibcode: 1989PhRvL..62..852B. 
  10. ↑ Pospelov, Maxim; ter Veldhuis, Tonnis (2000). "Direct and indirect limits on the electro-magnetic form factors of WIMPs". Physics Letters B 480 (1–2): 181–186. doi:10.1016/S0370-2693(00)00358-0. Bibcode: 2000PhLB..480..181P. 
  11. ↑ Ho, Chiu Man; Scherrer, Robert J. (2013). "Anapole Dark Matter". Physics Letters B 722 (8): 341–346. doi:10.1016/j.physletb.2013.04.039. Bibcode: 2013PhLB..722..341H. 
  12. ↑ Wilczek, Frank (2009). "Majorana returns". Nature Physics 5 (9): 614–618. doi:10.1038/nphys1380. Bibcode: 2009NatPh...5..614W. http://ctp.lns.mit.edu/Wilczek_Nature/Majorana_return434.pdf. 
  13. ↑ Nayak, Chetan; Simon, Steven H.; Stern, Ady; Freedman, Michael; Das Sarma, Sankar (2008). "Non-Abelian anyons and topological quantum computation". Reviews of Modern Physics 80 (3): 1083–1159. doi:10.1103/RevModPhys.80.1083. Bibcode: 2008RvMP...80.1083N. 
  14. ↑ Kopnin, N.B.; Salomaa, M.M. (1991). "Mutual friction in superfluid 3He: Effects of bound states in the vortex core". Physical Review B 44 (17): 9667–9677. doi:10.1103/PhysRevB.44.9667. PMID 9998953. Bibcode: 1991PhRvB..44.9667K. 
  15. ↑ Volovik, G.E. (1999). "Fermion zero modes on vortices in chiral superconductors". JETP Letters 70 (9): 609–614. doi:10.1134/1.568223. Bibcode: 1999JETPL..70..609V. 
  16. ↑ Read, N.; Green, Dmitry (2000). "Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect". Physical Review B 61 (15): 10267–10297. doi:10.1103/PhysRevB.61.10267. Bibcode: 2000PhRvB..6110267R. 
  17. ↑ Kitaev, A. Yu (2001). "Unpaired Majorana fermions in quantum wires". Physics-Uspekhi Supplement 44 (131): 131–136. doi:10.1070/1063-7869/44/10S/S29. Bibcode: 2001PhyU...44..131K. 
  18. ↑ Moore, Gregory; Read, Nicholas (August 1991). "Nonabelions in the fractional quantum Hall effect". Nuclear Physics B 360 (2–3): 362–396. doi:10.1016/0550-3213(91)90407-O. Bibcode: 1991NuPhB.360..362M. 
  19. ↑ Fu, Liang; Kane, Charles L. (2008). "Superconducting proximity effect and Majorana fermions at the surface of a topological insulatorn". Physical Review Letters 10 (9): 096407. doi:10.1103/PhysRevLett.100.096407. PMID 18352737. Bibcode: 2008PhRvL.100i6407F. 
  20. ↑ Fu, Liang; Kane, Charles L. (2009). "Josephson current and noise at a superconductor/quantum-spin-Hall-insulator/superconductor junction". Physical Review B 79 (16): 161408. doi:10.1103/PhysRevB.79.161408. Bibcode: 2009PhRvB..79p1408F. 
  21. ↑ Alicea, Jason (2012). "New directions in the pursuit of Majorana fermions in solid state systems". Reports on Progress in Physics 75 (7): 076501. doi:10.1088/0034-4885/75/7/076501. PMID 22790778. Bibcode: 2012RPPh...75g6501A. 
  22. ↑ Beenakker, C.W.J. (April 2013). "Search for Majorana fermions in superconductors". Annual Review of Condensed Matter Physics 4 (113): 113–136. doi:10.1146/annurev-conmatphys-030212-184337. Bibcode: 2013ARCMP...4..113B. 
  23. ↑ Reich, Eugenie Samuel (28 February 2012). "Quest for quirky quantum particles may have struck gold". Nature News. doi:10.1038/nature.2012.10124. 
  24. ↑ Amos, Jonathan (13 April 2012). "Majorana particle glimpsed in lab". https://www.bbc.co.uk/news/science-environment-17695944. 
  25. ↑ Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. (12 April 2012). "Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices". Science 336 (6084): 1003–1007. doi:10.1126/science.1222360. PMID 22499805. Bibcode: 2012Sci...336.1003M. 
  26. ↑ Rokhinson, L.P.; Liu, X.; Furdyna, J.K. (2012). "Observation of the fractional ac Josephson effect: the signature of Majorana particles". Nature Physics 8 (11): 795–799. doi:10.1038/nphys2429. Bibcode: 2012NatPh...8..795R. 
  27. ↑ Kwon, H.-J.; Sengupta, K.; Yakovenko, V. M. (2004). "Fractional ac Josephson effect in p- and d-wave superconductors". The European Physical Journal B 37 (3): 349–361. doi:10.1140/epjb/e2004-00066-4. Bibcode: 2004EPJB...37..349K. 
  28. ↑ Deng, M.T.; Yu, C.L.; Huang, G.Y.; Larsson, M.; Caroff, P.; Xu, H.Q. (28 November 2012). "Anomalous zero-bias conductance peak in a Nb-InSb nanowire-Nb hybrid device". Nano Letters 12 (12): 6414–6419. doi:10.1021/nl303758w. PMID 23181691. Bibcode: 2012NanoL..12.6414D. 
  29. ↑ Das, A.; Ronen, Y.; Most, Y.; Oreg, Y.; Heiblum, M.; Shtrikman, H. (11 November 2012). "Zero-bias peaks and splitting in an Al-InAs nanowire topological superconductor as a signature of Majorana fermions". Nature Physics 8 (12): 887–895. doi:10.1038/nphys2479. Bibcode: 2012NatPh...8..887D. 
  30. ↑ Churchill, H.O.H.; Fatemi, V.; Grove-Rasmussen, K.; Deng, M.T.; Caroff, P.; Xu, H.Q.; Marcus, C.M. (6 June 2013). "Superconductor-nanowire devices from tunneling to the multichannel regime: Zero-bias oscillations and magnetoconductance crossover". Physical Review B 87 (24): 241401(R). doi:10.1103/PhysRevB.87.241401. Bibcode: 2013PhRvB..87x1401C. 
  31. ↑ Deng, M.T.; Yu, C.L.; Huang, G.Y.; Larsson, Marcus; Caroff, P.; Xu, H.Q. (11 November 2014). "Parity independence of the zero-bias conductance peak in a nanowire based topological superconductor-quantum dot hybrid device". Scientific Reports 4: 7261. doi:10.1038/srep07261. PMID 25434375. Bibcode: 2014NatSR...4E7261D. 
  32. ↑ Wiedenmann, J.; Bocquillon, E.; Deacon, R.S.; Hartinger, S.; Herrmann, O.; Klapwijk, T.M. et al. (2016). "4-pi-periodic Josephson supercurrent in HgTe-based topological Josephson junctions". Nature Communications 7: 10303. doi:10.1038/ncomms10303. PMID 26792013. Bibcode: 2016NatCo...710303W. 
  33. ↑ Lutchyn, Roman M.; Sau, Jay D.; Das Sarma, S. (August 2010). "Majorana Fermions and a Topological Phase Transition in Semiconductor-Superconductor Heterostructures". Physical Review Letters 105 (7): 077001. doi:10.1103/PhysRevLett.105.077001. PMID 20868069. Bibcode: 2010PhRvL.105g7001L. 
  34. ↑ Oreg, Yuval; Refael, Gil; von Oppen, Felix (October 2010). "Helical Liquids and Majorana Bound States in Quantum Wires". Physical Review Letters 105 (17): 177002. doi:10.1103/PhysRevLett.105.177002. PMID 21231073. Bibcode: 2010PhRvL.105q7002O. 
  35. ↑ Lee, E.J.H.; Jiang, X.; Houzet, M.; Aguado, R.; Lieber, C.M.; Franceschi, S.D. (15 December 2013). "Spin-resolved Andreev levels and parity crossings in hybrid superconductor–semiconductor nanostructures". Nature Nanotechnology 9 (1): 79–84. doi:10.1038/nnano.2013.267. PMID 24336403. Bibcode: 2014NatNa...9...79L. 
  36. ↑ Deng, M.T.; Vaitiekėnas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K. et al. (2016). "Majorana bound state in a coupled quantum-dot hybrid-nanowire system". Science 354 (6319): 1557–1562. doi:10.1126/science.aaf3961. PMID 28008065. Bibcode: 2016Sci...354.1557D. 
  37. ↑ Nadj-Perge, Stevan; Drozdov, Ilya K.; Li, Jian; Chen, Hua; Jeon, Sangjun; Seo, Jungpil et al. (2 October 2014). "Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor". Science 346 (6209): 602–607. doi:10.1126/science.1259327. PMID 25278507. Bibcode: 2014Sci...346..602N. 
  38. ↑ "Majorana fermion: Physicists observe elusive particle that is its own antiparticle". Phys.org (Press release). 2 October 2014. Retrieved 3 October 2014.
  39. ↑ Feldman, Benjamin E.; Randeria, Mallika T.; Li, Jian; Jeon, Sangjun; Xie, Yonglong; Wang, Zhijun et al. (March 2017). "High-resolution studies of the Majorana atomic chain platform" (in en). Nature Physics 13 (3): 286–291. doi:10.1038/nphys3947. ISSN 1745-2473. Bibcode: 2017NatPh..13..286F. http://www.nature.com/articles/nphys3947. 
  40. ↑ Jeon, Sangjun; Xie, Yonglong; Li, Jian; Wang, Zhijun; Bernevig, B. Andrei; Yazdani, Ali (2017-11-10). "Distinguishing a Majorana zero mode using spin-resolved measurements" (in en). Science 358 (6364): 772–776. doi:10.1126/science.aan3670. ISSN 0036-8075. PMID 29025997. Bibcode: 2017Sci...358..772J. https://www.science.org/doi/10.1126/science.aan3670. 
  41. ↑ Kim, Howon; Palacio-Morales, Alexandra; Posske, Thore; Rózsa, Levente; Palotás, Krisztián; Szunyogh, László et al. (2018-05-30). "Toward tailoring Majorana bound states in artificially constructed magnetic atom chains on elemental superconductors" (in en). Science Advances 4 (5): eaar5251. doi:10.1126/sciadv.aar5251. ISSN 2375-2548. PMID 29756034. Bibcode: 2018SciA....4.5251K. 
  42. ↑ Jäck, Berthold; Xie, Yonglong; Yazdani, Ali (August 2021). "Detecting and distinguishing Majorana zero modes with the scanning tunnelling microscope" (in en). Nature Reviews Physics 3 (8): 541–554. doi:10.1038/s42254-021-00328-z. ISSN 2522-5820. Bibcode: 2021NatRP...3..541J. https://www.nature.com/articles/s42254-021-00328-z. 
  43. ↑ Banerjee, A. et al. (4 April 2016). "Proximate Kitaev quantum spin liquid behaviour in a honeycomb magnet". Nature Materials 15 (7): 733–740. doi:10.1038/nmat4604. PMID 27043779. Bibcode: 2016NatMa..15..733B. 
  44. ↑ He, Qing Lin; Pan, Lei; Stern, Alexander L.; Burks, Edward C.; Che, Xiaoyu; Yin, Gen et al. (2017-07-21). "Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure" (in en). Science 357 (6348): 294–299. doi:10.1126/science.aag2792. ISSN 0036-8075. PMID 28729508. Bibcode: 2017Sci...357..294H. 
  45. ↑ Conover, Emily (20 July 2017). "Majorana fermion detected in a quantum layer cake". https://www.sciencenews.org/article/majorana-fermion-detected-quantum-layer-cake. 
  46. ↑ Kayyalha, Morteza; Xiao, Di; Zhang, Ruoxi; Shin, Jaeho; Jiang, Jue; Wang, Fei et al. (2020-01-03). "Absence of evidence for chiral Majorana modes in quantum anomalous Hall-superconductor devices" (in en). Science 367 (6473): 64–67. doi:10.1126/science.aax6361. PMID 31896711. Bibcode: 2020Sci...367...64K. 
  47. ↑ Jelena Stajic (2020-01-03). "Looking for chiral Majoranas". Science 367 (6473): 36–38. doi:10.1126/science.2020.367.6473.twis. 
  48. ↑ "The case of the elusive Majorana: The so-called 'angel particle' is still a mystery". ScienceDaily (Press release). Penn State. 2020-01-03. A 2017 report of the discovery of a particular kind of Majorana fermion – the chiral Majorana fermion, referred to as the 'angel particle' – is likely a false alarm, according to new research.
  49. ↑ "Editorial Retraction" (in en). Science 378 (6621): 718. 
  50. ↑ Wang, Dongfei; Kong, Lingyuan; Fan, Peng; Chen, Hui; Zhu, Shiyu; Liu, Wenyao et al. (2018-08-16). "Evidence for Majorana bound states in an iron-based superconductor". Science 362 (6412): 333–335. doi:10.1126/science.aao1797. ISSN 0036-8075. PMID 30115743. Bibcode: 2018Sci...362..333W. 
  51. ↑ Chen, Mingyang (2018-03-06). "Discrete energy levels of Caroli-de Gennes-Matricon states in quantum limit in FeTe0.55Se0.45". Nature Communications 9 (970): 970. doi:10.1038/s41467-018-03404-8. PMID 29511191. Bibcode: 2018NatCo...9..970C. 
  52. ↑ Chatzopoulos, Damianos (2021-01-12). "Spatially dispersing Yu-Shiba-Rusinov states in the unconventional superconductor FeTe0.55Se0.45". Nature Communications 12 (298): 298. doi:10.1038/s41467-020-20529-x. PMID 33436594. 
  53. ↑ Manna, Sujit; Wei, Peng; Xie, Yingming; Tuen Law, Kam; Lee, Patrick; Moodera, Jagadeesh (2020-04-06). "Signature of a pair of Majorana zero modes in superconducting gold surface states". PNAS 117 (16): 8775–8782. doi:10.1073/pnas.1919753117. PMID 32253317. Bibcode: 2020PNAS..117.8775M. 
  54. ↑ Nayak, Chetan; Simon, Steven H.; Stern, Ady; Freedman, Michael; Sarma, Sankar Das (2008-03-27). "Non-Abelian anyons and topological quantum computation". Reviews of Modern Physics 80 (3): 1083–1159. doi:10.1103/RevModPhys.80.1083. Bibcode: 2008RvMP...80.1083N. 
  55. ↑ Sarma, Sankar Das; Freedman, Michael; Nayak, Chetan (2015-10-27). "Majorana zero modes and topological quantum computation" (in en). npj Quantum Information 1 (1): 15001. doi:10.1038/npjqi.2015.1. ISSN 2056-6387. Bibcode: 2015npjQI...115001S. 
  56. ↑ Bombin, H. (14 July 2010). "Topological Order with a Twist: Ising Anyons from an Abelian Model". Physical Review Letters 105 (3): 030403. doi:10.1103/PhysRevLett.105.030403. PMID 20867748. Bibcode: 2010PhRvL.105c0403B. 
  57. ↑ Zheng, Huaixiu; Dua, Arpit; Jiang, Liang (2015). "Demonstrating non-Abelian statistics of Majorana fermions using twist defects". Physical Review B 92 (24): 245139. doi:10.1103/PhysRevB.92.245139. Bibcode: 2015PhRvB..92x5139Z. 
  58. ↑ "Why Majoranas are cool: Braiding and quantum computation". https://topocondmat.org/w2_majorana/braiding.html. 
  59. ↑ Barkeshli, Maissam; Jian, Chao-Ming; Qi, Xiao-Liang (2013). "Twist defects and projective non-Abelian braiding statistics". Physical Review B 87 (4): 045130. doi:10.1103/PhysRevB.87.045130. Bibcode: 2013PhRvB..87d5130B. 
  60. ↑ Hastings, M.B.; Geller, A. (2015). "Reduced space-time and time costs using dislocation codes and arbitrary ancillas". Quantum Information and Computation 15 (11–12): 0962–0986. doi:10.26421/QIC15.11-12-6. Bibcode: 2014arXiv1408.3379H. 
  61. ↑ Dvir, Tom; Wang, Guanzhong; van Loo, Nick; Liu, Chun-Xiao; Mazur, Grzegorz P.; Bordin, Alberto; ten Haaf, Sebastiaan L. D.; Wang, Ji-Yin et al. (15 February 2023). "Realization of a minimal Kitaev chain in coupled quantum dots" (in en). Nature 614 (7948): 445–450. doi:10.1038/s41586-022-05585-1. ISSN 1476-4687. PMID 36792741. Bibcode: 2023Natur.614..445D. https://www.nature.com/articles/s41586-022-05585-1. 
  62. ↑ Wright, Katherine (2023-02-15). "Evidence Found for a Majorana "Cousin"" (in en). Physics 16: 24. doi:10.1103/Physics.16.24. Bibcode: 2023PhyOJ..16...24W. https://physics.aps.org/articles/v16/24. 
  63. ↑ Kitaev, A Yu (2001-10-01). "Unpaired Majorana fermions in quantum wires". Physics-Uspekhi 44 (10S): 131–136. doi:10.1070/1063-7869/44/10S/S29. ISSN 1468-4780. Bibcode: 2001PhyU...44..131K. https://iopscience.iop.org/article/10.1070/1063-7869/44/10S/S29. 

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Majorana_fermion&oldid=3278321"