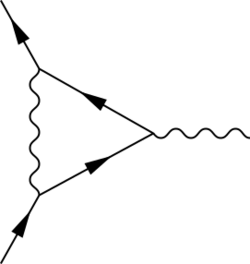
Physics:Vertex function

Short description: Effective particle coupling beyond tree level

In quantum electrodynamics, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory. In particular, it is the one particle irreducible correlation function involving the fermion [math]\displaystyle{ \psi }[/math], the antifermion [math]\displaystyle{ \bar{\psi} }[/math], and the vector potential A.

Definition

The vertex function [math]\displaystyle{ \Gamma^\mu }[/math] can be defined in terms of a functional derivative of the effective action S_eff as

[math]\displaystyle{ \Gamma^\mu = -{1\over e}{\delta^3 S_{\mathrm{eff}}\over \delta \bar{\psi} \delta \psi \delta A_\mu} }[/math]

The one-loop correction to the vertex function. This is the dominant contribution to the anomalous magnetic moment of the electron.

The dominant (and classical) contribution to [math]\displaystyle{ \Gamma^\mu }[/math] is the gamma matrix [math]\displaystyle{ \gamma^\mu }[/math], which explains the choice of the letter. The vertex function is constrained by the symmetries of quantum electrodynamics — Lorentz invariance; gauge invariance or the transversality of the photon, as expressed by the Ward identity; and invariance under parity — to take the following form:

[math]\displaystyle{ \Gamma^\mu = \gamma^\mu F_1(q^2) + \frac{i \sigma^{\mu\nu} q_{\nu}}{2 m} F_2(q^2) }[/math]

where [math]\displaystyle{ \sigma^{\mu\nu} = (i/2) [\gamma^{\mu}, \gamma^{\nu}] }[/math], [math]\displaystyle{ q_{\nu} }[/math] is the incoming four-momentum of the external photon (on the right-hand side of the figure), and F₁(q²) and F₂(q²) are form factors that depend only on the momentum transfer q². At tree level (or leading order), F₁(q²) = 1 and F₂(q²) = 0. Beyond leading order, the corrections to F₁(0) are exactly canceled by the field strength renormalization. The form factor F₂(0) corresponds to the anomalous magnetic moment a of the fermion, defined in terms of the Landé g-factor as:

[math]\displaystyle{ a = \frac{g-2}{2} = F_2(0) }[/math]

References

• Gross, F. (1993). Relativistic Quantum Mechanics and Field Theory (1st ed.). Wiley-VCH. ISBN 978-0471591139. 
• Peskin, Michael E.; Schroeder, Daniel V. (1995). An Introduction to Quantum Field Theory. Reading: Addison-Wesley. ISBN 0-201-50397-2. https://archive.org/details/introductiontoqu0000pesk. 
• Weinberg, S. (2002), Foundations, The Quantum Theory of Fields, I, Cambridge University Press, ISBN 0-521-55001-7, https://archive.org/details/quantumtheoryoff00stev