Pythagorean quadruple

Short description: Four integers where the sum of the squares of three equals the square of the fourth

All four primitive Pythagorean quadruples with only single-digit values

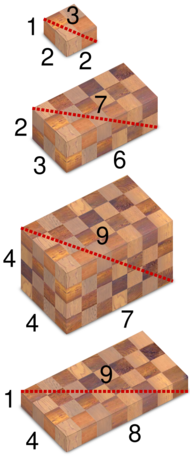
A Pythagorean quadruple is a tuple of integers a, b, c, and d, such that a² + b² + c² = d². They are solutions of a Diophantine equation and often only positive integer values are considered. However, to provide a more complete geometric interpretation, the integer values can be allowed to be negative and zero (thus allowing Pythagorean triples to be included) with the only condition being that d > 0. In this setting, a Pythagorean quadruple (a, b, c, d) defines a cuboid with integer side lengths |a|, |b|, and |c|, whose space diagonal has integer length d; with this interpretation, Pythagorean quadruples are thus also called Pythagorean boxes. In this article we will assume, unless otherwise stated, that the values of a Pythagorean quadruple are all positive integers.

Parametrization of primitive quadruples

A Pythagorean quadruple is called primitive if the greatest common divisor of its entries is 1. Every Pythagorean quadruple is an integer multiple of a primitive quadruple. The set of primitive Pythagorean quadruples for which a is odd can be generated by the formulas [math]\displaystyle{ \begin{align} a &= m^2+n^2-p^2-q^2, \\ b &= 2(mq+np), \\ c &= 2(nq-mp), \\ d &= m^2+n^2+p^2+q^2, \end{align} }[/math] where m, n, p, q are non-negative integers with greatest common divisor 1 such that m + n + p + q is odd. Thus, all primitive Pythagorean quadruples are characterized by the identity [math]\displaystyle{ (m^2 + n^2 + p^2 + q^2)^2 = (2mq + 2np)^2 + (2nq - 2mp)^2 + (m^2 + n^2 - p^2 - q^2)^2. }[/math]

Alternate parametrization

All Pythagorean quadruples (including non-primitives, and with repetition, though a, b, and c do not appear in all possible orders) can be generated from two positive integers a and b as follows:

If a and b have different parity, let p be any factor of a² + b² such that p² < a² + b². Then c = a² + b² − p²/2p and d = a² + b² + p²/2p. Note that p = d − c.

A similar method exists for generating all Pythagorean quadruples for which a and b are both even. Let l = a/2 and m = b/2 and let n be a factor of l² + m² such that n² < l² + m². Then c = l² + m² − n²/n and d = l² + m² + n²/n. This method generates all Pythagorean quadruples exactly once each when l and m run through all pairs of natural numbers and n runs through all permissible values for each pair.

No such method exists if both a and b are odd, in which case no solutions exist as can be seen by the parametrization in the previous section.

Properties

The largest number that always divides the product abcd is 12. The quadruple with the minimal product is (1, 2, 2, 3).

Similar to a Pythagorean triple which generates a distinct right triangle, a Pythagorean quadruple will generate a distinct Heronian triangle. If a, b, c, d is a Pythagorean quadruple with [math]\displaystyle{ a^2 + b^2 + c^2 = d^2 }[/math] it will generate a Heronian triangle with sides x, y, z as follows:-

[math]\displaystyle{ x = d^2 - a^2 }[/math]

[math]\displaystyle{ y = d^2 - b^2 }[/math]

[math]\displaystyle{ z = d^2 - c^2 }[/math].

It will have a semiperimeter [math]\displaystyle{ s = d^2 }[/math], an area [math]\displaystyle{ A = abcd }[/math] and an inradius [math]\displaystyle{ r = abc/d }[/math].

The exradii will be:-

[math]\displaystyle{ r_x = bcd/a }[/math]

[math]\displaystyle{ r_y = acd/b }[/math]

[math]\displaystyle{ r_z = abd/c }[/math].

The circumradius will be [math]\displaystyle{ R=(d^2 - a^2)(d^2 - b^2)(d^2 - c^2)/(4abcd) = abcd(1/a^2 + 1/b^2 + 1/c^2 -1/d^2)/4 }[/math].

The ordered sequence of areas of this class of Heronian triangles can be found at (sequence A367737 in the OEIS).

Relationship with quaternions and rational orthogonal matrices

A primitive Pythagorean quadruple (a, b, c, d) parametrized by (m, n, p, q) corresponds to the first column of the matrix representation E(α) of conjugation α(⋅)α by the Hurwitz quaternion α = m + ni + pj + qk restricted to the subspace of quaternions spanned by i, j, k, which is given by [math]\displaystyle{ E(\alpha) = \begin{pmatrix} m^2+n^2-p^2-q^2&2np-2mq &2mp+2nq \\ 2mq+2np &m^2-n^2+p^2-q^2&2pq-2mn \\ 2nq-2mp &2mn+2pq &m^2-n^2-p^2+q^2\\ \end{pmatrix}, }[/math] where the columns are pairwise orthogonal and each has norm d. Furthermore, we have that 1/dE(α) belongs to the orthogonal group [math]\displaystyle{ SO(3,\mathbb{Q}) }[/math], and, in fact, all 3 × 3 orthogonal matrices with rational coefficients arise in this manner.

Primitive Pythagorean quadruples with small norm

There are 31 primitive Pythagorean quadruples in which all entries are less than 30.

(	1	,	2	,	2	,	3	)	(	2	,	10	,	11	,	15	)	(	4	,	13	,	16	,	21	)	(	2	,	10	,	25	,	27	)
(	2	,	3	,	6	,	7	)	(	1	,	12	,	12	,	17	)	(	8	,	11	,	16	,	21	)	(	2	,	14	,	23	,	27	)
(	1	,	4	,	8	,	9	)	(	8	,	9	,	12	,	17	)	(	3	,	6	,	22	,	23	)	(	7	,	14	,	22	,	27	)
(	4	,	4	,	7	,	9	)	(	1	,	6	,	18	,	19	)	(	3	,	14	,	18	,	23	)	(	10	,	10	,	23	,	27	)
(	2	,	6	,	9	,	11	)	(	6	,	6	,	17	,	19	)	(	6	,	13	,	18	,	23	)	(	3	,	16	,	24	,	29	)
(	6	,	6	,	7	,	11	)	(	6	,	10	,	15	,	19	)	(	9	,	12	,	20	,	25	)	(	11	,	12	,	24	,	29	)
(	3	,	4	,	12	,	13	)	(	4	,	5	,	20	,	21	)	(	12	,	15	,	16	,	25	)	(	12	,	16	,	21	,	29	)
(	2	,	5	,	14	,	15	)	(	4	,	8	,	19	,	21	)	(	2	,	7	,	26	,	27	)

See also

• Beal conjecture
• Euler brick
• Euler's sum of powers conjecture
• Euler-Rodrigues formula for 3D rotations
• Fermat cubic
• Jacobi–Madden equation
• Lagrange's four-square theorem (every natural number can be represented as the sum of four integer squares)
• Legendre's three-square theorem (which natural numbers cannot be represented as the sum of three squares of integers)
• Prouhet–Tarry–Escott problem
• Quaternions and spatial rotation
• Taxicab number

External links

• Weisstein, Eric W.. "Pythagorean Quadruple". http://mathworld.wolfram.com/PythagoreanQuadruple.html. 
• Weisstein, Eric W.. "Lebesgue's Identity". http://mathworld.wolfram.com/LebesgueIdentity.html.