Ring lemma
In the geometry of circle packings in the Euclidean plane, the ring lemma gives a lower bound on the sizes of adjacent circles in a circle packing.[1]
Statement
The lemma states: Let [math]\displaystyle{ n }[/math] be any integer greater than or equal to three. Suppose that the unit circle is surrounded by a ring of [math]\displaystyle{ n }[/math] interior-disjoint circles, all tangent to it, with consecutive circles in the ring tangent to each other. Then the minimum radius of any circle in the ring is at least the unit fraction [math]\displaystyle{ \frac{1}{F_{2n-3}-1} }[/math] where [math]\displaystyle{ F_i }[/math] is the [math]\displaystyle{ i }[/math]th Fibonacci number.[1][2]
The sequence of minimum radii, from [math]\displaystyle{ n=3 }[/math], begins
Generalizations to three-dimensional space are also known.[3]
Construction
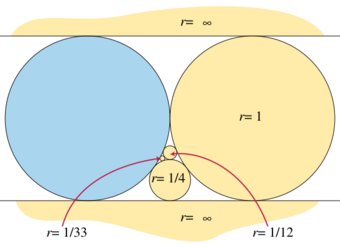
An infinite sequence of circles can be constructed, containing rings for each [math]\displaystyle{ n }[/math] that exactly meet the bound of the ring lemma, showing that it is tight. The construction allows halfplanes to be considered as degenerate circles with infinite radius, and includes additional tangencies between the circles beyond those required in the statement of the lemma. It begins by sandwiching the unit circle between two parallel halfplanes; in the geometry of circles, these are considered to be tangent to each other at the point at infinity. Each successive circle after these first two is tangent to the central unit circle and to the two most recently added circles; see the illustration for the first six circles (including the two halfplanes) constructed in this way. The first [math]\displaystyle{ n }[/math] circles of this construction form a ring, whose minimum radius can be calculated by Descartes' theorem to be the same as the radius specified in the ring lemma. This construction can be perturbed to a ring of [math]\displaystyle{ n }[/math] finite circles, without additional tangencies, whose minimum radius is arbitrarily close to this bound.[4]
History
A version of the ring lemma with a weaker bound was first proven by Burton Rodin and Dennis Sullivan as part of their proof of William Thurston's conjecture that circle packings can be used to approximate conformal maps.[5] Lowell Hansen gave a recurrence relation for the tightest possible lower bound,[6] and Dov Aharonov found a closed-form expression for the same bound.[2]
Applications
Beyond its original application to conformal mapping,[5] the circle packing theorem and the ring lemma play key roles in a proof by Keszegh, Pach, and Pálvölgyi that planar graphs of bounded degree can be drawn with bounded slope number.[7]
References
- ↑ 1.0 1.1 Stephenson, Kenneth (2005), Introduction to Circle Packing: The Theory of Discrete Analytic Functions, Cambridge University Press, ISBN 978-0-521-82356-2; see especially Lemma 8.2 (Ring Lemma), pp. 73–74, and Appendix B, The Ring Lemma, pp. 318–321.
- ↑ 2.0 2.1 Aharonov, Dov (1997), "The sharp constant in the ring lemma", Complex Variables 33 (1–4): 27–31, doi:10.1080/17476939708815009
- ↑ Vasilis, Jonatan (2011), "The ring lemma in three dimensions", Geometriae Dedicata 152: 51–62, doi:10.1007/s10711-010-9545-0
- ↑ Aharonov, D.; Stephenson, K. (1997), "Geometric sequences of discs in the Apollonian packing", Algebra i Analiz 9 (3): 104–140, https://mi.mathnet.ru/aa782
- ↑ 5.0 5.1 "The convergence of circle packings to the Riemann mapping", Journal of Differential Geometry 26 (2): 349–360, 1987, doi:10.4310/jdg/1214441375, https://projecteuclid.org/euclid.jdg/1214441375
- ↑ Hansen, Lowell J. (1988), "On the Rodin and Sullivan ring lemma", Complex Variables 10 (1): 23–30, doi:10.1080/17476938808814284
- ↑ Keszegh, Balázs (2011), "Drawing planar graphs of bounded degree with few slopes", Graph Drawing: 18th International Symposium, GD 2010, Konstanz, Germany, September 21-24, 2010, Revised Selected Papers, Lecture Notes in Computer Science, 6502, Heidelberg: Springer, pp. 293–304, doi:10.1007/978-3-642-18469-7_27
 |  |
