Slash distribution
|
Probability density function | |||
|
Cumulative distribution function | |||
| Parameters | none | ||
|---|---|---|---|
| Support | [math]\displaystyle{ x\in(-\infty,\infty) }[/math] | ||
| [math]\displaystyle{ \begin{cases} \frac{\varphi(0) - \varphi(x)}{x^2} & x \ne 0 \\ \frac{1}{2\sqrt{2\pi}} & x = 0 \\ \end{cases} }[/math] | |||
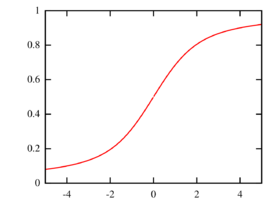
| CDF | [math]\displaystyle{ \begin{cases} \Phi(x) - \left[ \varphi(0) - \varphi(x) \right] / x & x \ne 0 \\ 1 / 2 & x = 0 \\ \end{cases} }[/math] | ||
| Mean | Does not exist | ||
| Median | 0 | ||
| Mode | 0 | ||
| Variance | Does not exist | ||
| Skewness | Does not exist | ||
| Kurtosis | Does not exist | ||
| MGF | Does not exist | ||
| CF | [math]\displaystyle{ \sqrt{2\pi}\Big(\varphi(t)+t\Phi(t)-\max\{t,0\}\Big) }[/math] | ||
In probability theory, the slash distribution is the probability distribution of a standard normal variate divided by an independent standard uniform variate.[1] In other words, if the random variable Z has a normal distribution with zero mean and unit variance, the random variable U has a uniform distribution on [0,1] and Z and U are statistically independent, then the random variable X = Z / U has a slash distribution. The slash distribution is an example of a ratio distribution. The distribution was named by William H. Rogers and John Tukey in a paper published in 1972.[2]
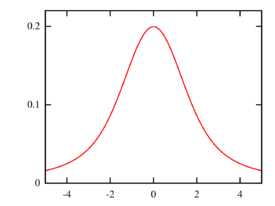
The probability density function (pdf) is
- [math]\displaystyle{ f(x) = \frac{\varphi(0) - \varphi(x)}{x^2}. }[/math]
where [math]\displaystyle{ \varphi(x) }[/math] is the probability density function of the standard normal distribution.[3] The quotient is undefined at x = 0, but the discontinuity is removable:
- [math]\displaystyle{ \lim_{x\to 0} f(x) = \frac{\varphi(0)}{2} = \frac{1}{2\sqrt{2\pi}} }[/math]
The most common use of the slash distribution is in simulation studies. It is a useful distribution in this context because it has heavier tails than a normal distribution, but it is not as pathological as the Cauchy distribution.[3]
References
- ↑ Davison, Anthony Christopher; Hinkley, D. V. (1997). Bootstrap methods and their application. Cambridge University Press. p. 484. ISBN 978-0-521-57471-6. http://www.cambridge.org/us/knowledge/isbn/item1154176/?site_locale=en_US. Retrieved 24 September 2012.
- ↑ Rogers, W. H.; Tukey, J. W. (1972). "Understanding some long-tailed symmetrical distributions". Statistica Neerlandica 26 (3): 211–226. doi:10.1111/j.1467-9574.1972.tb00191.x.
- ↑ Jump up to: 3.0 3.1 "SLAPDF". Statistical Engineering Division, National Institute of Science and Technology. http://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/slapdf.htm.
![]() This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
 |