Turn (angle)
| Turn | |
|---|---|
| Unit of | Plane angle |
| Symbol | tr, pla |
| Conversions | |
| 1 tr in ... | ... is equal to ... |
| radians | 2π rad ≈ 6.283185307... rad |
| milliradians | 2000π mrad ≈ 6283.185307... mrad |
| degrees | 360° |
| gradians | 400g |
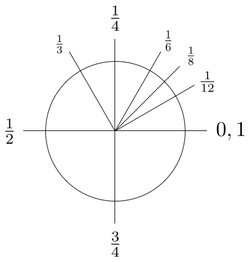
A turn is a unit of plane angle measurement equal to 2π radians, 360 degrees or 400 gradians. Subdivisions of a turn include half-turns, quarter-turns, centiturns, milliturns, etc.
One turn corresponds[1] to one cycle[2] or to one revolution,[3] although those terms may also be used, ambiguously, as shorter version of the units of frequency cycles per second (cps) and revolutions per minute (rpm), respectively.
Subdivisions
A turn can be divided in 100 centiturns or 1000 milliturns, with each milliturn corresponding to an angle of 0.36°, which can also be written as 21′ 36″.[4][5] A protractor divided in centiturns is normally called a "percentage protractor".
Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 compass points, which implicitly have an angular separation of 1/32 turn. The binary degree, also known as the binary radian (or brad), is 1/256 turn.[6] The binary degree is used in computing so that an angle can be represented to the maximum possible precision in a single byte. Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[7]
The notion of turn is commonly used for planar rotations.
History
The word turn originates via Latin and French from the Greek word τόρνος (tórnos – a lathe).
In 1697, David Gregory used π/ρ (pi over rho) to denote the perimeter of a circle (i.e., the circumference) divided by its radius.[8][9] However, earlier in 1647, William Oughtred had used δ/π (delta over pi) for the ratio of the diameter to perimeter. The first use of the symbol π on its own with its present meaning (of perimeter divided by diameter) was in 1706 by the Welsh mathematician William Jones.[10] Euler adopted the symbol with that meaning in 1737, leading to its widespread use.
The Latin word for turn is versor, which represents a rotation about an arbitrary axis in three-dimensional space. Versors form points in elliptic space and motivate the study of quaternions, an algebra developed by W. R. Hamilton in the 1840s.
Percentage protractors have existed since 1922,[11] but the terms centiturns, milliturns and microturns were introduced much later by the British astronomer Fred Hoyle in 1962.[4][5] Some measurement devices for artillery and satellite watching carry milliturn scales.[12][13]
Unit symbols
The German standard DIN 1315 (March 1974) proposed the unit symbol "pla" (from Latin: plenus angulus 'full angle') for turns.[14][15] Covered in DIN 1301-1 (de) (October 2010), the so-called Vollwinkel ('full angle') is not an SI unit. However, it is a legal unit of measurement in the EU[16][17] and Switzerland.[18]
The scientific calculators HP 39gII and HP Prime support the unit symbol "tr" for turns since 2011 and 2013, respectively. Support for "tr" was also added to newRPL for the HP 50g in 2016, and for the hp 39g+, HP 49g+, HP 39gs, and HP 40gs in 2017.[19][20] An angular mode TURN was suggested for the WP 43S as well,[21] but the calculator instead implements "MULπ" (multiples of π) as mode and unit since 2019.[22][23]
Unit conversion
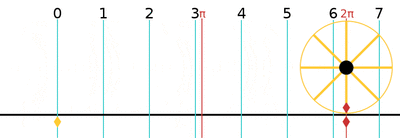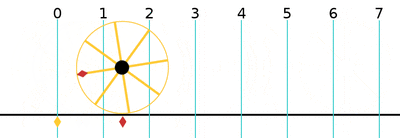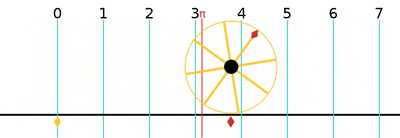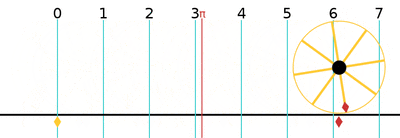
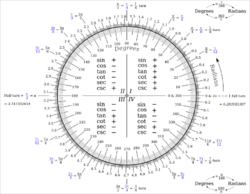
One turn is equal to 2π (≈ 6.283185307179586)[24] radians, 360 degrees, or 400 gradians.
| Turns | Radians | Degrees | Gradians | |
|---|---|---|---|---|
| 0 turn | 0 rad | 0° | 0g | |
| 1/72 turn | Template:Tau/72 rad[lower-alpha 1] | π/36 rad | 5° | 5+5/9g |
| 1/24 turn | Template:Tau/24 rad | π/12 rad | 15° | 16+2/3g |
| 1/16 turn | Template:Tau/16 rad | π/8 rad | 22.5° | 25g |
| 1/12 turn | Template:Tau/12 rad | π/6 rad | 30° | 33+1/3g |
| 1/10 turn | Template:Tau/10 rad | π/5 rad | 36° | 40g |
| 1/8 turn | Template:Tau/8 rad | π/4 rad | 45° | 50g |
| 1/2π turn | 1 rad | c. 57.3° | c. 63.7g | |
| 1/6 turn | Template:Tau/6 rad | π/3 rad | 60° | 66+2/3g |
| 1/5 turn | Template:Tau/5 rad | 2π/5 rad | 72° | 80g |
| 1/4 turn | Template:Tau/4 rad | π/2 rad | 90° | 100g |
| 1/3 turn | Template:Tau/3 rad | 2π/3 rad | 120° | 133+1/3g |
| 2/5 turn | 2Template:Tau/5 rad | 4π/5 rad | 144° | 160g |
| 1/2 turn | Template:Tau/2 rad | π rad | 180° | 200g |
| 3/4 turn | 3Template:Tau/4 rad | 3π/2 rad | 270° | 300g |
| 1 turn | Template:Tau rad | 2π rad | 360° | 400g |
- ↑ In this table, 𝜏 denotes 2π.
Proposals for a single letter to represent 2π
In 1746, Leonhard Euler first used the Greek letter pi to represent the circumference divided by the radius of a circle (i.e., π = 6.28...).[25]
In 2001, Robert Palais proposed using the number of radians in a turn as the fundamental circle constant instead of π, which amounts to the number of radians in half a turn, in order to make mathematics simpler and more intuitive. His proposal used a "π with three legs" symbol to denote the constant ().[26]
In 2008, Thomas Colignatus proposed the uppercase Greek letter theta, Θ, to represent 2π.[27] The Greek letter theta derives from the Phoenician and Hebrew letter teth, 𐤈 or ט, and it has been observed that the older version of the symbol, which means wheel, resembles a wheel with four spokes.[28] It has also been proposed to use the wheel symbol, teth, to represent the quantity 2π, and more recently a connection has been made among other ancient cultures on the existence of a wheel, sun, circle, or disk symbol—i.e. other variations of teth—as representation for 2π.[29]
In 2010, Michael Hartl proposed to use the Greek letter tau to represent the circle constant: τ = 2π. He offered two reasons. First, τ is the number of radians in one turn, which allows fractions of a turn to be expressed more directly: for instance, a 3/4 turn would be represented as 3τ/4 rad instead of 3π/2 rad. Second, τ visually resembles π, whose association with the circle constant is unavoidable.[30] Hartl's Tau Manifesto[31] gives many examples of formulas that are asserted to be clearer where τ is used instead of π,[32][33][34] such as a tighter association with the geometry of Euler's identity using eiτ = 1 instead of eiπ = −1.
Initially, neither of these proposals received widespread acceptance by the mathematical and scientific communities.[35] However, the use of τ has become more widespread,[36] for example:
- In 2012, the educational website Khan Academy began accepting answers expressed in terms of τ.[37]
- The constant τ is made available in the Google calculator, Desmos graphing calculator[38] and in several programming languages such as Python,[39][40] Raku,[41] Processing,[42] Nim,[43] Rust,[44] Java,[45] .NET,[46] and Haskell.[47]
- It has also been used in at least one mathematical research article,[48] authored by the τ-promoter Peter Harremoës.[49]
The following table shows how various identities appear if τ = 2π was used instead of π.[50][26] For a more complete list, see List of formulae involving π.
| Formula | Using π | Using τ | Notes |
|---|---|---|---|
| Angle subtended by 1/4 of a circle | Lua error: not enough memory. rad | Lua error: not enough memory. rad | Lua error: Internal error: The interpreter exited with status 1. rad = Lua error: Internal error: The interpreter exited with status 1. turn |
| Circumference C of a circle of radius r | C = 2πr | C = τr | |
| Area of a circle | A = πr2 | A = Lua error: Internal error: The interpreter exited with status 1.τr2 | The area of a sector of angle θ is A = Lua error: Internal error: The interpreter exited with status 1.θr2. |
| Area of a regular n-gon with unit circumradius | A = Lua error: Internal error: The interpreter exited with status 1. sin Lua error: Internal error: The interpreter exited with status 1. | A = Lua error: Internal error: The interpreter exited with status 1. sin Lua error: Internal error: The interpreter exited with status 1. | |
| n-ball and n-sphere volume recurrence relation | Vn(r) = Lua error: Internal error: The interpreter exited with status 1. Sn−1(r) Sn(r) = 2πr Vn−1(r) | Vn(r) = Lua error: Internal error: The interpreter exited with status 1. Sn−1(r) Sn(r) = τr Vn−1(r) | V0(r) = 1Lua error: Internal error: The interpreter exited with status 1. S0(r) = 2 |
| Cauchy's integral formula | |||
| Standard normal distribution | |||
| Stirling's approximation | |||
| Euler's identity | Lua error: Internal error: The interpreter exited with status 1. eiπ = −1 eiπ + 1 = 0 |
Lua error: Internal error: The interpreter exited with status 1.eiτ = 1 eiτ - 1 = 0 |
For any integer k, eikτ = 1 |
| nth roots of unity | |||
| Planck constant | ħ is the reduced Planck constant. | ||
| Angular frequency |
Examples of use
- As an angular unit, the turn is particularly useful in many applications, such as in connection with electromagnetic coils and rotating objects. See also Winding number.
- Pie charts illustrate proportions of a whole as fractions of a turn. Each one percent is shown as an angle of one centiturn.[11]
See also
- Ampere-turn
- Hertz (modern) or Cycle per second (older)
- Angle of rotation
- Revolutions per minute
- Repeating circle
- Spat (angular unit) – the solid angle counterpart of the turn, equivalent to 4π steradians.
- Unit interval
- Rational Trigonometry to Universal Geometry
- Modulo operation
- Twist (mathematics)
References
- ↑ Correspondence is not equivalent equality. The cycle and the revolution are not units of angle; also, this correspondence does not hold generally for cyclic phenomena.
- ↑ Fitzpatrick, R. (2021). Newtonian Dynamics: An Introduction. CRC Press. p. 116. ISBN 978-1-000-50953-3. https://books.google.com/books?id=rRpSEAAAQBAJ&pg=PA116. Retrieved 2023-04-25.
- ↑ Units & Symbols for Electrical & Electronic Engineers
- ↑ 4.0 4.1 Chandler, M. H., ed (1962). Astronomy (1 ed.). London, UK: Macdonald. OCLC 7419446. https://archive.org/details/astronom00hoyl. (320 pages)
- ↑ 5.0 5.1 "Chapter 8: Keeping Track of Time". The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Dover Books on Mathematics (corrected reprint of original ed.). Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.). 2012. p. 102. ISBN 978-0-48614497-9. https://books.google.com/books?id=CrmuSiCFyikC&pg=PA102. Retrieved 2019-08-06. (736 pages)
- ↑ "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007. http://www.oopic.com/pgchap15.htm.
- ↑ "Angles, integers, and modulo arithmetic". blogs.msdn.com. http://blogs.msdn.com/shawnhar/archive/2010/01/04/angles-integers-and-modulo-arithmetic.aspx.
- ↑ A History of Pi. Barnes & Noble Publishing. 1989.
- ↑ The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. The Mathematical Association of America. 1994. p. 165. ISBN 978-0-88385511-9. https://archive.org/details/wordsofmathemati0000schw.
- ↑ "Pi through the ages". 2001. http://www.veling.nl/anne/templars/Pi_through_the_ages.html.
- ↑ 11.0 11.1 "A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"". Journal of the American Statistical Association. Short Note 18 (137): 108–109. 1922. doi:10.1080/01621459.1922.10502455.
- ↑ "Bestimmung von Satellitenbahnen" (in de). Mitteilungen der Uraniasternwarte (Wien). 1965.
- ↑ Trackers of the Skies. History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company. 1975. https://siris-sihistory.si.edu/ipac20/ipac.jsp?&profile=all&source=~!sichronology&uri=full=3100001~!3190~!0#focus.
- ↑ (in de) Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (1 ed.). Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag. 2013-03-13. p. 421. 978-3-528-08441-7, 978-3-32283606-9. ISBN 978-3-32283606-9. https://books.google.com/books?id=63qcBgAAQBAJ&pg=PA421. Retrieved 2015-08-14.
- ↑ (in de) Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (1 ed.). Vieweg, reprint: Springer-Verlag. 2013-03-09. p. 403. doi:10.1007/978-3-322-92920-4. 978-3-322-92921-1. ISBN 978-3-32292920-4. https://books.google.com/books?id=2zecBgAAQBAJ. Retrieved 2015-08-14.
- ↑ "Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG" (in de). 1980-02-15. https://eur-lex.europa.eu/legal-content/DE/TXT/PDF/?uri=CELEX:01980L0181-20090527.
- ↑ "Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)" (in de). 2009-03-11. https://eur-lex.europa.eu/legal-content/DE/TXT/PDF/?uri=CELEX:32009L0003&from=EN.
- ↑ "Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten" (in de-ch). Einheitenverordnung. Schweizerischer Bundesrat. 1994-11-23. 941.202. http://www.admin.ch/opc/de/classified-compilation/19940345/. Retrieved 2013-01-01.
- ↑ "RE: newRPL: Handling of units". HP Museum. 2016-05-11. http://www.hpmuseum.org/forum/thread-4783-post-55836.html#pid55836.
- ↑ "Chapter 3: Units - Available Units - Angles". newRPL User Manual. 2018-10-25. https://newrpl.wiki.hpgcc3.org/doku.php?id=manual:chapter3:units#available-units. Retrieved 2019-08-07.
- ↑ "RE: WP-32S in 2016?". HP Museum. 2016-01-12. https://www.hpmuseum.org/forum/thread-5427-post-48945.html#pid48945. "[...] I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I […] found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations […] But I think it can also be useful for educational purposes. [...] Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units […]"
- ↑ WP 43S Owner's Manual (draft ed.). 2019. pp. 72, 118–119, 311. ISBN 978-1-72950098-9. https://gitlab.com/wpcalculators/wp43/-/raw/master/docs/OwnersManual.pdf. Retrieved 2019-08-05. [1] [2] (314 pages)
- ↑ WP 43S Reference Manual (draft ed.). 2019. pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. https://gitlab.com/wpcalculators/wp43/-/raw/master/docs/ReferenceManual.pdf. Retrieved 2019-08-05. [3] [4] (271 pages)
- ↑ Sequence OEIS: A019692
- ↑ Euler, L. (1746). Nova theoria lucis et colorum. Opuscula varii argumenti, p. 169–244.
- ↑ 26.0 26.1 "Pi is Wrong". The Mathematical Intelligencer (New York, USA: Springer-Verlag) 23 (3): 7–8. 2001. doi:10.1007/bf03026846. http://www.math.utah.edu/%7Epalais/pi.pdf. Retrieved 2019-08-05.
- ↑ Colignatus, Th., "Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur". 2008-04-08, Legacy:COTP.
- ↑ Mann, S., Janzen, R., Ali, M. A., Scourboutakos, P., & Guleria, N. (October 2014). Integral kinematics (time-integrals of distance, energy, etc.) and integral kinesiology. In Proceedings of the 2014 IEEE GEM, Toronto, ON, Canada (pp. 22–24)
- ↑ Mann, S., Defaz, D., Pierce, C., Lam, D., Stairs, J., Hermandez, J., ... & Mann, C. (June 2019). Keynote-Eye Itself as a Camera: Sensors, Integrity, and Trust. In The 5th ACM Workshop on Wearable Systems and Applications (pp. 1–2).
- ↑ "The Tau Manifesto". 2019-03-14. http://tauday.com/tau-manifesto.
- ↑ "The Tau Manifesto". 2010-03-14. https://hexnet.org/files/documents/tau-manifesto.pdf.
- ↑ "Michael Hartl: It's time to kill off pi". New Scientist. Interview 209 (2794): 23. 2011-01-08. doi:10.1016/S0262-4079(11)60036-5. Bibcode: 2011NewSc.209...23A.
- ↑ "On Pi Day, is 'pi' under attack?". cnn.com. CNN. 2011-03-14. http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/index.html.
- ↑ "Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful". Scientific American. 2014-06-25. http://www.scientificamerican.com/article/let-s-use-tau-it-s-easier-than-pi/.
- ↑ "Life of pi in no danger – Experts cold-shoulder campaign to replace with tau". Telegraph India. 2011-06-30. http://www.telegraphindia.com/1110630/jsp/nation/story_14178997.jsp. Retrieved 2019-08-05.
- ↑ "For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day" (in en-US). Wall Street Journal. 2020-03-13. ISSN 0099-9660. https://www.wsj.com/articles/for-math-fans-nothing-can-spoil-pi-dayexcept-maybe-tau-day-11584123031.
- ↑ "Happy Tau Day!" (in en-US). 28 June 2012. https://blog.khanacademy.org/happy-tau-day/.
- ↑ "Supported Functions". https://help.desmos.com/hc/en-us/articles/212235786-Supported-Functions.
- ↑ "PEP 628 -- Add math.tau". Python.org. 2017-02-25. https://www.python.org/dev/peps/pep-0628/.
- ↑ "math — Mathematical functions". Python 3.7.0 documentation. https://docs.python.org/3/library/math.html#math.tau.
- ↑ "Perl 6 terms". https://docs.perl6.org/language/terms.
- ↑ "TAU". Processing. https://processing.org/reference/TAU.html.
- ↑ "math". Nim. https://nim-lang.org/docs/math.html.
- ↑ "std::f64::consts::TAU - Rust". https://doc.rust-lang.org/stable/std/f64/consts/constant.TAU.html.
- ↑ "JDK-8283136: Add constant for tau to Math and StrictMath". https://bugs.openjdk.org/browse/JDK-8283136.
- ↑ John-H-K. "Add Math.Tau Pull Request #37517 · dotnet/Runtime". https://github.com/dotnet/runtime/pull/37517.
- ↑ "tau: Tau, the ratio between any circle's circumference and radius.". https://hackage.haskell.org/package/tau.
- ↑ "Bounds on tail probabilities for negative binomial distributions". Kybernetika 52 (6): 943–966. 2017. doi:10.14736/kyb-2016-6-0943.
- ↑ "Al-Kashi's constant τ". 2018-11-17. http://www.harremoes.dk/Peter/Undervis/Turnpage/Turnpage1.pdf.
- ↑ "My Conversion to Tauism". Math Horizons 19 (4): 34. April 2012. doi:10.4169/mathhorizons.19.4.34. http://www.maa.org/sites/default/files/pdf/Mathhorizons/apr12_aftermath.pdf.
Lua error: Internal error: The interpreter exited with status 1.
External links
Lua error: Internal error: The interpreter exited with status 1.