Variation of information

Short description: Measure of distance between two clusterings related to mutual information

In probability theory and information theory, the variation of information or shared information distance is a measure of the distance between two clusterings (partitions of elements). It is closely related to mutual information; indeed, it is a simple linear expression involving the mutual information. Unlike the mutual information, however, the variation of information is a true metric, in that it obeys the triangle inequality.

Information diagram illustrating the relation between information entropies, mutual information and variation of information.

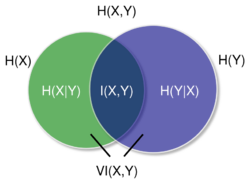
Definition

Suppose we have two partitions [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] of a set [math]\displaystyle{ A }[/math] into disjoint subsets, namely [math]\displaystyle{ X = \{X_{1}, X_{2}, \ldots, X_{k}\} }[/math] and [math]\displaystyle{ Y = \{Y_{1}, Y_{2}, \ldots, Y_{l}\} }[/math].

Let:

[math]\displaystyle{ n = \sum_{i} |X_{i}| = \sum_{j} |Y_{j}|=|A| }[/math]

[math]\displaystyle{ p_{i} = |X_{i}| / n }[/math] and [math]\displaystyle{ q_{j} = |Y_{j}| / n }[/math]

[math]\displaystyle{ r_{ij} = |X_i\cap Y_{j}| / n }[/math]

Then the variation of information between the two partitions is:

[math]\displaystyle{ \mathrm{VI}(X; Y ) = - \sum_{i,j} r_{ij} \left[\log(r_{ij}/p_i)+\log(r_{ij}/q_j) \right] }[/math].

This is equivalent to the shared information distance between the random variables i and j with respect to the uniform probability measure on [math]\displaystyle{ A }[/math] defined by [math]\displaystyle{ \mu(B):=|B|/n }[/math] for [math]\displaystyle{ B\subseteq A }[/math].

Explicit information content

We can rewrite this definition in terms that explicitly highlight the information content of this metric.

The set of all partitions of a set form a compact Lattice where the partial order induces two operations, the meet [math]\displaystyle{ \wedge }[/math] and the join [math]\displaystyle{ \vee }[/math], where the maximum [math]\displaystyle{ \overline{\mathrm{1}} }[/math] is the partition with only one block, i.e., all elements grouped together, and the minimum is [math]\displaystyle{ \overline{\mathrm{0}} }[/math], the partition consisting of all elements as singletons. The meet of two partitions [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is easy to understand as that partition formed by all pair intersections of one block of, [math]\displaystyle{ X_{i} }[/math], of [math]\displaystyle{ X }[/math] and one, [math]\displaystyle{ Y_{i} }[/math], of [math]\displaystyle{ Y }[/math]. It then follows that [math]\displaystyle{ X\wedge Y\subseteq X }[/math] and [math]\displaystyle{ X\wedge Y\subseteq Y }[/math].

Let's define the entropy of a partition [math]\displaystyle{ X }[/math] as

[math]\displaystyle{ H\left( X\right)\,=\,-\sum_i\,p_{i}\log p_{i} }[/math],

where [math]\displaystyle{ p_{i}=|X_i|/n }[/math]. Clearly, [math]\displaystyle{ H(\overline{\mathrm{1}})=0 }[/math] and [math]\displaystyle{ H(\overline{\mathrm{0}})=\log\,n }[/math]. The entropy of a partition is a monotonous function on the lattice of partitions in the sense that [math]\displaystyle{ X\subseteq Y\Rightarrow H(X) \geq H(Y) }[/math].

Then the VI distance between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] is given by

[math]\displaystyle{ \mathrm{VI}(X,Y)\,=\,2 H( X\wedge Y )\,-\,H(X)\,-\,H(Y) }[/math].

The difference [math]\displaystyle{ d(X,Y)\equiv |H\left(X\right)-H\left(Y\right)| }[/math] is a pseudo-metric as [math]\displaystyle{ d(X,Y)=0 }[/math] doesn't necessarily imply that [math]\displaystyle{ X=Y }[/math]. From the definition of [math]\displaystyle{ \overline{\mathrm{1}} }[/math], it is [math]\displaystyle{ \mathrm{VI}(X,\mathrm{1})\,=\,H\left(X\right) }[/math].

If in the Hasse diagram we draw an edge from every partition to the maximum [math]\displaystyle{ \overline{\mathrm{1}} }[/math] and assign it a weight equal to the VI distance between the given partition and [math]\displaystyle{ \overline{\mathrm{1}} }[/math], we can interpret the VI distance as basically an average of differences of edge weights to the maximum

[math]\displaystyle{ \mathrm{VI}(X,Y)\,=\,|\mathrm{VI}(X,\overline{\mathrm{1}})\,-\,\mathrm{VI}(X\wedge Y,\overline{\mathrm{1}})|\,+\,|\mathrm{VI}(Y,\overline{\mathrm{1}})\,-\,\mathrm{VI}(X\wedge Y,\overline{\mathrm{1}})| \,=\,d(X,X\wedge Y)\,+\,d(Y,X\wedge Y) }[/math].

For [math]\displaystyle{ H(X) }[/math] as defined above, it holds that the joint information of two partitions coincides with the entropy of the meet

[math]\displaystyle{ H(X,Y)\,=\,H(X\wedge Y) }[/math]

and we also have that [math]\displaystyle{ d(X,X\wedge Y)\,=\,H(X\wedge Y|X) }[/math] coincides with the conditional entropy of the meet (intersection) [math]\displaystyle{ X\wedge Y }[/math] relative to [math]\displaystyle{ X }[/math].

Identities

The variation of information satisfies

[math]\displaystyle{ \mathrm{VI}(X; Y ) = H(X) + H(Y) - 2I(X, Y) }[/math],

where [math]\displaystyle{ H(X) }[/math] is the entropy of [math]\displaystyle{ X }[/math], and [math]\displaystyle{ I(X, Y) }[/math] is mutual information between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] with respect to the uniform probability measure on [math]\displaystyle{ A }[/math]. This can be rewritten as

[math]\displaystyle{ \mathrm{VI}(X; Y ) = H(X,Y) - I(X, Y) }[/math],

where [math]\displaystyle{ H(X,Y) }[/math] is the joint entropy of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], or

[math]\displaystyle{ \mathrm{VI}(X; Y ) = H(X|Y) + H(Y|X) }[/math],

where [math]\displaystyle{ H(X|Y) }[/math] and [math]\displaystyle{ H(Y|X) }[/math] are the respective conditional entropies.

The variation of information can also be bounded, either in terms of the number of elements:

[math]\displaystyle{ \mathrm{VI}(X; Y)\leq \log(n) }[/math],

Or with respect to a maximum number of clusters, [math]\displaystyle{ K^* }[/math]:

[math]\displaystyle{ \mathrm{VI}(X ; Y) \leq 2 \log(K^*) }[/math]

Triangle inequality

To verify the triangle inequality [math]\displaystyle{ \mathrm{VI}(X; Z ) \leq \mathrm{VI}(X; Y ) + \mathrm{VI}(Y; Z) }[/math], expand using the identity [math]\displaystyle{ \mathrm{VI}(X; Y ) = H(X|Y) + H(Y|X) }[/math]. It simplifies to [math]\displaystyle{ H(X | Z) \leq H(X | Y) + H(Y | Z) }[/math]The right side equals [math]\displaystyle{ H(X, Y | Z) }[/math], which is no less than the left side. This is intuitive, as [math]\displaystyle{ X, Y | Z }[/math] contains no less randomness than [math]\displaystyle{ X|Z }[/math].

Further reading

• Arabie, P.; Boorman, S. A. (1973). "Multidimensional scaling of measures of distance between partitions". Journal of Mathematical Psychology 10 (2): 148–203. doi:10.1016/0022-2496(73)90012-6. 
• Meila, Marina (2003). "Comparing Clusterings by the Variation of Information". Learning Theory and Kernel Machines. Lecture Notes in Computer Science 2777: 173–187. doi:10.1007/978-3-540-45167-9_14. ISBN 978-3-540-40720-1. 
• Meila, M. (2007). "Comparing clusterings—an information based distance". Journal of Multivariate Analysis 98 (5): 873–895. doi:10.1016/j.jmva.2006.11.013. 
• Kingsford, Carl (2009). "Information Theory Notes". http://www.cs.umd.edu/class/spring2009/cmsc858l/InfoTheoryHints.pdf. 
• Kraskov, Alexander; Harald Stögbauer; Ralph G. Andrzejak; Peter Grassberger (2003). "Hierarchical Clustering Based on Mutual Information". arXiv:q-bio/0311039.

External links

• Partanalyzer includes a C++ implementation of VI and other metrics and indices for analyzing partitions and clusterings
• C++ implementation with MATLAB mex files