Physics:Bresler-Pister yield criterion
| Continuum mechanics |
|---|
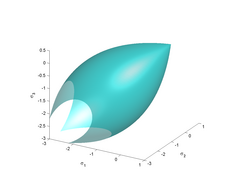
The Bresler-Pister yield criterion[1] is a function that was originally devised to predict the strength of concrete under multiaxial stress states. This yield criterion is an extension of the Drucker-Prager yield criterion and can be expressed on terms of the stress invariants as
- [math]\displaystyle{ \sqrt{J_2} = A + B~I_1 + C~I_1^2 }[/math]
where [math]\displaystyle{ I_1 }[/math] is the first invariant of the Cauchy stress, [math]\displaystyle{ J_2 }[/math] is the second invariant of the deviatoric part of the Cauchy stress, and [math]\displaystyle{ A, B, C }[/math] are material constants.
Yield criteria of this form have also been used for polypropylene [2] and polymeric foams.[3]
The parameters [math]\displaystyle{ A,B,C }[/math] have to be chosen with care for reasonably shaped yield surfaces. If [math]\displaystyle{ \sigma_c }[/math] is the yield stress in uniaxial compression, [math]\displaystyle{ \sigma_t }[/math] is the yield stress in uniaxial tension, and [math]\displaystyle{ \sigma_b }[/math] is the yield stress in biaxial compression, the parameters can be expressed as
- [math]\displaystyle{ \begin{align} B = & \left(\cfrac{\sigma_t-\sigma_c}{\sqrt{3}(\sigma_t+\sigma_c)}\right) \left(\cfrac{4\sigma_b^2 - \sigma_b(\sigma_c+\sigma_t) + \sigma_c\sigma_t}{4\sigma_b^2 + 2\sigma_b(\sigma_t-\sigma_c) - \sigma_c\sigma_t} \right) \\ C = & \left(\cfrac{1}{\sqrt{3}(\sigma_t+\sigma_c)}\right) \left(\cfrac{\sigma_b(3\sigma_t-\sigma_c) -2\sigma_c\sigma_t}{4\sigma_b^2 + 2\sigma_b(\sigma_t-\sigma_c) - \sigma_c\sigma_t} \right) \\ A = & \cfrac{\sigma_c}{\sqrt{3}} + B\sigma_c -C\sigma_c^2 \end{align} }[/math]
Derivation of expressions for parameters A, B, C The Bresler-Pister yield criterion in terms of the principal stresses [math]\displaystyle{ \sigma_1,\sigma_2,\sigma_3 }[/math] is - [math]\displaystyle{ \cfrac{1}{\sqrt{6}}\left[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2\right]^{1/2} - A - B~(\sigma_1+\sigma_2+\sigma_3) - C~(\sigma_1+\sigma_2+\sigma_3)^2 = 0~. }[/math]
If [math]\displaystyle{ \sigma_t = \sigma_1 }[/math] is the yield stress in uniaxial tension, then
- [math]\displaystyle{ \cfrac{1}{\sqrt{3}}~\sigma_t - A - B\sigma_t - C\sigma_t^2 = 0 ~. }[/math]
If [math]\displaystyle{ -\sigma_c = \sigma_1 }[/math] is the yield stress in uniaxial compression, then
- [math]\displaystyle{ \cfrac{1}{\sqrt{3}}~\sigma_c - A + B\sigma_c - C\sigma_c^2 = 0 ~. }[/math]
If [math]\displaystyle{ -\sigma_b = \sigma_1 = \sigma_2 }[/math] is the yield stress in equibiaxial compression, then
- [math]\displaystyle{ \cfrac{1}{\sqrt{3}}~\sigma_b - A + 2B\sigma_b - 4C\sigma_b^2 = 0 ~. }[/math]
Solving these three equations for [math]\displaystyle{ A,B,C }[/math] (using Maple) gives us
- [math]\displaystyle{ \begin{align} A := & \cfrac{1}{\sqrt{3}}~\cfrac{\sigma_c\sigma_t\sigma_b(\sigma_t+8\sigma_b-3\sigma_c)} {(\sigma_c+\sigma_t)(2\sigma_b-\sigma_c)(2\sigma_b+\sigma_t)} \\ B := & \cfrac{1}{\sqrt{3}}~\cfrac{(\sigma_c-\sigma_t)(\sigma_b\sigma_c+\sigma_b\sigma_t-\sigma_c\sigma_t-4\sigma_b^2)}{(\sigma_c+\sigma_t)(2\sigma_b-\sigma_c)(2\sigma_b+\sigma_t)} \\ C := & \cfrac{1}{\sqrt{3}}~\cfrac{3\sigma_b\sigma_t-\sigma_b\sigma_c-2\sigma_c\sigma_t}{(\sigma_c+\sigma_t)(2\sigma_b-\sigma_c)(2\sigma_b+\sigma_t)} \end{align} }[/math]
Alternative forms of the Bresler-Pister yield criterion
In terms of the equivalent stress ([math]\displaystyle{ \sigma_e }[/math]) and the mean stress ([math]\displaystyle{ \sigma_m }[/math]), the Bresler-Pister yield criterion can be written as
- [math]\displaystyle{ \sigma_e = a + b~\sigma_m + c~\sigma_m^2 ~;~~ \sigma_e = \sqrt{3J_2} ~,~~ \sigma_m = I_1/3 ~. }[/math]
The Etse-Willam[4] form of the Bresler-Pister yield criterion for concrete can be expressed as
- [math]\displaystyle{ \sqrt{J_2} = \cfrac{1}{\sqrt{3}}~I_1 - \cfrac{1}{2\sqrt{3}}~\left(\cfrac{\sigma_t}{\sigma_c^2-\sigma_t^2}\right)~I_1^2 }[/math]
where [math]\displaystyle{ \sigma_c }[/math] is the yield stress in uniaxial compression and [math]\displaystyle{ \sigma_t }[/math] is the yield stress in uniaxial tension.
The GAZT yield criterion[5] for plastic collapse of foams also has a form similar to the Bresler-Pister yield criterion and can be expressed as
- [math]\displaystyle{ \sqrt{J_2} = \begin{cases} \cfrac{1}{\sqrt{3}}~\sigma_t - 0.03\sqrt{3}\cfrac{\rho}{\rho_m~\sigma_t}~I_1^2 \\ -\cfrac{1}{\sqrt{3}}~\sigma_c + 0.03\sqrt{3}\cfrac{\rho}{\rho_m~\sigma_c}~I_1^2 \end{cases} }[/math]
where [math]\displaystyle{ \rho }[/math] is the density of the foam and [math]\displaystyle{ \rho_m }[/math] is the density of the matrix material.
References
- ↑ Bresler, B. and Pister, K.S., (1985), Strength of concrete under combined stresses, ACI Journal, vol. 551, no. 9, pp. 321-345.
- ↑ Pae, K. D., (1977), The macroscopic yield behavior of polymers in multiaxial stress fields, Journal of Materials Science, vol. 12, no. 6, pp. 1209-1214.
- ↑ Kim, Y. and Kang, S., (2003), Development of experimental method to characterize pressure-dependent yield criteria for polymeric foams. Polymer Testing, vol. 22, no. 2, pp. 197-202.
- ↑ Etse, G. and Willam, K., (1994), Fracture energy formulation for inelastic behavior of plain concrete, Journal of Engineering Mechanics, vol. 120, no. 9, pp. 1983-2011.
- ↑ Gibson, L. J., Ashby, M. F., Zhang, J., and Triantafillou, T. C. (1989). Failure surfaces for cellular materials under multiaxial loads. I. Modelling. International Journal of Mechanical Sciences, vol. 31, no. 9, pp. 635–663.
See also