Physics:Contact mechanics

Contact mechanics is the study of the deformation of solids that touch each other at one or more points.[1][2] A central distinction in contact mechanics is between stresses acting perpendicular to the contacting bodies' surfaces (known as normal stress) and frictional stresses acting tangentially between the surfaces (shear stress). Normal contact mechanics or frictionless contact mechanics focuses on normal stresses caused by applied normal forces and by the adhesion present on surfaces in close contact, even if they are clean and dry. Frictional contact mechanics emphasizes the effect of friction forces.
Contact mechanics is part of mechanical engineering. The physical and mathematical formulation of the subject is built upon the mechanics of materials and continuum mechanics and focuses on computations involving elastic, viscoelastic, and plastic bodies in static or dynamic contact. Contact mechanics provides necessary information for the safe and energy efficient design of technical systems and for the study of tribology, contact stiffness, electrical contact resistance and indentation hardness. Principles of contacts mechanics are implemented towards applications such as locomotive wheel-rail contact, coupling devices, braking systems, tires, bearings, combustion engines, mechanical linkages, gasket seals, metalworking, metal forming, ultrasonic welding, electrical contacts, and many others. Current challenges faced in the field may include stress analysis of contact and coupling members and the influence of lubrication and material design on friction and wear. Applications of contact mechanics further extend into the micro- and nanotechnological realm.
The original work in contact mechanics dates back to 1881 with the publication of the paper "On the contact of elastic solids"[3] ("Ueber die Berührung fester elastischer Körper") by Heinrich Hertz. Hertz was attempting to understand how the optical properties of multiple, stacked lenses might change with the force holding them together. Hertzian contact stress refers to the localized stresses that develop as two curved surfaces come in contact and deform slightly under the imposed loads. This amount of deformation is dependent on the modulus of elasticity of the material in contact. It gives the contact stress as a function of the normal contact force, the radii of curvature of both bodies and the modulus of elasticity of both bodies. Hertzian contact stress forms the foundation for the equations for load bearing capabilities and fatigue life in bearings, gears, and any other bodies where two surfaces are in contact.
History
Classical contact mechanics is most notably associated with Heinrich Hertz.[3][4] In 1882, Hertz solved the contact problem of two elastic bodies with curved surfaces. This still-relevant classical solution provides a foundation for modern problems in contact mechanics. For example, in mechanical engineering and tribology, Hertzian contact stress is a description of the stress within mating parts. The Hertzian contact stress usually refers to the stress close to the area of contact between two spheres of different radii.
It was not until nearly one hundred years later that Johnson, Kendall, and Roberts found a similar solution for the case of adhesive contact.[5] This theory was rejected by Boris Derjaguin and co-workers[6] who proposed a different theory of adhesion[7] in the 1970s. The Derjaguin model came to be known as the DMT (after Derjaguin, Muller and Toporov) model,[7] and the Johnson et al. model came to be known as the JKR (after Johnson, Kendall and Roberts) model for adhesive elastic contact. This rejection proved to be instrumental in the development of the Tabor[8] and later Maugis[6][9] parameters that quantify which contact model (of the JKR and DMT models) represent adhesive contact better for specific materials.
Further advancement in the field of contact mechanics in the mid-twentieth century may be attributed to names such as Bowden and Tabor. Bowden and Tabor were the first to emphasize the importance of surface roughness for bodies in contact.[10][11] Through investigation of the surface roughness, the true contact area between friction partners is found to be less than the apparent contact area. Such understanding also drastically changed the direction of undertakings in tribology. The works of Bowden and Tabor yielded several theories in contact mechanics of rough surfaces.
The contributions of Archard (1957)[12] must also be mentioned in discussion of pioneering works in this field. Archard concluded that, even for rough elastic surfaces, the contact area is approximately proportional to the normal force. Further important insights along these lines were provided by Greenwood and Williamson (1966),[13] Bush (1975),[14] and Persson (2002).[15] The main findings of these works were that the true contact surface in rough materials is generally proportional to the normal force, while the parameters of individual micro-contacts (i.e., pressure, size of the micro-contact) are only weakly dependent upon the load.
Classical solutions for non-adhesive elastic contact
The theory of contact between elastic bodies can be used to find contact areas and indentation depths for simple geometries. Some commonly used solutions are listed below. The theory used to compute these solutions is discussed later in the article. Solutions for multitude of other technically relevant shapes, e.g. the truncated cone, the worn sphere, rough profiles, hollow cylinders, etc. can be found in [16]
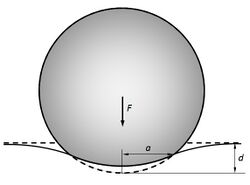
Contact between a sphere and a half-space
An elastic sphere of radius [math]\displaystyle{ R }[/math] indents an elastic half-space where total deformation is [math]\displaystyle{ d }[/math], causing a contact area of radius
- [math]\displaystyle{ a = \sqrt{Rd} }[/math]
The applied force [math]\displaystyle{ F }[/math] is related to the displacement [math]\displaystyle{ d }[/math] by [4]
- [math]\displaystyle{ F = \frac{4}{3} E^*R^\frac{1}{2}d^\frac{3}{2} }[/math]
where
- [math]\displaystyle{ \frac{1}{E^*} = \frac{1 - \nu^2_1}{E_1} + \frac{1 - \nu^2_2}{E_2} }[/math]
and [math]\displaystyle{ E_1 }[/math],[math]\displaystyle{ E_2 }[/math] are the elastic moduli and [math]\displaystyle{ \nu_1 }[/math],[math]\displaystyle{ \nu_2 }[/math] the Poisson's ratios associated with each body.
The distribution of normal pressure in the contact area as a function of distance from the center of the circle is[1]
- [math]\displaystyle{ p(r) = p_0\left(1 - \frac{r^2}{a^2}\right)^\frac{1}{2} }[/math]
where [math]\displaystyle{ p_0 }[/math] is the maximum contact pressure given by
- [math]\displaystyle{ p_0 = \frac{3F}{2\pi a^2} = \frac{1}{\pi}\left(\frac{6F{E^*}^2}{R^2}\right)^\frac{1}{3} }[/math]
The radius of the circle is related to the applied load [math]\displaystyle{ F }[/math] by the equation
- [math]\displaystyle{ a^3 = \cfrac{3FR}{4E^*} }[/math]
The total deformation [math]\displaystyle{ d }[/math] is related to the maximum contact pressure by
- [math]\displaystyle{ d = \frac{a^2}{R} = \left(\frac{9F^2}{16{E^*}^2R}\right)^\frac{1}{3} }[/math]
The maximum shear stress occurs in the interior at [math]\displaystyle{ z \approx 0.49a }[/math] for [math]\displaystyle{ \nu = 0.33 }[/math].
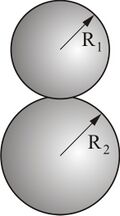
Contact between two spheres
For contact between two spheres of radii [math]\displaystyle{ R_1 }[/math] and [math]\displaystyle{ R_2 }[/math], the area of contact is a circle of radius [math]\displaystyle{ a }[/math]. The equations are the same as for a sphere in contact with a half plane except that the effective radius [math]\displaystyle{ R }[/math] is defined as [4]
- [math]\displaystyle{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} }[/math]
Contact between two crossed cylinders of equal radius
This is equivalent to contact between a sphere of radius [math]\displaystyle{ R }[/math] and a plane.
Contact between a rigid cylinder with flat end and an elastic half-space
If a rigid cylinder is pressed into an elastic half-space, it creates a pressure distribution described by[17]
- [math]\displaystyle{ p(r) = p_0\left(1 - \frac{r^2}{R^2}\right)^{-\frac{1}{2}} }[/math]
where [math]\displaystyle{ R }[/math] is the radius of the cylinder and
- [math]\displaystyle{ p_0 = \frac{1}{\pi}E^*\frac{d}{R} }[/math]
The relationship between the indentation depth and the normal force is given by
- [math]\displaystyle{ F = 2RE^*d }[/math]
Contact between a rigid conical indenter and an elastic half-space
In the case of indentation of an elastic half-space of Young's modulus [math]\displaystyle{ E }[/math] using a rigid conical indenter, the depth of the contact region [math]\displaystyle{ \epsilon }[/math] and contact radius [math]\displaystyle{ a }[/math] are related by[17]
- [math]\displaystyle{ \epsilon = a\tan(\theta) }[/math]
with [math]\displaystyle{ \theta }[/math] defined as the angle between the plane and the side surface of the cone. The total indentation depth [math]\displaystyle{ d }[/math] is given by:
- [math]\displaystyle{ d = \frac{\pi}{2}\epsilon }[/math]
The total force is
- [math]\displaystyle{ F = \frac{\pi E}{2\left(1 - \nu^2\right)} a^2 \tan(\theta) = \frac{2E}{\pi\left(1 - \nu^2\right)}\frac{d^2}{\tan(\theta)} }[/math]
The pressure distribution is given by
- [math]\displaystyle{ p\left(r\right) = \frac{Ed}{\pi a\left(1 - \nu^2\right)} \ln\left(\frac{a}{r} + \sqrt{\left(\frac{a}{r}\right)^2 - 1}\right) = \frac{Ed}{\pi a\left(1 - \nu^2\right)} \cosh^{-1}\left(\frac{a}{r}\right) }[/math]
The stress has a logarithmic singularity at the tip of the cone.
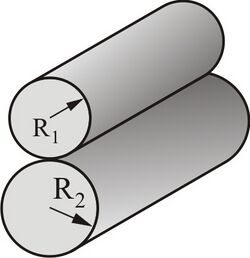
Contact between two cylinders with parallel axes
In contact between two cylinders with parallel axes, the force is linearly proportional to the length of cylinders L and to the indentation depth d:[18]
- [math]\displaystyle{ F \approx \frac{\pi}{4}E^*Ld }[/math]
The radii of curvature are entirely absent from this relationship. The contact radius is described through the usual relationship
- [math]\displaystyle{ a = \sqrt{Rd} }[/math]
with
- [math]\displaystyle{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} }[/math]
as in contact between two spheres. The maximum pressure is equal to
- [math]\displaystyle{ p_0 = \left(\frac{E^*F}{L R}\right)^\frac{1}{2} }[/math]
Bearing contact
The contact in the case of bearings is often a contact between a convex surface (male cylinder or sphere) and a concave surface (female cylinder or sphere: bore or hemispherical cup).
The Method of Dimensionality Reduction
Some contact problems can be solved with the Method of Dimensionality Reduction (MDR). In this method, the initial three-dimensional system is replaced with a contact of a body with a linear elastic or viscoelastic foundation (see fig.). The properties of one-dimensional systems coincide exactly with those of the original three-dimensional system, if the form of the bodies is modified and the elements of the foundation are defined according to the rules of the MDR.[19][20] MDR is based on the solution to axisymmetric contact problems first obtained by Ludwig Föppl (1941) and Gerhard Schubert (1942)[21]
However, for exact analytical results, it is required that the contact problem is axisymmetric and the contacts are compact.
Hertzian theory of non-adhesive elastic contact
The classical theory of contact focused primarily on non-adhesive contact where no tension force is allowed to occur within the contact area, i.e., contacting bodies can be separated without adhesion forces. Several analytical and numerical approaches have been used to solve contact problems that satisfy the no-adhesion condition. Complex forces and moments are transmitted between the bodies where they touch, so problems in contact mechanics can become quite sophisticated. In addition, the contact stresses are usually a nonlinear function of the deformation. To simplify the solution procedure, a frame of reference is usually defined in which the objects (possibly in motion relative to one another) are static. They interact through surface tractions (or pressures/stresses) at their interface.
As an example, consider two objects which meet at some surface [math]\displaystyle{ S }[/math] in the ([math]\displaystyle{ x }[/math],[math]\displaystyle{ y }[/math])-plane with the [math]\displaystyle{ z }[/math]-axis assumed normal to the surface. One of the bodies will experience a normally-directed pressure distribution [math]\displaystyle{ p_z=p(x,y)=q_z(x,y) }[/math] and in-plane surface traction distributions [math]\displaystyle{ q_x=q_x(x,y) }[/math] and [math]\displaystyle{ q_y=q_y(x,y) }[/math] over the region [math]\displaystyle{ S }[/math]. In terms of a Newtonian force balance, the forces:
- [math]\displaystyle{ P_z = \int_S p(x,y)~ \mathrm{d}A ~;~~ Q_x = \int_S q_x(x,y)~ \mathrm{d}A ~;~~ Q_y = \int_S q_y(x,y)~ \mathrm{d}A }[/math]
must be equal and opposite to the forces established in the other body. The moments corresponding to these forces:
- [math]\displaystyle{ M_x = \int_S y~q_z(x,y)~ \mathrm{d}A ~;~~ M_y = \int_S -x~q_z(x,y)~ \mathrm{d}A ~;~~ M_z = \int_S [x~q_y(x,y) - y~q_x(x,y)]~ \mathrm{d}A }[/math]
are also required to cancel between bodies so that they are kinematically immobile.
Assumptions in Hertzian theory
The following assumptions are made in determining the solutions of Hertzian contact problems:
- The strains are small and within the elastic limit.
- The surfaces are continuous and non-conforming (implying that the area of contact is much smaller than the characteristic dimensions of the contacting bodies).
- Each body can be considered an elastic half-space.
- The surfaces are frictionless.
Additional complications arise when some or all these assumptions are violated and such contact problems are usually called non-Hertzian.
Analytical solution techniques
Analytical solution methods for non-adhesive contact problem can be classified into two types based on the geometry of the area of contact.[22] A conforming contact is one in which the two bodies touch at multiple points before any deformation takes place (i.e., they just "fit together"). A non-conforming contact is one in which the shapes of the bodies are dissimilar enough that, under zero load, they only touch at a point (or possibly along a line). In the non-conforming case, the contact area is small compared to the sizes of the objects and the stresses are highly concentrated in this area. Such a contact is called concentrated, otherwise it is called diversified.
A common approach in linear elasticity is to superpose a number of solutions each of which corresponds to a point load acting over the area of contact. For example, in the case of loading of a half-plane, the Flamant solution is often used as a starting point and then generalized to various shapes of the area of contact. The force and moment balances between the two bodies in contact act as additional constraints to the solution.
Point contact on a (2D) half-plane
A starting point for solving contact problems is to understand the effect of a "point-load" applied to an isotropic, homogeneous, and linear elastic half-plane, shown in the figure to the right. The problem may be either plane stress or plane strain. This is a boundary value problem of linear elasticity subject to the traction boundary conditions:
- [math]\displaystyle{ \sigma_{xz}(x, 0) = 0 ~;~~ \sigma_z(x, z) = -P\delta(x, z) }[/math]
where [math]\displaystyle{ \delta(x, z) }[/math] is the Dirac delta function. The boundary conditions state that there are no shear stresses on the surface and a singular normal force P is applied at (0, 0). Applying these conditions to the governing equations of elasticity produces the result
- [math]\displaystyle{ \begin{align} \sigma_{xx} & = -\frac{2P}{\pi}\frac{x^2z}{\left(x^2 + z^2\right)^2} \\ \sigma_{zz} & = -\frac{2P}{\pi}\frac{z^3}{\left(x^2 + z^2\right)^2} \\ \sigma_{xz} & = -\frac{2P}{\pi}\frac{xz^2}{\left(x^2 + z^2\right)^2} \end{align} }[/math]
for some point, [math]\displaystyle{ (x, y) }[/math], in the half-plane. The circle shown in the figure indicates a surface on which the maximum shear stress is constant. From this stress field, the strain components and thus the displacements of all material points may be determined.
Line contact on a (2D) half-plane
Normal loading over a region
Suppose, rather than a point load [math]\displaystyle{ P }[/math], a distributed load [math]\displaystyle{ p(x) }[/math] is applied to the surface instead, over the range [math]\displaystyle{ a\lt x\lt b }[/math]. The principle of linear superposition can be applied to determine the resulting stress field as the solution to the integral equations:
- [math]\displaystyle{ \begin{align} \sigma_{xx} &= -\frac{2z}{\pi}\int_a^b\frac{p\left(x'\right)\left(x - x'\right)^2\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} ~;~~ \sigma_{zz} = -\frac{2z^3}{\pi}\int_a^b\frac{p\left(x'\right)\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} \\[3pt] \sigma_{xz} &= -\frac{2z^2}{\pi}\int_a^b\frac{p\left(x'\right)\left(x - x'\right)\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} \end{align} }[/math]
Shear loading over a region
The same principle applies for loading on the surface in the plane of the surface. These kinds of tractions would tend to arise as a result of friction. The solution is similar the above (for both singular loads [math]\displaystyle{ Q }[/math] and distributed loads [math]\displaystyle{ q(x) }[/math]) but altered slightly:
- [math]\displaystyle{ \begin{align} \sigma_{xx} &= -\frac{2}{\pi}\int_a^b\frac{q\left(x'\right)\left(x - x'\right)^3\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} ~;~~ \sigma_{zz} = -\frac{2z^2}{\pi}\int_a^b\frac{q\left(x'\right)\left(x - x'\right)\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} \\[3pt] \sigma_{xz} &= -\frac{2z}{\pi}\int_a^b\frac{q\left(x'\right)\left(x - x'\right)^2\, dx'}{\left[\left(x - x'\right)^2 + z^2\right]^2} \end{align} }[/math]
These results may themselves be superposed onto those given above for normal loading to deal with more complex loads.
Point contact on a (3D) half-space
Analogously to the Flamant solution for the 2D half-plane, fundamental solutions are known for the linearly elastic 3D half-space as well. These were found by Boussinesq for a concentrated normal load and by Cerruti for a tangential load. See the section on this in Linear elasticity.
Numerical solution techniques
Distinctions between conforming and non-conforming contact do not have to be made when numerical solution schemes are employed to solve contact problems. These methods do not rely on further assumptions within the solution process since they base solely on the general formulation of the underlying equations.[23][24][25][26][27] Besides the standard equations describing the deformation and motion of bodies two additional inequalities can be formulated. The first simply restricts the motion and deformation of the bodies by the assumption that no penetration can occur. Hence the gap [math]\displaystyle{ h }[/math] between two bodies can only be positive or zero
- [math]\displaystyle{ h \ge 0 }[/math]
where [math]\displaystyle{ h = 0 }[/math] denotes contact. The second assumption in contact mechanics is related to the fact, that no tension force is allowed to occur within the contact area (contacting bodies can be lifted up without adhesion forces). This leads to an inequality which the stresses have to obey at the contact interface. It is formulated for the normal stress [math]\displaystyle{ \sigma_n = \mathbf{t} \cdot \mathbf{n} }[/math].
At locations where there is contact between the surfaces the gap is zero, i.e. [math]\displaystyle{ h = 0 }[/math], and there the normal stress is different than zero, indeed, [math]\displaystyle{ \sigma_n \lt 0 }[/math]. At locations where the surfaces are not in contact the normal stress is identical to zero; [math]\displaystyle{ \sigma_n = 0 }[/math], while the gap is positive; i.e., [math]\displaystyle{ h \gt 0 }[/math]. This type of complementarity formulation can be expressed in the so-called Kuhn–Tucker form, viz.
- [math]\displaystyle{ h \ge 0\,, \quad \sigma_n \le 0\,, \quad \sigma_n\,h = 0\,. }[/math]
These conditions are valid in a general way. The mathematical formulation of the gap depends upon the kinematics of the underlying theory of the solid (e.g., linear or nonlinear solid in two- or three dimensions, beam or shell model). By restating the normal stress [math]\displaystyle{ \sigma_n }[/math] in terms of the contact pressure, [math]\displaystyle{ p }[/math]; i.e., [math]\displaystyle{ p = -\sigma_n }[/math] the Kuhn-Tucker problem can be restated as in standard complementarity form i.e. [math]\displaystyle{ h \ge 0\,,\quad p \ge 0\,,\quad p\,h = 0\,. }[/math] In the linear elastic case the gap can be formulated as [math]\displaystyle{ {h} = h_0 + {g} + u, }[/math] where [math]\displaystyle{ h_0 }[/math]is the rigid body separation, [math]\displaystyle{ g }[/math] is the geometry/topography of the contact (cylinder and roughness) and [math]\displaystyle{ u }[/math] is the elastic deformation/deflection. If the contacting bodies are approximated as linear elastic half spaces, the Boussinesq-Cerruti integral equation solution can be applied to express the deformation ([math]\displaystyle{ u }[/math]) as a function of the contact pressure ([math]\displaystyle{ p }[/math]); i.e.,[math]\displaystyle{ u = \int_\infty^\infty K(x - s)p(s)ds, }[/math] where [math]\displaystyle{ K(x - s) = \frac{2}{\pi E^*}\ln|x - s| }[/math]for line loading of an elastic half space and [math]\displaystyle{ K(x - s) = \frac{1}{\pi E^*}\frac{1}{\sqrt{\left(x_1 - s_1\right)^2 + \left(x_2 - s_2\right)^2}} }[/math] for point loading of an elastic half-space.[1]
After discretization the linear elastic contact mechanics problem can be stated in standard Linear Complementarity Problem (LCP) form.[28]
- [math]\displaystyle{ \begin{align} \mathbf{h} &= \mathbf{h}_0 + \mathbf{g} + \mathbf{Cp}, \\ \mathbf{h} \cdot \mathbf{p} &= 0,\,\,\,\mathbf{p} \geq 0,\,\,\, \mathbf{h} \geq 0,\\ \end{align} }[/math]
where [math]\displaystyle{ \mathbf{C} }[/math] is a matrix, whose elements are so called influence coefficients relating the contact pressure and the deformation. The strict LCP formulation of the CM problem presented above, allows for direct application of well-established numerical solution techniques such as Lemke's pivoting algorithm. The Lemke algorithm has the advantage that it finds the numerically exact solution within a finite number of iterations. The MATLAB implementation presented by Almqvist et al. is one example that can be employed to solve the problem numerically. In addition, an example code for an LCP solution of a 2D linear elastic contact mechanics problem has also been made public at MATLAB file exchange by Almqvist et al.
Contact between rough surfaces
When two bodies with rough surfaces are pressed against each other, the true contact area formed between the two bodies, [math]\displaystyle{ A }[/math], is much smaller than the apparent or nominal contact area [math]\displaystyle{ A_0 }[/math]. The mechanics of contacting rough surfaces are discussed in terms of normal contact mechanics and static frictional interactions.[29] Natural and engineering surfaces typically exhibit roughness features, known as asperities, across a broad range of length scales down to the molecular level, with surface structures exhibiting self affinity, also known as surface fractality. It is recognized that the self affine structure of surfaces is the origin of the linear scaling of true contact area with applied pressure.[30][31] Assuming a model of shearing welded contacts in tribological interactions, this ubiquitously observed linearity between contact area and pressure can also be considered the origin of the linearity of the relationship between static friction and applied normal force.[29]
In contact between a "random rough" surface and an elastic half-space, the true contact area is related to the normal force [math]\displaystyle{ F }[/math] by[1][31][32][33]
- [math]\displaystyle{ A=\frac{\kappa}{E^*h'}F }[/math]
with [math]\displaystyle{ h' }[/math] equal to the root mean square (also known as the quadratic mean) of the surface slope and [math]\displaystyle{ \kappa \approx2 }[/math] . The median pressure in the true contact surface
- [math]\displaystyle{ p_{\mathrm{av}} =\frac{F}{A}\approx\frac{1}{2}E^*h' }[/math]
can be reasonably estimated as half of the effective elastic modulus [math]\displaystyle{ E^* }[/math] multiplied with the root mean square of the surface slope [math]\displaystyle{ h' }[/math] .
An overview of the GW model
Greenwood and Williamson in 1966 (GW)[31] proposed a theory of elastic contact mechanics of rough surfaces which is today the foundation of many theories in tribology (friction, adhesion, thermal and electrical conductance, wear, etc.). They considered the contact between a smooth rigid plane and a nominally flat deformable rough surface covered with round tip asperities of the same radius R. Their theory assumes that the deformation of each asperity is independent of that of its neighbours and is described by the Hertz model. The heights of asperities have a random distribution. The probability that asperity height is between [math]\displaystyle{ z }[/math] and [math]\displaystyle{ z + dz }[/math] is [math]\displaystyle{ \phi(z)dz }[/math]. The authors calculated the number of contact spots n, the total contact area [math]\displaystyle{ A_r }[/math] and the total load P in general case. They gave those formulas in two forms: in the basic and using standardized variables. If one assumes that N asperities covers a rough surface, then the expected number of contacts is
- [math]\displaystyle{ n = N\int_d^\infty \phi(z) dz }[/math]
The expected total area of contact can be calculated from the formula
- [math]\displaystyle{ A_a = N\pi R \int_d^\infty (z - d) \phi(z) dz }[/math]
and the expected total force is given by
- [math]\displaystyle{ P = \frac{4}{3}N E_r \sqrt{R} \int_d^\infty (z - d)^\frac{3}{2} \phi(z) dz }[/math]
where:
- R, radius of curvature of the microasperity,
- z, height of the microasperity measured from the profile line,
- d, close the surface,
- [math]\displaystyle{ E_r = \left(\frac{1 - \nu_1^2}{E_1} + \frac{1 - \nu_2^2}{E_2}\right)^{-1} }[/math], composite Young's modulus of elasticity,
- [math]\displaystyle{ E_i }[/math], modulus of elasticity of the surface,
- [math]\displaystyle{ \nu_i }[/math], Poisson's surface coefficients.
Greenwood and Williamson introduced standardized separation [math]\displaystyle{ h = d/\sigma }[/math] and standardized height distribution [math]\displaystyle{ \phi^*(s) }[/math] whose standard deviation is equal to one. Below are presented the formulas in the standardized form.
- [math]\displaystyle{ \begin{align} F_n(h) &= \int_h^\infty (s - h)^n \phi^*(s) ds \\ n &= \eta A_n F_0(h) \\ A_a &= \pi \eta A R \sigma F_1(h) \\ P &= \frac{4}{3} \eta A E_r \sqrt{R} \sigma^\frac{3}{2} F_\frac{3}{2}(h) \end{align} }[/math]
where:
- d is the separation,
- [math]\displaystyle{ A }[/math] is the nominal contact area,
- [math]\displaystyle{ \eta }[/math] is the surface density of asperities,
- [math]\displaystyle{ E^* }[/math] is the effective Young modulus.
[math]\displaystyle{ A }[/math] and [math]\displaystyle{ P }[/math] can be determined when the [math]\displaystyle{ F_n(h) }[/math] terms are calculated for the given surfaces using the convolution of the surface roughness [math]\displaystyle{ \phi^*(s) }[/math].[34] Several studies have followed the suggested curve fits for [math]\displaystyle{ F_n(h) }[/math] assuming a Gaussian surface high distribution with curve fits presented by Arcoumanis et al.[35] and Jedynak[36] among others. It has been repeatedly observed that engineering surfaces do not demonstrate Gaussian surface height distributions e.g. Peklenik.[37] Leighton et al.[38] presented fits for crosshatched IC engine cylinder liner surfaces together with a process for determining the [math]\displaystyle{ F_n(h) }[/math] terms for any measured surfaces. Leighton et al.[38] demonstrated that Gaussian fit data is not accurate for modelling any engineered surfaces and went on to demonstrate[39] that early running of the surfaces results in a gradual transition which significantly changes the surface topography, load carrying capacity and friction.
Recently the exact approximants to [math]\displaystyle{ A_r }[/math] and [math]\displaystyle{ P }[/math] were published by Jedynak.[36] They are given by the following rational formulas, which are approximants to the integrals [math]\displaystyle{ F_n(h) }[/math]. They are calculated for the Gaussian distribution of asperities, which have been shown to be unrealistic for engineering surface but can be assumed where friction, load carrying capacity or real contact area results are not critical to the analysis.[38]
- [math]\displaystyle{ F_{n}(h) = \frac{a_0 + a_1 h + a_2 h^2 + a_3 h^3}{1 + b_1 h + b_2 h^2+b_3 h^3 + b_4 h^4 + b_5 h^5 + b_6 h^6}\exp\left(-\frac{h^2}{2}\right) }[/math]
For [math]\displaystyle{ F_1(h) }[/math] the coefficients are
- [math]\displaystyle{ \begin{align}[] [a_0, a_1, a_2, a_3] &= [0.398942280401, 0.159773702775, 0.0389687688311, 0.00364356495452] \\[] [b_1, b_2, b_3, b_4, b_5, b_6] &= \left[1.653807476138, 1.170419428529, 0.448892964428, 0.0951971709160, 0.00931642803836, -6.383774657279 \times 10^{-6}\right] \end{align} }[/math]
The maximum relative error is [math]\displaystyle{ 9.93 \times 10^{-8}% }[/math].
For [math]\displaystyle{ F_\frac{3}{2}(h) }[/math] the coefficients are
- [math]\displaystyle{ \begin{align}[] [a_0, a_1, a_2, a_3] &= [0.430019993662, 0.101979509447, 0.0229040629580, 0.000688602924] \\[] [b_1, b_2, b_3, b_4, b_5,b_6] &= [1.671117125984, 1.199586555505, 0.46936532151, 0.102632881122, 0.010686348714, 0.0000517200271] \end{align} }[/math]
The maximum relative error is [math]\displaystyle{ 1.91 \times 10^{-7}% }[/math]. The paper[36] also contains the exact expressions for [math]\displaystyle{ F_n(h) }[/math]
- [math]\displaystyle{ \begin{align} F_1(h) &= \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{1}{2}h^2\right) - \frac{1}{2} h\, \operatorname{erfc}\left(\frac{h}{\sqrt{2}}\right) \\ F_\frac{3}{2}(h) &= \frac{1}{4\sqrt{\pi}}\exp\left(-\frac{h^2}{4}\right) \sqrt{h} \left(\left(h^2 + 1\right) K_{\frac{1}{4}}\left(\frac{h^2}{4}\right) - h^2 K_{\frac{3}{4}}\left(\frac{h^2}{4}\right)\right) \end{align} }[/math]
where erfc(z) means the complementary error function and [math]\displaystyle{ K_\nu(z) }[/math] is the modified Bessel function of the second kind.
For the situation where the asperities on the two surfaces have a Gaussian height distribution and the peaks can be assumed to be spherical,[31] the average contact pressure is sufficient to cause yield when [math]\displaystyle{ p_\text{av} = 1.1\sigma_y \approx 0.39 \sigma_0 }[/math] where [math]\displaystyle{ \sigma_y }[/math] is the uniaxial yield stress and [math]\displaystyle{ \sigma_0 }[/math] is the indentation hardness.[1] Greenwood and Williamson[31] defined a dimensionless parameter [math]\displaystyle{ \Psi }[/math] called the plasticity index that could be used to determine whether contact would be elastic or plastic.
The Greenwood-Williamson model requires knowledge of two statistically dependent quantities; the standard deviation of the surface roughness and the curvature of the asperity peaks. An alternative definition of the plasticity index has been given by Mikic.[32] Yield occurs when the pressure is greater than the uniaxial yield stress. Since the yield stress is proportional to the indentation hardness [math]\displaystyle{ \sigma _0 }[/math], Mikic defined the plasticity index for elastic-plastic contact to be
- [math]\displaystyle{ \Psi = \frac{E^*h'}{\sigma _0} \gt \frac{2}{3}~. }[/math]
In this definition [math]\displaystyle{ \Psi }[/math] represents the micro-roughness in a state of complete plasticity and only one statistical quantity, the rms slope, is needed which can be calculated from surface measurements. For [math]\displaystyle{ \Psi \lt \frac{2}{3} }[/math], the surface behaves elastically during contact.
In both the Greenwood-Williamson and Mikic models the load is assumed to be proportional to the deformed area. Hence, whether the system behaves plastically or elastically is independent of the applied normal force.[1]
An overview of the GT model
The model proposed by Greenwood and Tripp (GT),[40] extended the GW model to contact between two rough surfaces. The GT model is widely used in the field of elastohydrodynamic analysis.
The most frequently cited equations given by the GT model are for the asperity contact area
- [math]\displaystyle{ A_a = \pi^2 (\eta\beta\sigma)^2 AF_2(\lambda), }[/math]
and load carried by asperities
- [math]\displaystyle{ P =\frac{8\sqrt{2}}{15}\pi (\eta\beta\sigma)^2 \sqrt{\frac{\sigma}{\beta}} E' AF_\frac{5}{2}(\lambda), }[/math]
where:
- [math]\displaystyle{ \eta\beta\sigma }[/math], roughness parameter,
- [math]\displaystyle{ A }[/math], nominal contact area,
- [math]\displaystyle{ \lambda }[/math], Stribeck oil film parameter, first defined by Stribeck \cite{gt} as [math]\displaystyle{ \lambda = h/\sigma }[/math],
- [math]\displaystyle{ E' }[/math], effective elastic modulus,
- [math]\displaystyle{ F_2, F_\frac{5}{2}(\lambda) }[/math], statistical functions introduced to match the assumed Gaussian distribution of asperities.
Leighton et al.[38] presented fits for crosshatched IC engine cylinder liner surfaces together with a process for determining the [math]\displaystyle{ F_n(h) }[/math] terms for any measured surfaces. Leighton et al.[38] demonstrated that Gaussian fit data is not accurate for modelling any engineered surfaces and went on to demonstrate[39] that early running of the surfaces results in a gradual transition which significantly changes the surface topography, load carrying capacity and friction.
The exact solutions for [math]\displaystyle{ A_a }[/math] and [math]\displaystyle{ P }[/math] are firstly presented by Jedynak.[36] They are expressed by [math]\displaystyle{ F_n }[/math] as follows. They are calculated for the Gaussian distribution of asperities, which have been shown to be unrealistic for engineering surface but can be assumed where friction, load carrying capacity or real contact area results are not critical to the analysis.[38]
- [math]\displaystyle{ \begin{align} F_2 &= \frac{1}{2} \left(h^2 + 1\right)\operatorname{erfc} \left(\frac{h}{\sqrt{2}}\right) - \frac{h}{\sqrt{2\pi}}\exp\left(-\frac{h^2}{2}\right) \\ F_\frac{5}{2} &= \frac{1}{8\sqrt{\pi}}\exp\left(-\frac{h^2}{4}\right) h^\frac{3}{2} \left(\left(2h^2 + 3\right) K_\frac{3}{4} \left(\frac{h^2}{4}\right) - \left(2h^2 + 5\right) K_\frac{1}{4}\left(\frac{h^2}{4}\right)\right) \end{align} }[/math]
where erfc(z) means the complementary error function and [math]\displaystyle{ K_\nu(z) }[/math] is the modified Bessel function of the second kind.
In paper [36] one can find comprehensive review of existing approximants to [math]\displaystyle{ F_\frac{5}{2} }[/math]. New proposals give the most accurate approximants to [math]\displaystyle{ F_\frac{5}{2} }[/math] and [math]\displaystyle{ F_2 }[/math], which are reported in the literature. They are given by the following rational formulas, which are very exact approximants to integrals [math]\displaystyle{ F_n(h) }[/math]. They are calculated for the Gaussian distribution of asperities
- [math]\displaystyle{ F_n(h) = \frac{a_0 + a_1 h + a_2 h^2 + a_3 h^3}{1 + b_1 h + b_2 h^2 + b_3 h^3 + b_4 h^4 + b_5 h^5 + b_6 h^6}\exp\left(-\frac{h^2}{2}\right) }[/math]
For [math]\displaystyle{ F_2(h) }[/math] the coefficients are
- [math]\displaystyle{ \begin{align}[] [a_0, a_1, a_2, a_3] &= [0.5, 0.182536384941, 0.039812283118, 0.003684879001] \\[] [b_1, b_2, b_3, b_4, b_5, b_6] &= [1.960841785003, 1.708677456715, 0.856592986083, 0.264996791567, 0.049257843893, 0.004640740133] \end{align} }[/math]
The maximum relative error is [math]\displaystyle{ 1.68 \times 10^{-7}% }[/math].
For [math]\displaystyle{ F_\frac{5}{2}(h) }[/math] the coefficients are
- [math]\displaystyle{ \begin{align}[] [a_0, a_1, a_2, a_3] &= [0.616634218997, 0.108855827811, 0.023453835635, 0.000449332509] \\[] [b_1, b_2, b_3, b_4, b_5, b_6] &= [1.919948267476, 1.635304362591, 0.799392556572, 0.240278859212, 0.043178653945, 0.003863334276] \end{align} }[/math]
The maximum relative error is [math]\displaystyle{ 4.98 \times 10^{-8}% }[/math].
Adhesive contact between elastic bodies
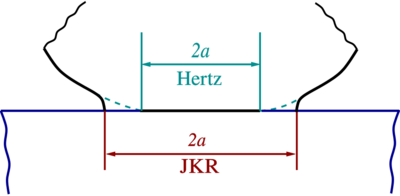
When two solid surfaces are brought into close proximity, they experience attractive van der Waals forces. Bradley's van der Waals model[41] provides a means of calculating the tensile force between two rigid spheres with perfectly smooth surfaces. The Hertzian model of contact does not consider adhesion possible. However, in the late 1960s, several contradictions were observed when the Hertz theory was compared with experiments involving contact between rubber and glass spheres.
It was observed[5] that, though Hertz theory applied at large loads, at low loads
- the area of contact was larger than that predicted by Hertz theory,
- the area of contact had a non-zero value even when the load was removed, and
- there was even strong adhesion if the contacting surfaces were clean and dry.
This indicated that adhesive forces were at work. The Johnson-Kendall-Roberts (JKR) model and the Derjaguin-Muller-Toporov (DMT) models were the first to incorporate adhesion into Hertzian contact.
Bradley model of rigid contact
It is commonly assumed that the surface force between two atomic planes at a distance [math]\displaystyle{ z }[/math] from each other can be derived from the Lennard-Jones potential. With this assumption
- [math]\displaystyle{ F(z) = \cfrac{16\gamma}{3 z_0}\left[\left(\cfrac{z}{z_0}\right)^{-9} - \left(\cfrac{z}{z_0}\right)^{-3}\right] }[/math]
where [math]\displaystyle{ F }[/math] is the force (positive in compression), [math]\displaystyle{ 2\gamma }[/math] is the total surface energy of both surfaces per unit area, and [math]\displaystyle{ z_0 }[/math] is the equilibrium separation of the two atomic planes.
The Bradley model applied the Lennard-Jones potential to find the force of adhesion between two rigid spheres. The total force between the spheres is found to be
- [math]\displaystyle{ F_a(z) = \cfrac{16\gamma\pi R}{3}\left[\cfrac{1}{4}\left(\cfrac{z}{z_0}\right)^{-8} - \left(\cfrac{z}{z_0}\right)^{-2}\right] ~;~~ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} }[/math]
where [math]\displaystyle{ R_1,R_2 }[/math] are the radii of the two spheres.
The two spheres separate completely when the pull-off force is achieved at [math]\displaystyle{ z = z_0 }[/math] at which point
- [math]\displaystyle{ F_a = F_c = -4\gamma\pi R . }[/math]
Johnson-Kendall-Roberts (JKR) model of elastic contact
To incorporate the effect of adhesion in Hertzian contact, Johnson, Kendall, and Roberts[5] formulated the JKR theory of adhesive contact using a balance between the stored elastic energy and the loss in surface energy. The JKR model considers the effect of contact pressure and adhesion only inside the area of contact. The general solution for the pressure distribution in the contact area in the JKR model is
- [math]\displaystyle{ p(r) = p_0\left(1 - \frac{r^2}{a^2}\right)^\frac{1}{2} + p_0'\left(1 - \frac{r^2}{a^2}\right)^{-\frac{1}{2}} }[/math]
Note that in the original Hertz theory, the term containing [math]\displaystyle{ p_0' }[/math] was neglected on the ground that tension could not be sustained in the contact zone. For contact between two spheres
- [math]\displaystyle{ p_0 = \frac{2aE^*}{\pi R} ;\quad p_0' = -\left(\frac{4\gamma E^*}{\pi a}\right)^\frac{1}{2} }[/math]
where [math]\displaystyle{ a\, }[/math] is the radius of the area of contact, [math]\displaystyle{ F }[/math] is the applied force, [math]\displaystyle{ 2\gamma }[/math] is the total surface energy of both surfaces per unit contact area, [math]\displaystyle{ R_i,\, E_i,\, \nu_i,~~i = 1, 2 }[/math] are the radii, Young's moduli, and Poisson's ratios of the two spheres, and
- [math]\displaystyle{ \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} ;\quad \frac{1}{E^*} = \frac{1 - \nu_1^2}{E_1} + \frac{1 - \nu_2^2}{E_2} }[/math]
The approach distance between the two spheres is given by
- [math]\displaystyle{ d = \frac{\pi a}{2E^*}\left(p_0 + 2p_0'\right) = \frac{a^2}{R} }[/math]
The Hertz equation for the area of contact between two spheres, modified to take into account the surface energy, has the form
- [math]\displaystyle{ a^3 = \frac{3R}{4E^*}\left(F + 6\gamma\pi R + \sqrt{12\gamma\pi RF + (6\gamma\pi R)^2}\right) }[/math]
When the surface energy is zero, [math]\displaystyle{ \gamma = 0 }[/math], the Hertz equation for contact between two spheres is recovered. When the applied load is zero, the contact radius is
- [math]\displaystyle{ a^3 = \frac{9R^2\gamma\pi}{E^*} }[/math]
The tensile load at which the spheres are separated (i.e., [math]\displaystyle{ a = 0 }[/math]) is predicted to be
- [math]\displaystyle{ F_\text{c} = -3\gamma\pi R\, }[/math]
This force is also called the pull-off force. Note that this force is independent of the moduli of the two spheres. However, there is another possible solution for the value of [math]\displaystyle{ a }[/math] at this load. This is the critical contact area [math]\displaystyle{ a_\text{c} }[/math], given by
- [math]\displaystyle{ a_\text{c}^3 = \frac{9R^2\gamma\pi}{4E^*} }[/math]
If we define the work of adhesion as
- [math]\displaystyle{ \Delta\gamma = \gamma_1 + \gamma_2 - \gamma_{12} }[/math]
where [math]\displaystyle{ \gamma_1, \gamma_2 }[/math] are the adhesive energies of the two surfaces and [math]\displaystyle{ \gamma_{12} }[/math] is an interaction term, we can write the JKR contact radius as
- [math]\displaystyle{ a^3 = \frac{3R}{4E^*}\left(F + 3\Delta\gamma\pi R + \sqrt{6\Delta\gamma\pi R F + (3\Delta\gamma\pi R)^2}\right) }[/math]
The tensile load at separation is
- [math]\displaystyle{ F = -\frac{3}{2}\Delta\gamma\pi R\, }[/math]
and the critical contact radius is given by
- [math]\displaystyle{ a_\text{c}^3 = \frac{9R^2\Delta\gamma\pi}{8E^*} }[/math]
The critical depth of penetration is
- [math]\displaystyle{ d_\text{c} = \frac{a_c^2}{R} = \left(R^\frac{1}{2} \frac{9\Delta\gamma\pi}{4E^*}\right)^\frac{2}{3} }[/math]
Derjaguin-Muller-Toporov (DMT) model of elastic contact
The Derjaguin-Muller-Toporov (DMT) model[7][42] is an alternative model for adhesive contact which assumes that the contact profile remains the same as in Hertzian contact but with additional attractive interactions outside the area of contact.
The radius of contact between two spheres from DMT theory is
- [math]\displaystyle{ a^3 = \cfrac{3R}{4E^*}\left(F + 4\gamma\pi R\right) }[/math]
and the pull-off force is
- [math]\displaystyle{ F_c = -4\gamma\pi R\, }[/math]
When the pull-off force is achieved the contact area becomes zero and there is no singularity in the contact stresses at the edge of the contact area.
In terms of the work of adhesion [math]\displaystyle{ \Delta\gamma }[/math]
- [math]\displaystyle{ a^3 = \cfrac{3R}{4E^*}\left(F + 2\Delta\gamma\pi R\right) }[/math]
and
- [math]\displaystyle{ F_c = -2\Delta\gamma\pi R\, }[/math]
Tabor parameter
In 1977, Tabor[43] showed that the apparent contradiction between the JKR and DMT theories could be resolved by noting that the two theories were the extreme limits of a single theory parametrized by the Tabor parameter ([math]\displaystyle{ \mu }[/math]) defined as
- [math]\displaystyle{ \mu := \frac{d_c}{z_0} \approx \left[\frac{R(\Delta\gamma)^2}{{E^*}^2 z_0^3}\right]^\frac{1}{3} }[/math]
where [math]\displaystyle{ z_0 }[/math] is the equilibrium separation between the two surfaces in contact. The JKR theory applies to large, compliant spheres for which [math]\displaystyle{ \mu }[/math] is large. The DMT theory applies for small, stiff spheres with small values of [math]\displaystyle{ \mu }[/math].
Subsequently, Derjaguin and his collaborators[44] by applying Bradley's surface force law to an elastic half space, confirmed that as the Tabor parameter increases, the pull-off force falls from the Bradley value [math]\displaystyle{ 2\pi R\Delta\gamma }[/math] to the JKR value [math]\displaystyle{ (3/2)\pi R\Delta\gamma }[/math]. More detailed calculations were later done by Greenwood[45] revealing the S-shaped load/approach curve which explains the jumping-on effect. A more efficient method of doing the calculations and additional results were given by Feng [46]
Maugis-Dugdale model of elastic contact
Further improvement to the Tabor idea was provided by Maugis[9] who represented the surface force in terms of a Dugdale cohesive zone approximation such that the work of adhesion is given by
- [math]\displaystyle{ \Delta\gamma = \sigma_0~h_0 }[/math]
where [math]\displaystyle{ \sigma_0 }[/math] is the maximum force predicted by the Lennard-Jones potential and [math]\displaystyle{ h_0 }[/math] is the maximum separation obtained by matching the areas under the Dugdale and Lennard-Jones curves (see adjacent figure). This means that the attractive force is constant for [math]\displaystyle{ z_0 \le z \le z_0 + h_0 }[/math]. There is not further penetration in compression. Perfect contact occurs in an area of radius [math]\displaystyle{ a }[/math] and adhesive forces of magnitude [math]\displaystyle{ \sigma_0 }[/math] extend to an area of radius [math]\displaystyle{ c \gt a }[/math]. In the region [math]\displaystyle{ a \lt r \lt c }[/math], the two surfaces are separated by a distance [math]\displaystyle{ h(r) }[/math] with [math]\displaystyle{ h(a) = 0 }[/math] and [math]\displaystyle{ h(c) = h_0 }[/math]. The ratio [math]\displaystyle{ m }[/math] is defined as
- [math]\displaystyle{ m := \frac{c}{a} }[/math].
In the Maugis-Dugdale theory,[47] the surface traction distribution is divided into two parts - one due to the Hertz contact pressure and the other from the Dugdale adhesive stress. Hertz contact is assumed in the region [math]\displaystyle{ -a \lt r \lt a }[/math]. The contribution to the surface traction from the Hertz pressure is given by
- [math]\displaystyle{ p^H(r) = \left(\frac{3F^H}{2\pi a^2}\right)\left(1 - \frac{r^2}{a^2}\right)^\frac{1}{2} }[/math]
where the Hertz contact force [math]\displaystyle{ F^H }[/math] is given by
- [math]\displaystyle{ F^H = \frac{4E^* a^3}{3R} }[/math]
The penetration due to elastic compression is
- [math]\displaystyle{ d^H = \frac{a^2}{R} }[/math]
The vertical displacement at [math]\displaystyle{ r = c }[/math] is
- [math]\displaystyle{ u^H(c) = \cfrac{1}{\pi R} \left[a^2\left(2 - m^2\right)\sin^{-1}\left(\frac{1}{m}\right) + a^2\sqrt{m^2 - 1}\right] }[/math]
and the separation between the two surfaces at [math]\displaystyle{ r = c }[/math] is
- [math]\displaystyle{ h^H(c) = \frac{c^2}{2R} - d^H + u^H(c) }[/math]
The surface traction distribution due to the adhesive Dugdale stress is
- [math]\displaystyle{ p^D(r) = \begin{cases} -\frac{\sigma_0}{\pi}\cos^{-1}\left[\frac{2 - m^2 - \frac{r^2}{a^2}}{m^2\left(1 - \frac{r^2}{m^2 a^2}\right)}\right] & \quad \text{for} \quad r \le a \\ -\sigma_0 & \quad \text{for} \quad a \le r \le c \end{cases} }[/math]
The total adhesive force is then given by
- [math]\displaystyle{ F^D = -2\sigma_0 m^2 a^2\left[\cos^{-1}\left(\frac{1}{m}\right) + \frac{1}{m^2}\sqrt{m^2 - 1}\right] }[/math]
The compression due to Dugdale adhesion is
- [math]\displaystyle{ d^D = -\left(\frac{2\sigma_0 a}{E^*}\right)\sqrt{m^2-1} }[/math]
and the gap at [math]\displaystyle{ r = c }[/math] is
- [math]\displaystyle{ h^D(c) = \left(\frac{4\sigma_0 a}{\pi E^*}\right)\left[\sqrt{m^2 - 1}\cos^{-1}\left(\frac{1}{m}\right) + 1 - m\right] }[/math]
The net traction on the contact area is then given by [math]\displaystyle{ p(r) = p^H(r) + p^D(r) }[/math] and the net contact force is [math]\displaystyle{ F = F^H + F^D }[/math]. When [math]\displaystyle{ h(c) = h^H(c) + h^D(c) = h_0 }[/math] the adhesive traction drops to zero.
Non-dimensionalized values of [math]\displaystyle{ a, c, F, d }[/math] are introduced at this stage that are defied as
- [math]\displaystyle{ \bar{a} = \alpha a ~;~~ \bar{c} := \alpha c ~;~~ \bar{d} := \alpha^2 Rd ~;~~ \alpha := \left(\frac{4E^*}{3\pi\Delta\gamma R^2}\right)^\frac{1}{3} ~;~~ \bar{A} := \pi c^2 ~;~~ \bar{F} = \frac{F}{\pi\Delta\gamma R} }[/math]
In addition, Maugis proposed a parameter [math]\displaystyle{ \lambda }[/math] which is equivalent to the Tabor parameter [math]\displaystyle{ \mu }[/math] . This parameter is defined as
- [math]\displaystyle{ \lambda := \sigma_0\left(\frac{9R}{2\pi\Delta\gamma{E^*}^2}\right)^\frac{1}{3}\approx 1.16\mu }[/math]
where the step cohesive stress [math]\displaystyle{ \sigma_0 }[/math] equals to the theoretical stress of the Lennard-Jones potential
- [math]\displaystyle{ \sigma_\text{th} = \frac{16\Delta\gamma}{9\sqrt{3}z_0} }[/math]
Zheng and Yu [48] suggested another value for the step cohesive stress
- [math]\displaystyle{ \sigma_0 = \exp\left(-\frac{223}{420}\right) \cdot \frac{\Delta\gamma}{z_0} \approx 0.588 \frac{\Delta\gamma}{z_0} }[/math]
to match the Lennard-Jones potential, which leads to
- [math]\displaystyle{ \lambda \approx 0.663\mu }[/math]
Then the net contact force may be expressed as
- [math]\displaystyle{ \bar{F} = \bar{a}^3 - \lambda \bar{a}^2\left[\sqrt{m^2 - 1} + m^2 \sec^{-1} m\right] }[/math]
and the elastic compression as
- [math]\displaystyle{ \bar{d} = \bar{a}^2 - \frac{4}{3}~\lambda \bar{a}\sqrt{m^2-1} }[/math]
The equation for the cohesive gap between the two bodies takes the form
- [math]\displaystyle{ \frac{\lambda \bar{a}^2}{2}\left[\left(m^2 - 2\right)\sec^{-1} m + \sqrt{m^2 - 1}\right] + \frac{4\lambda\bar{a}}{3}\left[\sqrt{m^2-1}\sec^{-1} m - m + 1\right] = 1 }[/math]
This equation can be solved to obtain values of [math]\displaystyle{ c }[/math] for various values of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ \lambda }[/math]. For large values of [math]\displaystyle{ \lambda }[/math], [math]\displaystyle{ m \rightarrow 1 }[/math] and the JKR model is obtained. For small values of [math]\displaystyle{ \lambda }[/math] the DMT model is retrieved.
Carpick-Ogletree-Salmeron (COS) model
The Maugis-Dugdale model can only be solved iteratively if the value of [math]\displaystyle{ \lambda }[/math] is not known a-priori. The Carpick-Ogletree-Salmeron approximate solution[49] simplifies the process by using the following relation to determine the contact radius [math]\displaystyle{ a }[/math]:
- [math]\displaystyle{ a = a_0(\beta) \left(\frac{\beta + \sqrt{1 - F/F_c(\beta)}}{1 + \beta}\right)^\frac{2}{3} }[/math]
where [math]\displaystyle{ a_0 }[/math] is the contact area at zero load, and [math]\displaystyle{ \beta }[/math] is a transition parameter that is related to [math]\displaystyle{ \lambda }[/math] by
- [math]\displaystyle{ \lambda \approx -0.924 \ln(1 - 1.02\beta) }[/math]
The case [math]\displaystyle{ \beta = 1 }[/math] corresponds exactly to JKR theory while [math]\displaystyle{ \beta = 0 }[/math] corresponds to DMT theory. For intermediate cases [math]\displaystyle{ 0 \lt \beta \lt 1 }[/math] the COS model corresponds closely to the Maugis-Dugdale solution for [math]\displaystyle{ 0.1 \lt \lambda \lt 5 }[/math].
Influence of contact shape
Even in the presence of perfectly smooth surfaces, geometry can come into play in form of the macroscopic shape of the contacting region. When a rigid punch with flat but oddly shaped face is carefully pulled off its soft counterpart, its detachment occurs not instantaneously but detachment fronts start at pointed corners and travel inwards, until the final configuration is reached which for macroscopically isotropic shapes is almost circular. The main parameter determining the adhesive strength of flat contacts occurs to be the maximum linear size of the contact.[50] The process of detachment can as observed experimentally can be seen in the film.[51]
See also
- Adhesive
- Adhesive bonding
- Adhesion railway
- Adhesive surface forces
- Bearing capacity
- Collision
- Contact dynamics
- Contact resistance (ECR)
- Dispersive adhesion
- Electrostatic generator
- Energetically modified cement
- Frictional contact mechanics
- Friction drive
- Galling
- Goniometer
- Non-smooth mechanics
- Plastic wrap
- Rolling (metalworking)
- Shock (mechanics)
- Signorini problem
- Surface tension
- Tribology
- Unilateral contact
- Wetting
References
See Also: Contact Mechanics for Soft Hemi-Elliptical Fingertip
- ↑ Jump up to: 1.0 1.1 1.2 1.3 1.4 1.5 Johnson, K.L. (1985). Contact Mechanics. Cambridge University Press. ISBN 978-0-521-25576-9.
- ↑ Popov, V.L. (2010). Contact Mechanics and Friction: Physical Principles and Applications. Springer Berlin Heidelberg. p. 362. ISBN 978-3-642-10803-7.
- ↑ Jump up to: 3.0 3.1 H. Hertz, 1881, Über die berührung fester elastischer Körper, Journal für die reine und angewandte Mathematik 92, pp.156-171. (For English version, see: Hertz, H., 1896. On the contact of elastic solids, In: Miscellaneous Papers, Chapter V, pp.146-162. by Hertz, H. and Lenard P., translated by Jones, D. E. and Schott G.A., London: Macmillan.
- ↑ Jump up to: 4.0 4.1 4.2 Hertz, H. R., 1882, Über die Berührung fester elastischer Körper und Über die Härte, Verhandlungen des Vereins zur Beförderung des Gewerbefleisscs, Berlin: Verein zur Beförderung des Gewerbefleisses, pp.449-463 (For English version, see: Hertz, H., 1896. On the contact of rigid elastic solids and on hardness, In: Miscellaneous Papers, Chapter VI, pp.163-183. by Hertz, H. and Lenard P., translated by Jones, D. E. and Schott G.A., London: Macmillan.
- ↑ Jump up to: 5.0 5.1 5.2 Johnson, K. L.; Kendall, K.; Roberts, A. D. (1971-09-08). "Surface energy and the contact of elastic solids". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences (The Royal Society) 324 (1558): 301–313. doi:10.1098/rspa.1971.0141. ISSN 0080-4630. Bibcode: 1971RSPSA.324..301J.
- ↑ Jump up to: 6.0 6.1 Maugis, D. (2000-02-03). Contact, Adhesion and Rupture of Elastic Solids. Springer Science & Business Media. ISBN 3-540-66113-1.
- ↑ Jump up to: 7.0 7.1 7.2 Derjaguin, B.V; Muller, V.M; Toporov, Yu.P (1975). "Effect of contact deformations on the adhesion of particles". Journal of Colloid and Interface Science (Elsevier BV) 53 (2): 314–326. doi:10.1016/0021-9797(75)90018-1. ISSN 0021-9797. Bibcode: 1975JCIS...53..314D.
- ↑ Tabor, D (1970-01-01). "The hardness of solids". Reviews of Physics in Technology (IOP Publishing) 1 (3): 145–179. doi:10.1088/0034-6683/1/3/i01. ISSN 0034-6683.
- ↑ Jump up to: 9.0 9.1 Maugis, Daniel (1992). "Adhesion of spheres: The JKR-DMT transition using a dugdale model". Journal of Colloid and Interface Science (Elsevier BV) 150 (1): 243–269. doi:10.1016/0021-9797(92)90285-t. ISSN 0021-9797. Bibcode: 1992JCIS..150..243M.
- ↑ "The area of contact between stationary and moving surfaces". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 169 (938): 391–413. 1939-02-07. doi:10.1098/rspa.1939.0005. ISSN 0080-4630.
- ↑ Bowden, F.P.; Tabor, D. (2001). The Friction and Lubrication of Solids. International series of monographs on physics. 1. Clarendon Press. ISBN 978-0-19-850777-2. https://books.google.com/books?id=OQ7FCKNixK0C.
- ↑ Archard, J. F. (1957-12-24). "Elastic deformation and the laws of friction". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 243 (1233): 190–205. doi:10.1098/rspa.1957.0214. ISSN 0080-4630. Bibcode: 1957RSPSA.243..190A.
- ↑ Greenwood, J. A.; Williamson, J. B. P. (1966-12-06). "Contact of nominally flat surfaces". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 295 (1442): 300–319. doi:10.1098/rspa.1966.0242. ISSN 0080-4630. Bibcode: 1966RSPSA.295..300G.
- ↑ Bush, A.W.; Gibson, R.D.; Thomas, T.R. (1975). "The elastic contact of a rough surface". Wear (Elsevier BV) 35 (1): 87–111. doi:10.1016/0043-1648(75)90145-3. ISSN 0043-1648.
- ↑ Persson, B. N. J.; Bucher, F.; Chiaia, B. (2002-04-29). "Elastic contact between randomly rough surfaces: Comparison of theory with numerical results". Physical Review B (American Physical Society (APS)) 65 (18): 184106. doi:10.1103/physrevb.65.184106. ISSN 0163-1829. Bibcode: 2002PhRvB..65r4106P.
- ↑ Popov, Valentin L.; Heß, Markus; Willert, Emanuel (2019) (in en). Handbook of Contact Mechanics: Exact Solutions of Axisymmetric Contact Problems. Berlin Heidelberg: Springer-Verlag. ISBN 9783662587089. https://www.springer.com/us/book/9783662587089.
- ↑ Jump up to: 17.0 17.1 Sneddon, Ian N. (1965). "The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile". International Journal of Engineering Science (Elsevier BV) 3 (1): 47–57. doi:10.1016/0020-7225(65)90019-4. ISSN 0020-7225.
- ↑ Popov, Valentin L. (2010-03-10). Contact Mechanics and Friction. Springer Science & Business Media. ISBN 978-3-642-10803-7.
- ↑ Popov, Valentin L. (2013). "Method of reduction of dimensionality in contact and friction mechanics: A linkage between micro and macro scales". Friction (Springer Science and Business Media LLC) 1 (1): 41–62. doi:10.1007/s40544-013-0005-3. ISSN 2223-7690.
- ↑ Popov, Valentin L.; Heß, Markus (2013-10-01) (in de). Methode der Dimensionsreduktion in Kontaktmechanik und Reibung. Springer-Verlag. ISBN 978-3-642-32673-8.
- ↑ Popova, Elena; Popov, Valentin L. (2020). "Ludwig Föppl and Gerhard Schubert: Unknown classics of contact mechanics" (in en). ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik 100 (9): e202000203. doi:10.1002/zamm.202000203. Bibcode: 2020ZaMM..100E0203P.
- ↑ Shigley, Joseph Edward; Mischke, Charles R. (1989). "Ch. 2". Mechanical Engineering Design (5th ed.). McGraw-Hill Science, Engineering & Mathematics. ISBN 0-07-056899-5.
- ↑ Kalker, J.J. (1990). Three-Dimensional Elastic Bodies in Rolling Contact. Solid Mechanics and Its Applications. Springer Netherlands. ISBN 978-0-7923-0712-9. https://books.google.com/books?id=DBLiT7I4qEQC.
- ↑ Wriggers, P. (2006). Computational Contact Mechanics (2nd ed.). Springer Berlin Heidelberg. ISBN 978-3-540-32609-0. https://books.google.com/books?id=oBMBy4eMYsQC.
- ↑ Laursen, T.A. (2003). Computational Contact and Impact Mechanics: Fundamentals of Modeling Interfacial Phenomena in Nonlinear Finite Element Analysis. Engineering online library. Springer Berlin Heidelberg. ISBN 978-3-540-42906-7. https://books.google.com/books?id=umzsErNuyFgC.
- ↑ Acary, V.; Brogliato, B. (2008). Numerical Methods for Nonsmooth Dynamical Systems: Applications in Mechanics and Electronics. Lecture Notes in Applied and Computational Mechanics. Springer Berlin Heidelberg. ISBN 978-3-540-75392-6. https://books.google.com/books?id=wP3-U0A5E7EC.
- ↑ Popov, Valentin L. (2009) (in de). Kontaktmechanik und Reibung. Springer Science & Business Media. ISBN 978-3-540-88836-9.
- ↑ Cottle, R.; Pang, J.; Stone, R. (2009-01-01). The Linear Complementarity Problem. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics. doi:10.1137/1.9780898719000. ISBN 9780898716863.
- ↑ Jump up to: 29.0 29.1 Hanaor, D.; Gan, Y.; Einav, I. (2016). "Static friction at fractal interfaces". Tribology International 93: 229–238. doi:10.1016/j.triboint.2015.09.016. https://www.researchgate.net/publication/283675011.
- ↑ Zhai, Chongpu; Hanaor, Dorian; Gan, Yixiang (2017). "Contact stiffness of multiscale surfaces by truncation analysis". International Journal of Mechanical Sciences (Elsevier BV) 131-132: 305–316. doi:10.1016/j.ijmecsci.2017.07.018. ISSN 0020-7403.
- ↑ Jump up to: 31.0 31.1 31.2 31.3 31.4 Greenwood, J. A.; Williamson, J. B. P. (1966-12-06). "Contact of nominally flat surfaces". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 295 (1442): 300–319. doi:10.1098/rspa.1966.0242. ISSN 0080-4630. Bibcode: 1966RSPSA.295..300G.
- ↑ Jump up to: 32.0 32.1 Mikić, B.B. (1974). "Thermal contact conductance; theoretical considerations". International Journal of Heat and Mass Transfer (Elsevier BV) 17 (2): 205–214. doi:10.1016/0017-9310(74)90082-9. ISSN 0017-9310.
- ↑ Hyun, Sangil; Robbins, Mark O. (2007). "Elastic contact between rough surfaces: Effect of roughness at large and small wavelengths". Tribology International (Elsevier BV) 40 (10–12): 1413–1422. doi:10.1016/j.triboint.2007.02.003. ISSN 0301-679X.
- ↑ Leighton (2016). "Surface-specific flow factors for prediction of friction of cross-hatched surfaces" (in en). Surface Topography: Metrology and Properties 4 (2): 025002. doi:10.1088/2051-672x/4/2/025002. Bibcode: 2016SuTMP...4b5002L. https://repository.lboro.ac.uk/articles/journal_contribution/Surface-specific_flow_factors_for_prediction_of_friction_of_crosshatched_surfaces/9566948/1/files/17199281.pdf.
- ↑ Arcoumanis, C.; Ostovar, P.; Mortier, R. (1997-10-01). "SAE Technical Paper Series" (in English). 1. Warrendale, PA. doi:10.4271/972924.
- ↑ Jump up to: 36.0 36.1 36.2 36.3 36.4 Jedynak, Radosław (2019). "Exact and approximate solutions of the infinite integrals of the asperity height distribution for the Greenwood-Williamson and the Greenwood-Tripp asperity contact models". Tribology International (Elsevier BV) 130: 206–215. doi:10.1016/j.triboint.2018.09.009. ISSN 0301-679X.
- ↑ Peklenik, J. (September 1967). "Paper 24: New Developments in Surface Characterization and Measurements by Means of Random Process Analysis". Proceedings of the Institution of Mechanical Engineers, Conference Proceedings 182 (11): 108–126. doi:10.1243/pime_conf_1967_182_309_02. ISSN 0367-8849. https://journals.sagepub.com/doi/10.1243/PIME_CONF_1967_182_309_02.
- ↑ Jump up to: 38.0 38.1 38.2 38.3 38.4 38.5 Leighton, M.; Morris, N.; Rahmani, R.; Rahnejat, H. (2017-01-01). "Surface specific asperity model for prediction of friction in boundary and mixed regimes of lubrication" (in en). Meccanica 52 (1): 21–33. doi:10.1007/s11012-016-0397-z. ISSN 1572-9648. https://repository.lboro.ac.uk/articles/journal_contribution/Surface_specific_asperity_model_for_prediction_of_friction_in_boundary_and_mixed_regimes_of_lubrication/9577130/1/files/17211284.pdf.
- ↑ Jump up to: 39.0 39.1 Leighton, M; Morris, N; Gore, M; Rahmani, R; Rahnejat, H; King, PD (2016-08-05). "Boundary interactions of rough non-Gaussian surfaces". Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology 230 (11): 1359–1370. doi:10.1177/1350650116656967. ISSN 1350-6501.
- ↑ Greenwood, J. A.; Tripp, J. H. (1970). "The Contact of Two Nominally Flat Rough Surfaces". Proceedings of the Institution of Mechanical Engineers (SAGE Publications) 185 (1): 625–633. doi:10.1243/pime_proc_1970_185_069_02. ISSN 0020-3483.
- ↑ Bradley, R.S. (1932). "LXXIX.The cohesive force between solid surfaces and the surface energy of solids". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Informa UK Limited) 13 (86): 853–862. doi:10.1080/14786449209461990. ISSN 1941-5982.
- ↑ Muller, V.M.; Derjaguin, B.V.; Toporov, Yu.P. (1983). "On two methods of calculation of the force of sticking of an elastic sphere to a rigid plane". Colloids and Surfaces (Elsevier BV) 7 (3): 251–259. doi:10.1016/0166-6622(83)80051-1. ISSN 0166-6622.
- ↑ TABOR, D. (1977). "Surface Forces and Surface Interactions". Plenary and Invited Lectures. Elsevier. p. 3–14. doi:10.1016/b978-0-12-404501-9.50009-2. ISBN 9780124045019.
- ↑ Muller, V.M; Yushchenko, V.S; Derjaguin, B.V (1980). "On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane". Journal of Colloid and Interface Science (Elsevier BV) 77 (1): 91–101. doi:10.1016/0021-9797(80)90419-1. ISSN 0021-9797. Bibcode: 1980JCIS...77...91M.
- ↑ Greenwood, J. A. (1997-06-08). "Adhesion of elastic spheres". Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences (The Royal Society) 453 (1961): 1277–1297. doi:10.1098/rspa.1997.0070. ISSN 1364-5021. Bibcode: 1997RSPSA.453.1277G.
- ↑ Feng, James Q. (2000). "Contact behavior of spherical elastic particles: a computational study of particle adhesion and deformations". Colloids and Surfaces A: Physicochemical and Engineering Aspects (Elsevier BV) 172 (1–3): 175–198. doi:10.1016/s0927-7757(00)00580-x. ISSN 0927-7757.
- ↑ Johnson, K.L.; Greenwood, J.A. (1997). "An Adhesion Map for the Contact of Elastic Spheres". Journal of Colloid and Interface Science (Elsevier BV) 192 (2): 326–333. doi:10.1006/jcis.1997.4984. ISSN 0021-9797. PMID 9367554. Bibcode: 1997JCIS..192..326J.
- ↑ Zheng, Zhijun; Yu, Jilin (2007). "Using the Dugdale approximation to match a specific interaction in the adhesive contact of elastic objects". Journal of Colloid and Interface Science (Elsevier BV) 310 (1): 27–34. doi:10.1016/j.jcis.2007.01.042. ISSN 0021-9797. PMID 17335843. Bibcode: 2007JCIS..310...27Z.
- ↑ Carpick, Robert W.; Ogletree, D.Frank; Salmeron, Miquel (1999). "A General Equation for Fitting Contact Area and Friction vs Load Measurements". Journal of Colloid and Interface Science (Elsevier BV) 211 (2): 395–400. doi:10.1006/jcis.1998.6027. ISSN 0021-9797. PMID 10049556. Bibcode: 1999JCIS..211..395C.
- ↑ Popov, Valentin L.; Pohrt, Roman; Li, Qiang (2017-09-01). "Strength of adhesive contacts: Influence of contact geometry and material gradients" (in en). Friction 5 (3): 308–325. doi:10.1007/s40544-017-0177-3. ISSN 2223-7690.
- ↑ Friction Physics (2017-12-06). Science friction: Adhesion of complex shapes. Archived from the original on 2021-12-15. Retrieved 2018-01-02 – via YouTube.
External links
- [1]: More about contact stresses and the evolution of bearing stress equations can be found in this publication by NASA Glenn Research Center head the NASA Bearing, Gearing and Transmission Section, Erwin Zaretsky.
- [2]: A MATLAB routine to solve the linear elastic contact mechanics problem entitled; "An LCP solution of the linear elastic contact mechanics problem" is provided at the file exchange at MATLAB Central.
- [3]: Contact mechanics calculator.
- [4]: detailed calculations and formulae of JKR theory for two spheres.
- [5]: A Matlab code for Hertz contact analysis (includes line, point and elliptical cases).
- [6]: JKR, MD, and DMT models of adhesion (Matlab routines).
 |