Physics:Capillary action

From HandWiki
Short description: Ability of a liquid to flow in narrow spaces
Capillary water flow up a 225 mm-high porous brick after it was placed in a shallow tray of water. The time elapsed after first contact with water is indicated. From the weight increase, the estimated porosity is 25%.
Continuum mechanics
Laws
Conservations
Inequalities
Solid mechanics
Fluid mechanics
Fluids
Liquids
Gases
Plasma
Rheology
Smart fluids
Scientists
Capillary action of water (polar) compared to mercury (non-polar), in each case with respect to a polar surface such as glass (≡Si–OH)

Capillary action (sometimes called capillarity, capillary motion, capillary rise, capillary effect, or wicking) is the process of a liquid flowing in a narrow space without the assistance of, or even in opposition to, any external forces like gravity.

The effect can be seen in the drawing up of liquids between the hairs of a paint-brush, in a thin tube such as a straw, in porous materials such as paper and plaster, in some non-porous materials such as sand and liquefied carbon fiber, or in a biological cell.

It occurs because of intermolecular forces between the liquid and surrounding solid surfaces. If the diameter of the tube is sufficiently small, then the combination of surface tension (which is caused by cohesion within the liquid) and adhesive forces between the liquid and container wall act to propel the liquid.

Etymology

Capillary comes from the Latin word capillaris, meaning "of or resembling hair." The meaning stems from the tiny, hairlike diameter of a capillary.

History

The first recorded observation of capillary action was by Leonardo da Vinci.[1][2] A former student of Galileo, Niccolò Aggiunti, was said to have investigated capillary action.[3] In 1660, capillary action was still a novelty to the Irish chemist Robert Boyle, when he reported that "some inquisitive French Men" had observed that when a capillary tube was dipped into water, the water would ascend to "some height in the Pipe". Boyle then reported an experiment in which he dipped a capillary tube into red wine and then subjected the tube to a partial vacuum. He found that the vacuum had no observable influence on the height of the liquid in the capillary, so the behavior of liquids in capillary tubes was due to some phenomenon different from that which governed mercury barometers.[4]

Others soon followed Boyle's lead.[5] Some (e.g., Honoré Fabri,[6] Jacob Bernoulli[7]) thought that liquids rose in capillaries because air could not enter capillaries as easily as liquids, so the air pressure was lower inside capillaries. Others (e.g., Isaac Vossius,[8] Giovanni Alfonso Borelli,[9] Louis Carré,[10] Francis Hauksbee,[11] Josia Weitbrecht[12]) thought that the particles of liquid were attracted to each other and to the walls of the capillary.

Although experimental studies continued during the 18th century,[13] a successful quantitative treatment of capillary action[14] was not attained until 1805 by two investigators: Thomas Young of the United Kingdom[15] and Pierre-Simon Laplace of France.[16] They derived the Young–Laplace equation of capillary action. By 1830, the German mathematician Carl Friedrich Gauss had determined the boundary conditions governing capillary action (i.e., the conditions at the liquid-solid interface).[17] In 1871, the British physicist Sir William Thomson (later Lord Kelvin) determined the effect of the meniscus on a liquid's vapor pressure—a relation known as the Kelvin equation.[18] German physicist Franz Ernst Neumann (1798–1895) subsequently determined the interaction between two immiscible liquids.[19]

Albert Einstein's first paper, which was submitted to Annalen der Physik in 1900, was on capillarity.[20][21]

Phenomena and physics

Moderate rising damp on an internal wall
Capillary flow experiment to investigate capillary flows and phenomena aboard the International Space Station

Capillary penetration in porous media shares its dynamic mechanism with flow in hollow tubes, as both processes are resisted by viscous forces.[22] Consequently, a common apparatus used to demonstrate the phenomenon is the capillary tube. When the lower end of a glass tube is placed in a liquid, such as water, a concave meniscus forms. Adhesion occurs between the fluid and the solid inner wall pulling the liquid column along until there is a sufficient mass of liquid for gravitational forces to overcome these intermolecular forces. The contact length (around the edge) between the top of the liquid column and the tube is proportional to the radius of the tube, while the weight of the liquid column is proportional to the square of the tube's radius. So, a narrow tube will draw a liquid column along further than a wider tube will, given that the inner water molecules cohere sufficiently to the outer ones.

Examples

In the built environment, evaporation limited capillary penetration is responsible for the phenomenon of rising damp in concrete and masonry, while in industry and diagnostic medicine this phenomenon is increasingly being harnessed in the field of paper-based microfluidics.[22]

In physiology, capillary action is essential for the drainage of continuously produced tear fluid from the eye. Two canaliculi of tiny diameter are present in the inner corner of the eyelid, also called the lacrimal ducts; their openings can be seen with the naked eye within the lacrymal sacs when the eyelids are everted.

Wicking is the absorption of a liquid by a material in the manner of a candle wick. Paper towels absorb liquid through capillary action, allowing a fluid to be transferred from a surface to the towel. The small pores of a sponge act as small capillaries, causing it to absorb a large amount of fluid. Some textile fabrics are said to use capillary action to "wick" sweat away from the skin. These are often referred to as wicking fabrics, after the capillary properties of candle and lamp wicks.

Capillary action is observed in thin layer chromatography, in which a solvent moves vertically up a plate via capillary action. In this case the pores are gaps between very small particles.

Capillary action draws ink to the tips of fountain pen nibs from a reservoir or cartridge inside the pen.

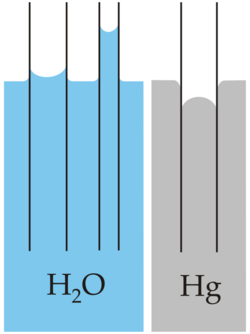
With some pairs of materials, such as mercury and glass, the intermolecular forces within the liquid exceed those between the solid and the liquid, so a convex meniscus forms and capillary action works in reverse.

In hydrology, capillary action describes the attraction of water molecules to soil particles. Capillary action is responsible for moving groundwater from wet areas of the soil to dry areas. Differences in soil potential ([math]\displaystyle{ \Psi_m }[/math]) drive capillary action in soil.

A practical application of capillary action is the capillary action siphon. Instead of utilizing a hollow tube (as in most siphons), this device consists of a length of cord made of a fibrous material (cotton cord or string works well). After saturating the cord with water, one (weighted) end is placed in a reservoir full of water, and the other end placed in a receiving vessel. The reservoir must be higher than the receiving vessel.[citation needed] A related but simplified capillary siphon only consists of two hook-shaped stainless-steel rods, whose surface is hydrophilic, allowing water to wet the narrow grooves between them.[23] Due to capillary action and gravity, water will slowly transfer from the reservoir to the receiving vessel. This simple device can be used to water houseplants when nobody is home. This property is also made use of in the lubrication of steam locomotives: wicks of worsted wool are used to draw oil from reservoirs into delivery pipes leading to the bearings.[24]

In plants and animals

Capillary action is seen in many plants, and plays a part in transpiration. Water is brought high up in trees by branching; evaporation at the leaves creating depressurization; probably by osmotic pressure added at the roots; and possibly at other locations inside the plant, especially when gathering humidity with air roots.[25][26][27]

Capillary action for uptake of water has been described in some small animals, such as Ligia exotica[28] and Moloch horridus.[29]

Height of a meniscus

Capillary rise of liquid in a capillary

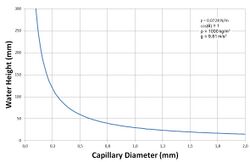
Water height in a capillary plotted against capillary diameter

The height h of a liquid column is given by Jurin's law[30]

[math]\displaystyle{ h={{2 \gamma \cos{\theta}}\over{\rho g r}}, }[/math]

where [math]\displaystyle{ \scriptstyle \gamma }[/math] is the liquid-air surface tension (force/unit length), θ is the contact angle, ρ is the density of liquid (mass/volume), g is the local acceleration due to gravity (length/square of time[31]), and r is the radius of tube.

As r is in the denominator, the thinner the space in which the liquid can travel, the further up it goes. Likewise, lighter liquid and lower gravity increase the height of the column.

For a water-filled glass tube in air at standard laboratory conditions, γ = 0.0728 N/m at 20 °C, ρ = 1000 kg/m3, and g = 9.81 m/s2. Because water spreads on clean glass, the effective equilibrium contact angle is approximately zero.[32] For these values, the height of the water column is

[math]\displaystyle{ h\approx {{1.48 \times 10^{-5} \ \mbox{m}^2}\over r}. }[/math]

Thus for a 2 m (6.6 ft) radius glass tube in lab conditions given above, the water would rise an unnoticeable 0.007 mm (0.00028 in). However, for a 2 cm (0.79 in) radius tube, the water would rise 0.7 mm (0.028 in), and for a 0.2 mm (0.0079 in) radius tube, the water would rise 70 mm (2.8 in).

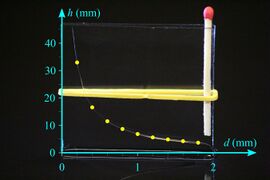
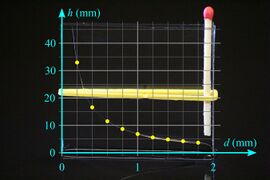
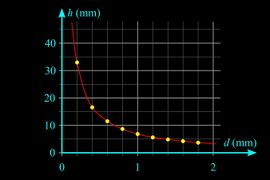
Capillary rise of liquid between two glass plates

The product of layer thickness (d) and elevation height (h) is constant (d·h = constant), the two quantities are inversely proportional. The surface of the liquid between the planes is hyperbola.

  • Water between two glass plates
  • Kapilláris emelkedés 1.jpg
  • Kapilláris emelkedés 2.jpg
  • Kapilláris emelkedés 3.jpg
  • Kapilláris emelkedés 4.jpg
  • Kapilláris emelkedés 5.jpg
  • Kapilláris emelkedés 6.jpg

Liquid transport in porous media

Capillary flow in a brick, with a sorptivity of 5.0 mm·min−1/2 and a porosity of 0.25.

When a dry porous medium is brought into contact with a liquid, it will absorb the liquid at a rate which decreases over time. When considering evaporation, liquid penetration will reach a limit dependent on parameters of temperature, humidity and permeability. This process is known as evaporation limited capillary penetration [22] and is widely observed in common situations including fluid absorption into paper and rising damp in concrete or masonry walls. For a bar shaped section of material with cross-sectional area A that is wetted on one end, the cumulative volume V of absorbed liquid after a time t is

[math]\displaystyle{ V = AS\sqrt{t}, }[/math]

where S is the sorptivity of the medium, in units of m·s−1/2 or mm·min−1/2. This time dependence relation is similar to Washburn's equation for the wicking in capillaries and porous media.[33] The quantity

[math]\displaystyle{ i = \frac{V}{A} }[/math]

is called the cumulative liquid intake, with the dimension of length. The wetted length of the bar, that is the distance between the wetted end of the bar and the so-called wet front, is dependent on the fraction f of the volume occupied by voids. This number f is the porosity of the medium; the wetted length is then

[math]\displaystyle{ x = \frac{i}{f} = \frac{S}{f}\sqrt{t}. }[/math]

Some authors use the quantity S/f as the sorptivity.[34] The above description is for the case where gravity and evaporation do not play a role.

Sorptivity is a relevant property of building materials, because it affects the amount of rising dampness. Some values for the sorptivity of building materials are in the table below.

Sorptivity of selected materials (source:[35])
Material Sorptivity
(mm·min−1/2)
Aerated concrete 0.50
Gypsum plaster 3.50
Clay brick 1.16
Mortar 0.70
Concrete brick 0.20

See also

References

  1. ↑ See:
    • Manuscripts of Léonardo de Vinci (Paris), vol. N, folios 11, 67, and 74.
    • Guillaume Libri, Histoire des sciences mathématiques en Italie, depuis la Renaissance des lettres jusqu'a la fin du dix-septième siecle [History of the mathematical sciences in Italy, from the Renaissance until the end of the seventeenth century] (Paris, France: Jules Renouard et cie., 1840), vol. 3, page 54 . From page 54: "Enfin, deux observations capitales, celle de l'action capillaire (7) et celle de la diffraction (8), dont jusqu'à présent on avait méconnu le véritable auteur, sont dues également à ce brillant génie." (Finally, two major observations, that of capillary action (7) and that of diffraction (8), the true author of which until now had not been recognized, are also due to this brilliant genius.)
    • C. Wolf (1857) "Vom Einfluss der Temperatur auf die Erscheinungen in Haarröhrchen" (On the influence of temperature on phenomena in capillary tubes) Annalen der Physik und Chemie, 101 (177) : 550–576; see footnote on page 551 by editor Johann C. Poggendorff. From page 551: " ... nach Libri (Hist. des sciences math. en Italie, T. III, p. 54) in den zu Paris aufbewahrten Handschriften des grossen Künstlers Leonardo da Vinci (gestorben 1519) schon Beobachtungen dieser Art vorfinden; ... " ( ... according to Libri (History of the mathematical sciences in Italy, vol. 3, p. 54) observations of this kind [i.e., of capillary action] are already to be found in the manuscripts of the great artist Leonardo da Vinci (died 1519), which are preserved in Paris; ... )
  2. ↑ More detailed histories of research on capillary action can be found in:
  3. ↑ In his book of 1759, Giovani Batista Clemente Nelli (1725–1793) stated (p. 87) that he had "un libro di problem vari geometrici ec. e di speculazioni, ed esperienze fisiche ec." (a book of various geometric problems and of speculation and physical experiments, etc.) by Aggiunti. On pages 91–92, he quotes from this book: Aggiunti attributed capillary action to "moto occulto" (hidden/secret motion). He proposed that mosquitoes, butterflies, and bees feed via capillary action, and that sap ascends in plants via capillary action. See: Giovambatista Clemente Nelli, Saggio di Storia Letteraria Fiorentina del Secolo XVII ... [Essay on Florence's literary history in the 17th century, ... ] (Lucca, (Italy): Vincenzo Giuntini, 1759), pp. 91–92.
  4. ↑ Robert Boyle, New Experiments Physico-Mechanical touching the Spring of the Air, ... (Oxford, England: H. Hall, 1660), pp. 265–270. Available on-line at: Echo (Max Planck Institute for the History of Science; Berlin, Germany) .
  5. ↑ See, for example:
    • Robert Hooke (1661) An attempt for the explication of the Phenomena observable in an experiment published by the Right Hon. Robert Boyle, in the 35th experiment of his Epistolical Discourse touching the Air, in confirmation of a former conjecture made by R. Hooke. [pamphlet].
    • Hooke's An attempt for the explication ... was reprinted (with some changes) in: Robert Hooke, Micrographia ... (London, England: James Allestry, 1667), pp. 12–22, "Observ. IV. Of small Glass Canes."
    • Geminiano Montanari, Pensieri fisico-matematici sopra alcune esperienze fatte in Bologna ... [Physical-mathematical ideas about some experiments done in Bologna ... ] (Bologna, (Italy): 1667).
    • George Sinclair, Ars Nova et Magna Gravitatis et Levitatis [New and great powers of weight and levity] (Rotterdam, Netherlands: Arnold Leers, Jr., 1669).
    • Johannes Christoph Sturm, Collegium Experimentale sive Curiosum [Catalog of experiments, or Curiosity] (Nüremberg (Norimbergæ), (Germany): Wolfgang Moritz Endter & the heirs of Johann Andreas Endter, 1676). See: "Tentamen VIII. Canaliculorum angustiorum recens-notata Phænomena, ... " (Essay 8. Recently noted phenomena of narrow capillaries, ... ), pp. 44–48.
  6. ↑ See:
    • Honorato Fabri, Dialogi physici ... ((Lyon (Lugdunum), France: 1665), pages 157 ff "Dialogus Quartus. In quo, de libratis suspensisque liquoribus & Mercurio disputatur. (Dialogue four. In which the balance and suspension of liquids and mercury is discussed).
    • Honorato Fabri, Dialogi physici ... ((Lyon (Lugdunum), France: Antoine Molin, 1669), pages 267 ff "Alithophilus, Dialogus quartus, in quo nonnulla discutiuntur à D. Montanario opposita circa elevationem Humoris in canaliculis, etc." (Alithophilus, Fourth dialogue, in which Dr. Montanari's opposition regarding the elevation of liquids in capillaries is utterly refuted).
  7. ↑ Jacob Bernoulli, Dissertatio de Gravitate Ætheris (Amsterdam, Netherlands: Hendrik Wetsten, 1683).
  8. ↑ Isaac Vossius, De Nili et Aliorum Fluminum Origine [On the sources of the Nile and other rivers] (Hague (Hagæ Comitis), Netherlands: Adrian Vlacq, 1666), pages 3–7 (chapter 2).
  9. ↑ Borelli, Giovanni Alfonso De motionibus naturalibus a gravitate pendentibus (Lyon, France: 1670), page 385, Cap. 8 Prop. CLXXXV (Chapter 8, Proposition 185.). Available on-line at: Echo (Max Planck Institute for the History of Science; Berlin, Germany) .
  10. ↑ Carré (1705) "Experiences sur les tuyaux Capillaires" (Experiments on capillary tubes), Mémoires de l'Académie Royale des Sciences, pp. 241–254.
  11. ↑ See:
  12. ↑ See:
  13. ↑ For example:
    • In 1740, Christlieb Ehregott Gellert (1713–1795) observed that like mercury, molten lead would not adhere to glass and therefore the level of molten lead was depressed in a capillary tube. See: C. E. Gellert (1740) "De phenomenis plumbi fusi in tubis capillaribus" (On phenomena of molten lead in capillary tubes) Commentarii academiae scientiarum imperialis Petropolitanae (Memoirs of the imperial academy of sciences in St. Petersburg), 12 : 243–251. Available on-line at: Archive.org .
    • Gaspard Monge (1746–1818) investigated the force between panes of glass that were separated by a film of liquid. See: Gaspard Monge (1787) "Mémoire sur quelques effets d'attraction ou de répulsion apparente entre les molécules de matière" (Memoir on some effects of the apparent attraction or repulsion between molecules of matter), Histoire de l'Académie royale des sciences, avec les Mémoires de l'Académie Royale des Sciences de Paris (History of the Royal Academy of Sciences, with the Memoirs of the Royal Academy of Sciences of Paris), pp. 506–529. Monge proposed that particles of a liquid exert, on each other, a short-range force of attraction, and that this force produces the surface tension of the liquid. From p. 529: "En supposant ainsi que l'adhérence des molécules d'un liquide n'ait d'effet sensible qu'à la surface même, & dans le sens de la surface, il seroit facile de déterminer la courbure des surfaces des liquides dans le voisinage des parois qui les conteinnent; ces surfaces seroient des lintéaires dont la tension, constante dans tous les sens, seroit par-tout égale à l'adhérence de deux molécules; & les phénomènes des tubes capillaires n'auroient plus rein qui ne pût être déterminé par l'analyse." (Thus by assuming that the adhesion of a liquid's molecules has a significant effect only at the surface itself, and in the direction of the surface, it would be easy to determine the curvature of the surfaces of liquids in the vicinity of the walls that contain them; these surfaces would be menisci whose tension, [being] constant in every direction, would be everywhere equal to the adhesion of two molecules; and the phenomena of capillary tubes would have nothing that could not be determined by analysis [i.e., calculus].)
  14. ↑ In the 18th century, some investigators did attempt a quantitative treatment of capillary action. See, for example, Alexis Claude Clairaut (1713–1765) Theorie de la Figure de la Terre tirée des Principes de l'Hydrostatique [Theory of the figure of the Earth based on principles of hydrostatics] (Paris, France: David fils, 1743), Chapitre X. De l'élevation ou de l'abaissement des Liqueurs dans les Tuyaux capillaires (Chapter 10. On the elevation or depression of liquids in capillary tubes), pages 105–128.
  15. ↑ Thomas Young (January 1, 1805) "An essay on the cohesion of fluids," Philosophical Transactions of the Royal Society of London, 95 : 65–87.
  16. ↑ Pierre Simon marquis de Laplace, Traité de Mécanique Céleste, volume 4, (Paris, France: Courcier, 1805), Supplément au dixième livre du Traité de Mécanique Céleste, pages 1–79 .
  17. ↑ Carl Friedrich Gauss, Principia generalia Theoriae Figurae Fluidorum in statu Aequilibrii [General principles of the theory of fluid shapes in a state of equilibrium] (Göttingen, (Germany): Dieterichs, 1830). Available on-line at: Hathi Trust.
  18. ↑ William Thomson (1871) "On the equilibrium of vapour at a curved surface of liquid," Philosophical Magazine, series 4, 42 (282) : 448–452.
  19. ↑ Franz Neumann with A. Wangerin, ed., Vorlesungen über die Theorie der Capillarität [Lectures on the theory of capillarity] (Leipzig, Germany: B. G. Teubner, 1894).
  20. ↑ Albert Einstein (1901) "Folgerungen aus den Capillaritätserscheinungen" (Conclusions [drawn] from capillary phenomena), Annalen der Physik, 309 (3) : 513–523.
  21. ↑ Hans-Josef Kuepper. "List of Scientific Publications of Albert Einstein". Einstein-website.de. http://www.einstein-website.de/z_physics/wisspub-e.html. 
  22. ↑ 22.0 22.1 22.2 Liu, Mingchao; Wu, Jian; Gan, Yixiang; Hanaor, Dorian A.H.; Chen, C.Q. (2018). "Tuning capillary penetration in porous media: Combining geometrical and evaporation effects". International Journal of Heat and Mass Transfer 123: 239–250. doi:10.1016/j.ijheatmasstransfer.2018.02.101. http://drgan.org/wp-content/uploads/2018/03/051_IJHMT_2018.pdf. 
  23. ↑ Wang, K. (2022). "Open Capillary Siphons". Journal of Fluid Mechanics (Cambridge University Press) 932. doi:10.1017/jfm.2021.1056. Bibcode: 2022JFM...932R...1W. 
  24. ↑ Ahrons, Ernest Leopold (1922). Lubrication of Locomotives. London: Locomotive Publishing Company. p. 26. OCLC 795781750. 
  25. ↑ Tree physics at "Neat, Plausible And" scientific discussion website.
  26. ↑ Water in Redwood and other trees, mostly by evaporation article at wonderquest website.
  27. ↑ Poudel, Sajag; Zou, An; Maroo, Shalabh C. (2022-06-15). "Disjoining pressure driven transpiration of water in a simulated tree" (in en). Journal of Colloid and Interface Science 616: 895–902. doi:10.1016/j.jcis.2022.02.108. ISSN 0021-9797. PMID 35259719. https://www.sciencedirect.com/science/article/pii/S0021979722003393. 
  28. ↑ "Water transport mechanism through open capillaries analyzed by direct surface modifications on biological surfaces". Scientific Reports 3: 3024. October 23, 2013. doi:10.1038/srep03024. PMID 24149467. Bibcode: 2013NatSR...3E3024I. 
  29. ↑ "Uptake of water by the lizard, Moloch horridus". Nature 194 (4829): 699–670 (1962). 1962. doi:10.1038/194699a0. PMID 13867381. Bibcode: 1962Natur.194..699B. 
  30. ↑ G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967) ISBN:0-521-66396-2,
  31. ↑ Hsai-Yang Fang, john L. Daniels, Introductory Geotechnical Engineering: An Environmental Perspective
  32. ↑ "Capillary Tubes - an overview | ScienceDirect Topics". https://www.sciencedirect.com/topics/earth-and-planetary-sciences/capillary-tubes. 
  33. ↑ Liu, M. (2016). "Evaporation limited radial capillary penetration in porous media". Langmuir 32 (38): 9899–9904. doi:10.1021/acs.langmuir.6b02404. PMID 27583455. http://drgan.org/wp-content/uploads/2014/07/040_Langmuir_2016.pdf. 
  34. ↑ C. Hall, W.D. Hoff, Water transport in brick, stone, and concrete. (2002) page 131 on Google books
  35. ↑ Hall and Hoff, p. 122

Further reading



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Capillary_action&oldid=3279348"