Physics:Dicke model

From HandWiki
Revision as of 02:51, 5 February 2024 by Scavis2 (talk | contribs) (correction)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Model of quantum optics

The Dicke model is a fundamental model of quantum optics, which describes the interaction between light and matter. In the Dicke model, the light component is described as a single quantum mode, while the matter is described as a set of two-level systems. When the coupling between the light and matter crosses a critical value, the Dicke model shows a mean-field phase transition to a superradiant phase. This transition belongs to the Ising universality class and was realized in cavity quantum electrodynamics experiments. Although the superradiant transition bears some analogy with the lasing instability, these two transitions belong to different universality classes.

Description

The Dicke model is a quantum mechanical model that describes the coupling between a single-mode cavity and [math]\displaystyle{ N }[/math] two-level systems, or equivalently [math]\displaystyle{ N }[/math] spin-½ degrees of freedom. The model was first introduced in 1973 by K. Hepp and E. H. Lieb.[1] Their study was inspired by the pioneering work of R. H. Dicke on the superradiant emission of light in free space [2] and named after him.

Like any other model in quantum mechanics, the Dicke model includes a set of quantum states (the Hilbert space) and a total-energy operator (the Hamiltonian). The Hilbert space of the Dicke model is given by (the tensor product of) the states of the cavity and of the two-level systems. The Hilbert space of the cavity can be spanned by Fock states with [math]\displaystyle{ n }[/math] photons, denoted by [math]\displaystyle{ |n\rangle }[/math]. These states can be constructed from the vacuum state [math]\displaystyle{ |n=0\rangle }[/math] using the canonical ladder operators, [math]\displaystyle{ a^\dagger }[/math] and [math]\displaystyle{ a }[/math], which add and subtract a photon from the cavity, respectively. The states of each two-level system are referred to as up and down and are defined through the spin operators [math]\displaystyle{ \vec\sigma_j = (\sigma^x_j,~\sigma^y_j,~\sigma^z_j) }[/math], satisfying the spin algebra [math]\displaystyle{ [\sigma^x_j,~\sigma^y_k]=i\hbar\sigma^z_j\delta_{j,k} }[/math]. Here [math]\displaystyle{ \hbar }[/math] is the Planck constant and [math]\displaystyle{ j = (0,1,2,...,N) }[/math] indicates a specific two-level system.[3]

The Hamiltonian of the Dicke model is

[math]\displaystyle{ H = \hbar\omega_c a^\dagger a +\omega_z \sum_{j=1}^N \sigma^z_j +\frac{2\lambda}{\sqrt{N}} (a+a^\dagger) \sum_j \sigma^x_j\;. }[/math]

 

 

 

 

(1)

Here, the first term describes the energy of the cavity and equals to the product of the energy of a single cavity photon [math]\displaystyle{ \hbar\omega_c }[/math] (where [math]\displaystyle{ \omega_c }[/math] is the cavity frequency), times the number of photons in the cavity, [math]\displaystyle{ n_c=a^\dagger a }[/math]. The second term describes the energy of the two-level systems, where [math]\displaystyle{ \hbar\omega_z }[/math] is the energy difference between the states of each two-level system. The last term describes the coupling between the two-level systems and the cavity and is assumed to be proportional to a constant, [math]\displaystyle{ \lambda }[/math], times the inverse of the square root of the number of two-level systems. This assumption allows one to obtain a phase transition in the limit of [math]\displaystyle{ N\to\infty }[/math] (see below). The coupling can be written as the sum of two terms: a co-rotating term that conserves the number of excitations and is proportional to [math]\displaystyle{ a \sigma^+ + a^\dagger \sigma^- }[/math] and a counter-rotating term proportional to [math]\displaystyle{ a \sigma^- + a^\dagger \sigma^+ }[/math], where [math]\displaystyle{ \sigma^\pm = \sigma^x \pm i \sigma^y }[/math] are the spin ladder operators.

The Hamiltonian in Eq. 1 assumes that all the spins are identical (i.e. have the same energy difference and are equally coupled to the cavity). Under this assumption, one can define the macroscopic spin operators [math]\displaystyle{ S^\alpha=\sum_{j=1}^N\sigma_j^\alpha }[/math], with [math]\displaystyle{ \alpha=x,y,z }[/math], which satisfy the spin algebra, [math]\displaystyle{ [S^x,S^y]=i\hbar S^z }[/math]. Using these operators, one can rewrite the Hamiltonian in Eq. 1 as

[math]\displaystyle{ H=\hbar\omega_c a^\dagger a+\omega_z S^z+\frac{2\lambda}{\sqrt{N}}(a+a^\dagger)S^x. }[/math]

 

 

 

 

(2)

This notation simplifies the numerical study of the model because it involves a single spin-S with [math]\displaystyle{ S\leq N/2 }[/math], whose Hilbert space has size [math]\displaystyle{ 2S+1 }[/math], rather than [math]\displaystyle{ N }[/math] spin-1/2, whose Hilbert space has size [math]\displaystyle{ 2^N }[/math].

The Dicke model has one global symmetry,

[math]\displaystyle{ \mathcal{P} : (a,\sigma^\pm ) \to (-a,-\sigma^\pm)\;. }[/math]

 

 

 

 

(3)

Because [math]\displaystyle{ \mathcal{P} }[/math] squares to unity (i.e. if applied twice, it brings each state back to its original state), it has two eigenvalues, [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ -1 }[/math]. This symmetry is associated with a conserved quantity: the parity of the total number of excitations, [math]\displaystyle{ P=(-1)^{N_{ex}} }[/math], where

[math]\displaystyle{ N_{ex}=a^\dagger a + \sum_{j=1}^N\sigma^z_j\;. }[/math]

 

 

 

 

(4)

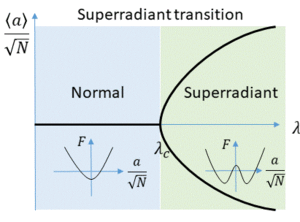
This parity conservation can be seen from the fact that each term in the Hamiltonian preserves the excitation number, except for the counter-rotating terms, which can only change the excitation number by [math]\displaystyle{ \pm 2 }[/math]. A state of the Dicke model is said to be normal when this symmetry is preserved, and superradiant when this symmetry is spontaneously broken.

Related models

The Dicke model is closely related to other models of quantum optics. Specifically, the Dicke model with a single two-level system, [math]\displaystyle{ N=1 }[/math], is called the Rabi model. In the absence of counter-rotating terms, the model is called Jaynes-Cummings for [math]\displaystyle{ N=1 }[/math] and Tavis-Cummings for [math]\displaystyle{ N\gt 1 }[/math]. These two models conserve the number of excitations [math]\displaystyle{ N_{ex} }[/math] and are characterized by a [math]\displaystyle{ U(1) }[/math] symmetry. The spontaneous breaking of this symmetry gives rise to a lasing state (see below).

The relation between the Dicke model and other models is summarized in the table below [4]

Model's name Counter-rotating terms? symmetry Number of two-level systems
Jaynes-Cummings no [math]\displaystyle{ U(1) }[/math] [math]\displaystyle{ N = 1 }[/math]
Tavis-Cummings no [math]\displaystyle{ U(1) }[/math] [math]\displaystyle{ N \gt 1 }[/math]
Rabi model yes [math]\displaystyle{ \mathcal{P} }[/math] [math]\displaystyle{ N = 1 }[/math]
Dicke yes [math]\displaystyle{ \mathcal{P} }[/math] [math]\displaystyle{ N \gt 1 }[/math]

Superradiant phase transition

Schematic plot of the order parameter of the Dicke transition, which is zero in the normal phase and finite in the superradiant phase. The inset shows the free energy in the normal and superradiant phases, see Eq. 5.

Early studies of the Dicke model considered its equilibrium properties.[1] These works considered the limit of [math]\displaystyle{ N\to\infty }[/math] (also known as the thermodynamic limit) and assumed a thermal partition function, [math]\displaystyle{ Z=\exp(-H/k_B T) }[/math], where [math]\displaystyle{ k_B }[/math] is the Boltzmann constant and [math]\displaystyle{ T }[/math] is the temperature. It was found that, when the coupling [math]\displaystyle{ \lambda }[/math] crosses a critical value [math]\displaystyle{ \lambda_c }[/math], the Dicke model undergoes a second-order phase transition, known as the superradiant phase transition. In their original derivation, Hepp and Lieb[1] neglected the effects of counter-rotating terms and, thus, actually considered the Tavis-Cummings model (see above). Further studies of the full Dicke model found that the phase transition still occurs in the presence of counter-rotating terms, albeit at a different critical coupling.[5]

The superradiant transition spontaneously breaks the parity symmetry, [math]\displaystyle{ \mathcal{P} }[/math], defined in Eq. 3. The order parameter of this phase transition is [math]\displaystyle{ \langle{a}\rangle/\sqrt{N} }[/math]. In the thermodynamic limit, this quantity tends to zero if the system is normal, or to one of two possible values, if the system is superradiant. These two values correspond to physical states of the cavity field with opposite phases (see Eq. 3 and, correspondingly, to states of the spin with opposite [math]\displaystyle{ x }[/math] components). Close to the superradiant phase transition, the order parameter depends on [math]\displaystyle{ \lambda }[/math] as [math]\displaystyle{ \langle{a}\rangle/\sqrt{N}\sim(\lambda_c-\lambda)^{-1/2} }[/math]. This dependence corresponds to the mean-field critical exponent [math]\displaystyle{ \beta = 1/2 }[/math].

Mean-field description of the transition

The simplest way to describe the superradiant transition is to use a mean-field approximation, in which the cavity field operators are substituted by their expectation values. Under this approximation, which is exact in the thermodynamic limit, the Dicke Hamiltonian of Eq. 1 becomes a sum of independent terms, each acting on a different two-level system, which can be diagonalized independently. At thermal equilibrium (see above), one finds that the free energy per two-level system is[6]

[math]\displaystyle{ F\left(\frac{\langle a\rangle}{\sqrt{N}}=\alpha\right) = \omega_c \alpha^2 - k_B T \ln\left(2 \cosh\left(\frac{\sqrt{\omega_z^2+16\lambda^2\alpha^2}}{2k_B T}\right)\right). }[/math]

 

 

 

 

(5)

The critical coupling of the transition can be found by the condition [math]\displaystyle{ dF/d\alpha(\alpha=0)=0 }[/math], leading to

[math]\displaystyle{ \lambda_c = \frac12\sqrt{\omega_c \omega_z\coth\left(\frac{\hbar\omega_z}{2k_BT}\right)}. }[/math]

 

 

 

 

(6)

For [math]\displaystyle{ \lambda\lt \lambda_c }[/math], [math]\displaystyle{ F }[/math] has one minimum, while for [math]\displaystyle{ \lambda\gt \lambda_c }[/math], it has two minima. In the limit of [math]\displaystyle{ T\to0 }[/math] one obtains an expression for the critical coupling of the zero-temperature superradiant phase transition, [math]\displaystyle{ \lambda_c=\sqrt{\omega_c\omega_z}/2 }[/math].

Semiclassical limit and chaos

Semiclassical limit

A phase space for the Dicke model in the symmetric atomic subspace with [math]\displaystyle{ S=N/2 }[/math] may be constructed by considering the tensor product of the Glauber coherent states

[math]\displaystyle{ \left \vert q,p\right \rangle=D(q,p)\left\vert 0\right \rangle, }[/math]

 

 

 

 

(7)

where [math]\displaystyle{ D(q,p)=e^{-\frac{S}{4}\left (q^2 + p^2\right)}\exp\left(\sqrt{\frac{S}{2} }\left(q+ip\right) a^\dagger\right) }[/math] is the displacement operator and [math]\displaystyle{ \left\vert 0\right \rangle }[/math] is the photon vacuum Fock state, and the SU(2) coherent states

[math]\displaystyle{ \left \vert Q,P\right \rangle=R(Q,P)\left\vert S,-S\right \rangle, }[/math]

 

 

 

 

(8)

where [math]\displaystyle{ R(Q,P)=\left(1-\frac{Q^2+P^2}{4}\right)^S \exp\left(\sqrt{\frac{1}{4-Q^2-P^2}}\left(Q+iP\right) \frac{S^+}{\hbar}\right) }[/math] is the rotation operator in the Bloch sphere, [math]\displaystyle{ Q^2+P^2 \leq 4, }[/math] and [math]\displaystyle{ \left \vert {S,-S}\right \rangle }[/math] is the state with all atoms in their ground state. This yields a four-dimensional phase space with canonical coordinates [math]\displaystyle{ (q,p) }[/math] and [math]\displaystyle{ (Q,P) }[/math].

A classical Hamiltonian is obtained by taking the expectation value of the Dicke Hamiltonian given by Eq. 2 under these states,[7][8]

[math]\displaystyle{ H_\text{cl}(q,p,Q,P)=\frac{\hbar S\omega_c}{2}\left(q^2 + p^2\right) + \frac{\hbar S \omega_z }{2}\left(Q^2+P^2\right) + 2\hbar S \lambda\, Q q \sqrt{1-\frac{Q^2+P^2}{4} } - \hbar S\omega_z. }[/math]

 

 

 

 

(9)

Percentage of classical trajectories with positive Lyapunov exponent as a function of the energy per particle [math]\displaystyle{ E/S }[/math] and the coupling parameter [math]\displaystyle{ \lambda }[/math] (divided by the critical coupling [math]\displaystyle{ \lambda_c=\sqrt{\omega_c\omega_z}/2 }[/math]). The parameters are [math]\displaystyle{ \omega_c=\omega_z=1 }[/math].

In the limit of [math]\displaystyle{ N\to \infty }[/math], the quantum dynamics given by the quantum Hamiltonian of Eq. 2 and the classical dynamics given by Eq. 9 coincide. For a finite system size, there is a classical and quantum correspondence that breaks down at the Ehrenfest time, which is inversely proportional to [math]\displaystyle{ N }[/math].

Quantum chaos

The Dicke model provides an ideal system to study the quantum-classical correspondence and quantum chaos.[9]

The classical system given by Eq. 9 is chaotic or regular depending on the values of the parameters [math]\displaystyle{ \lambda }[/math], [math]\displaystyle{ \omega_c }[/math], and [math]\displaystyle{ \omega_z }[/math] and the energy [math]\displaystyle{ E }[/math].[8][10] Note that there may be chaos in both the normal and superradadiant regimes.

It was recently found that the exponential growth rate of the out-of-time-order correlator coincides with the classical Lyapunov exponents[11][12] in the chaotic regime and at unstable points of the regular regime. In addition, the evolution of the survival probability (i.e. the fidelity of a state with itself at a later time) of initial coherent states highly delocalized in the energy eigenbasis is well-described by random matrix theory,[13][14] while initial coherent states strongly affected by the presence of quantum scars display behaviors that break ergodicity.[15][16]

Open Dicke model

The Dicke model of Eq. 1 assumes that the cavity mode and the two-level systems are perfectly isolated from the external environment. In actual experiments, this assumption is not valid: the coupling to free modes of light can cause the loss of cavity photons and the decay of the two-level systems (i.e. dissipation channels). It is worth mentioning, that these experiments use driving fields (e.g. laser fields) to implement the coupling between the cavity mode and the two-level systems. The various dissipation channels can be described by adding a coupling to additional environmental degrees of freedom. By averaging over the dynamics of these external degrees of freedom one obtains equations of motion describing an open quantum system. According to the common Born-Markov approximation, one can describe the dynamics of the system with the quantum master equation in Lindblad form [17]

[math]\displaystyle{ \frac{d\rho}{dt}=-{i\over\hbar}[H,\rho]+\sum_{\alpha}\gamma_\alpha\left(L_\alpha\rho L_\alpha^\dagger-\frac{1}{2}\left\{L_\alpha^\dagger L_\alpha, \rho\right\}\right). }[/math]

 

 

 

 

(10)

Here, [math]\displaystyle{ \rho }[/math] is the density matrix of the system, [math]\displaystyle{ L_\alpha }[/math] is the Lindblad operator of the decay channel [math]\displaystyle{ \alpha }[/math], and [math]\displaystyle{ \gamma_\alpha }[/math] the associated decay rate. When the Hamiltonian [math]\displaystyle{ H }[/math] is given by Eq. 1, the model is referred to as the open Dicke model.

Some common decay processes that are relevant to experiments are given in the following table:

- Cavity decay Atomic decay Atomic dephasing Collective decay
Lindbladian [math]\displaystyle{ L=a }[/math] [math]\displaystyle{ L=\sigma^-_i }[/math] [math]\displaystyle{ L=\sigma^z_i }[/math] [math]\displaystyle{ L = \sum_i \sigma_i^- }[/math]
Decay rate [math]\displaystyle{ \kappa }[/math] [math]\displaystyle{ \gamma_\downarrow }[/math] [math]\displaystyle{ \gamma_\phi }[/math] [math]\displaystyle{ \Gamma_\downarrow }[/math]

In the theoretical description of the model, one often considers the steady state where [math]\displaystyle{ d\rho/dt = 0 }[/math]. In the limit of [math]\displaystyle{ N\to\infty }[/math], the steady state of the open Dicke model shows a continuous phase transition, often referred to as the nonequilibrium superradiant transition. The critical exponents of this transition are the same as the equilibrium superradiant transition at finite temperature (and differ from the superradiant transition at zero temperature).

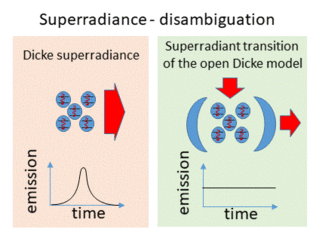
Superradiant transition and Dicke superradiance

Schematic representation of the difference between Dicke superradiance and the superradiant transition of the open Dicke model.

The superradiant transition of the open Dicke model is related to, but differs from, Dicke superradiance.

Dicke superradiance is a collective phenomenon in which many two-level systems emit photons coherently in free space.[2][18] It occurs if the two-level systems are initially prepared in their excited state and placed at a distance much smaller than the relevant photon's wavelength. Under these conditions, the spontaneous decay of the two-level systems becomes much faster: the two-level systems emit a short pulse of light with large amplitude. Under ideal conditions, the pulse duration is inversely proportional to the number of two-level systems, [math]\displaystyle{ N }[/math], and the maximal intensity of the emitted light scales as [math]\displaystyle{ N^2 }[/math]. This is in contrast to the spontaneous emission of [math]\displaystyle{ N }[/math] independent two-level systems, whose decay time does not depend on [math]\displaystyle{ N }[/math] and where the pulse intensity scales as [math]\displaystyle{ N }[/math].

As explained above, the open Dicke model rather models two-level systems coupled to a quantized cavity and driven by an external pump. In the normal phase, the intensity of the cavity field does not scale with the number of atoms [math]\displaystyle{ N }[/math], while in the superradiant phase, the intensity of the cavity field is proportional to [math]\displaystyle{ \langle a^\dagger a \rangle \sim N }[/math].

The scaling laws of Dicke superradiance and of the superradiant transition of the Dicke model are summarized in the following table:

Dicke superradiance[2] Superradiant transition of the Dicke model[1]
Environment Free space Cavity
Duration Transient Steady state
Intensity of the field (normal) [math]\displaystyle{ N }[/math] [math]\displaystyle{ 1 }[/math]
Intensity of the field (superradiant) [math]\displaystyle{ N^2 }[/math] [math]\displaystyle{ N }[/math]

Experimental realizations

Schematic representation of two schemes to experimentally realize the Dicke model: on the left, the equilibrium approach based on the dipole coupling between the two levels and, on the right, the nonequilibrium approach based on two-photon processes, namely stimulated Raman scattering. Only the latter scheme is used to realize the Dicke model.

The simplest realization of the Dicke model involves the dipole coupling between two-level atoms in a cavity. In this system, the observation of the superradiant transition is hindered by two possible problems: (1) The bare coupling between atoms and cavities is usually weak and insufficient to reach the critical value [math]\displaystyle{ \lambda_c }[/math], see Eq. 6.[19] (2) An accurate modelling of the physical system requires to consider [math]\displaystyle{ A^2 }[/math] terms that according to a no-go theorem, may prevent the transition. Both limitations can be circumvented by applying external pumps on the atoms and creating an effective Dicke model in an appropriately rotating frame.[20][21]

In 2010, the superradiant transition of the open Dicke model was observed experimentally using neutral Rubidium atoms trapped in an optical cavity.[22] In these experiments, the coupling between the atoms and the cavity is not achieved by a direct dipole coupling between the two systems. Instead, the atoms are illuminated by an external pump, which drives a stimulated Raman transition. This two-photon process causes the two-level system to change its state from down to up, or vice versa, and emit or absorb a photon into the cavity. Experiments showed that the number of photons in the cavity shows a steep increase when the pump intensity crosses a critical threshold. This threshold was associated with the critical coupling of the Dicke model.

In the experiments, two different sets of physical states were used as the down and up states. In some experiments,[23][22][24] the two states correspond to atoms with different velocities, or momenta: the down state had zero momentum and belonged to a Bose-Einstein condensate, while the up state had a momentum equal to sum of the momentum of a cavity photon and the momentum of a pump photon.[25] [26] In contrast, later experiments[27][28] used two different hyperfine levels of the Rubidium atoms in a magnetic field. The latter realization allowed the researchers to study a generalized Dicke model (see below). In both experiments, the system is time-dependent and the (generalized) Dicke Hamiltonian is realized in a frame that rotates at the pump's frequency.

Generalized model and lasing

The Dicke model can be generalized by considering the effects of additional terms in the Hamiltonian of Eq. 1.[6] For example, a recent experiment[28] realized an open Dicke model with independently tunable rotating and counter-rotating terms. In addition to the superradiant transition, this generalized Dicke model can undergo a lasing instability, which was termed inverted lasing or counter-lasing.[6] This transition is induced by the counter-rotating terms of the Dicke model and is most prominent when these terms are larger than the rotating ones.

The nonequilibrium superradiant transition and the lasing instability have several similarities and differences. Both transitions are of a mean-field type and can be understood in terms of the dynamics of a single degree of freedom. The superradiant transition corresponds to a supercritical pitchfork bifurcation, while the lasing instability corresponds to a Hopf instability. The key difference between these two types of bifurcations is that the former gives rise to two stable solutions, while the latter leads to periodic solutions (limit cycles). Accordingly, in the superradiant phase the cavity field is static (in the frame of the pump field), while it oscillates periodically in the lasing phase.[6]

See also


References

  1. ↑ 1.0 1.1 1.2 1.3 Hepp, Klaus; Lieb, Elliott H (1973). "On the superradiant phase transition for molecules in a quantized radiation field: the dicke maser model". Annals of Physics 76 (2): 360–404. doi:10.1016/0003-4916(73)90039-0. ISSN 0003-4916. Bibcode: 1973AnPhy..76..360H. 
  2. ↑ 2.0 2.1 2.2 Dicke, R. H. (1954). "Coherence in Spontaneous Radiation Processes". Physical Review 93 (1): 99–110. doi:10.1103/PhysRev.93.99. ISSN 0031-899X. Bibcode: 1954PhRv...93...99D. 
  3. ↑ Note that the spin operators are often represented by Pauli matrices [math]\displaystyle{ \tilde\sigma^\alpha }[/math], through the relation [math]\displaystyle{ \sigma^\alpha=\hbar\tilde\sigma^\alpha/2 }[/math]. In some References, the Hamiltonian of the Dicke model is represented in terms of Pauli matrices, rather than spin operators.
  4. ↑ Larson, Jonas; Irish, Elinor K (2017). "Some remarks on 'superradiant' phase transitions in light-matter systems". Journal of Physics A: Mathematical and Theoretical 50 (17): 174002. doi:10.1088/1751-8121/aa65dc. ISSN 1751-8113. Bibcode: 2017JPhA...50q4002L. 
  5. ↑ See Garraway, B. M. (2011). "The Dicke model in quantum optics: Dicke model revisited". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 369 (1939): 1137–1155. doi:10.1098/rsta.2010.0333. ISSN 1364-503X. PMID 21320910. Bibcode: 2011RSPTA.369.1137G.  and references therein.
  6. ↑ 6.0 6.1 6.2 6.3 See Kirton, Peter; Roses, Mor M.; Keeling, Jonathan; Dalla Torre, Emanuele G. (2018). "Introduction to the Dicke Model: From Equilibrium to Nonequilibrium, and Vice Versa". Advanced Quantum Technologies 2 (1–2): 1800043. doi:10.1002/qute.201800043. ISSN 2511-9044.  and references therein.
  7. ↑ de Aguiar, M.A.M; Furuya, K; Lewenkopf, C.H; Nemes, M.C (1992). "Chaos in a spin-boson system: Classical analysis" (in en). Annals of Physics 216 (2): 291–312. doi:10.1016/0003-4916(92)90178-O. Bibcode: 1992AnPhy.216..291D. https://linkinghub.elsevier.com/retrieve/pii/000349169290178O. 
  8. ↑ 8.0 8.1 Bastarrachea-Magnani, Miguel Angel; López-del-Carpio, Baldemar; Lerma-Hernández, Sergio; Hirsch, Jorge G (2015). "Chaos in the Dicke model: quantum and semiclassical analysis" (in en). Physica Scripta 90 (6): 068015. doi:10.1088/0031-8949/90/6/068015. ISSN 0031-8949. Bibcode: 2015PhyS...90f8015B. https://doi.org/10.1088/0031-8949/90/6/068015. 
  9. ↑ Emary, Clive; Brandes, Tobias (2003). "Quantum Chaos Triggered by Precursors of a Quantum Phase Transition: The Dicke Model". Physical Review Letters 90 (4): 044101. doi:10.1103/PhysRevLett.90.044101. PMID 12570425. Bibcode: 2003PhRvL..90d4101E. https://link.aps.org/doi/10.1103/PhysRevLett.90.044101. 
  10. ↑ Chávez-Carlos, Jorge; Bastarrachea-Magnani, Miguel Angel; Lerma-Hernández, Sergio; Hirsch, Jorge G. (2016). "Classical chaos in atom-field systems". Physical Review E 94 (2): 022209. doi:10.1103/PhysRevE.94.022209. PMID 27627300. Bibcode: 2016PhRvE..94b2209C. https://link.aps.org/doi/10.1103/PhysRevE.94.022209. 
  11. ↑ Chávez-Carlos, Jorge; López-del-Carpio, Baldemar; Bastarrachea-Magnani, Miguel Angel; Stránský, Pavel; Lerma-Hernández, Sergio; Santos, Lea F.; Hirsch, Jorge G. (2019). "Quantum and Classical Lyapunov Exponents in Atom-Field Interaction Systems". Physical Review Letters 122 (2): 024101. doi:10.1103/PhysRevLett.122.024101. PMID 30720302. Bibcode: 2019PhRvL.122b4101C. 
  12. ↑ Pilatowsky-Cameo, Saúl; Chávez-Carlos, Jorge; Bastarrachea-Magnani, Miguel A.; Stránský, Pavel; Lerma-Hernández, Sergio; Santos, Lea F.; Hirsch, Jorge G. (2020). "Positive quantum Lyapunov exponents in experimental systems with a regular classical limit". Physical Review E 101 (1): 010202. doi:10.1103/PhysRevE.101.010202. PMID 32069677. Bibcode: 2020PhRvE.101a0202P. https://link.aps.org/doi/10.1103/PhysRevE.101.010202. 
  13. ↑ Lerma-Hernández, S.; Villaseñor, D.; Bastarrachea-Magnani, M. A.; Torres-Herrera, E. J.; Santos, L. F.; Hirsch, J. G. (2019). "Dynamical signatures of quantum chaos and relaxation time scales in a spin-boson system". Physical Review E 100 (1): 012218. doi:10.1103/PhysRevE.100.012218. PMID 31499773. Bibcode: 2019PhRvE.100a2218L. 
  14. ↑ Villaseñor, David; Pilatowsky-Cameo, Saúl; Bastarrachea-Magnani, Miguel Angel; Lerma-Hernández, Sergio; Santos, Lea F.; Hirsch, Jorge G. (2020). "Quantum vs classical dynamics in a spin-boson system: manifestations of spectral correlations and scarring" (in en). New Journal of Physics 22 (6): 063036. doi:10.1088/1367-2630/ab8ef8. ISSN 1367-2630. Bibcode: 2020NJPh...22f3036V. 
  15. ↑ Aguiar, M. A. M. de; Furuya, K; Lewenkopf, C. H; Nemes, M. C (1991). "Particle-Spin Coupling in a Chaotic System: Localization-Delocalization in the Husimi Distributions" (in en). Europhysics Letters (EPL) 15 (2): 125–131. doi:10.1209/0295-5075/15/2/003. ISSN 0295-5075. Bibcode: 1991EL.....15..125D. https://doi.org/10.1209/0295-5075/15/2/003. 
  16. ↑ Pilatowsky-Cameo, Saúl; Villaseñor, David; Bastarrachea-Magnani, Miguel A; Lerma, Sergio; Santos, Lea F; Hirsch, Jorge G (2021). "Quantum scarring in a spin-boson system: fundamental families of periodic orbits" (in en). New Journal of Physics 23 (3): 033045. doi:10.1088/1367-2630/abd2e6. ISSN 1367-2630. Bibcode: 2021NJPh...23c3045P. 
  17. ↑ Scully, Marlan O.; Zubairy, M. Suhail (1997). Quantum Optics. Cambridge University Press. doi:10.1017/CBO9780511813993. ISBN 9780521435956. 
  18. ↑ Gross, M.; Haroche, S. (1982). "Superradiance: An essay on the theory of collective spontaneous emission". Physics Reports 93 (5): 301–396. doi:10.1016/0370-1573(82)90102-8. ISSN 0370-1573. Bibcode: 1982PhR....93..301G. 
  19. ↑ Frisk Kockum, Anton; Miranowicz, Adam; De Liberato, Simone; Savasta, Salvatore; Nori, Franco (2019). "Ultrastrong coupling between light and matter". Nature Reviews Physics 1 (1): 19–40. doi:10.1038/s42254-018-0006-2. ISSN 2522-5820. Bibcode: 2019NatRP...1...19F. 
  20. ↑ Dimer, F.; Estienne, B.; Parkins, A. S.; Carmichael, H. J. (2007). "Proposed realization of the Dicke-model quantum phase transition in an optical cavity QED system". Physical Review A 75 (1): 013804. doi:10.1103/PhysRevA.75.013804. ISSN 1050-2947. Bibcode: 2007PhRvA..75a3804D. 
  21. ↑ Nagy, D.; Kónya, G.; Szirmai, G.; Domokos, P. (2010). "Dicke-Model Phase Transition in the Quantum Motion of a Bose-Einstein Condensate in an Optical Cavity". Physical Review Letters 104 (13): 130401. doi:10.1103/PhysRevLett.104.130401. ISSN 0031-9007. PMID 20481867. Bibcode: 2010PhRvL.104m0401N. 
  22. ↑ 22.0 22.1 Baumann, Kristian; Guerlin, Christine; Brennecke, Ferdinand; Esslinger, Tilman (2010). "Dicke quantum phase transition with a superfluid gas in an optical cavity". Nature 464 (7293): 1301–1306. doi:10.1038/nature09009. ISSN 0028-0836. PMID 20428162. Bibcode: 2010Natur.464.1301B. 
  23. ↑ Black, Adam T.; Chan, Hilton W.; Vuletić, Vladan (2003). "Observation of Collective Friction Forces due to Spatial Self-Organization of Atoms: From Rayleigh to Bragg Scattering". Physical Review Letters 91 (20): 203001. doi:10.1103/PhysRevLett.91.203001. ISSN 0031-9007. PMID 14683358. Bibcode: 2003PhRvL..91t3001B. 
  24. ↑ Klinder, Jens; Keßler, Hans; Wolke, Matthias; Mathey, Ludwig; Hemmerich, Andreas (2015). "Dynamical phase transition in the open Dicke model". Proceedings of the National Academy of Sciences 112 (11): 3290–3295. doi:10.1073/pnas.1417132112. ISSN 0027-8424. PMID 25733892. Bibcode: 2015PNAS..112.3290K. 
  25. ↑ Ritsch, Helmut; Domokos, Peter; Brennecke, Ferdinand; Esslinger, Tilman (2013). "Cold atoms in cavity-generated dynamical optical potentials". Reviews of Modern Physics 85 (2): 553–601. doi:10.1103/RevModPhys.85.553. ISSN 0034-6861. Bibcode: 2013RvMP...85..553R. 
  26. ↑ Mivehvar, Farokh; Piazza, Francesco; Donner, Tobias; Ritsch, Helmut (2 January 2021). "Cavity QED with quantum gases: new paradigms in many-body physics". Advances in Physics 70 (1): 1–153. doi:10.1080/00018732.2021.1969727. ISSN 0001-8732. Bibcode: 2021AdPhy..70....1M. https://www.tandfonline.com/doi/abs/10.1080/00018732.2021.1969727. 
  27. ↑ Zhiqiang, Zhang; Lee, Chern Hui; Kumar, Ravi; Arnold, K. J.; Masson, Stuart J.; Parkins, A. S.; Barrett, M. D. (2017). "Nonequilibrium phase transition in a spin-1 Dicke model". Optica 4 (4): 424. doi:10.1364/OPTICA.4.000424. ISSN 2334-2536. Bibcode: 2017Optic...4..424Z. 
  28. ↑ 28.0 28.1 Zhang, Zhiqiang; Lee, Chern Hui; Kumar, Ravi; Arnold, K. J.; Masson, Stuart J.; Grimsmo, A. L.; Parkins, A. S.; Barrett, M. D. (2018). "Dicke-model simulation via cavity-assisted Raman transitions". Physical Review A 97 (4): 043858. doi:10.1103/PhysRevA.97.043858. ISSN 2469-9926. Bibcode: 2018PhRvA..97d3858Z. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Dicke_model&oldid=3276591"