Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable—that is, a matrix in which some or all elements are random variables. Many important properties of physical systems can be represented mathematically as matrix problems. For example, the thermal conductivity of a lattice can be computed from the dynamical matrix of the particle-particle interactions within the lattice.
Applications
Engineering
Random matrix theory can be applied to the electrical and communications engineering research efforts to study, model and develop Massive Multiple-Input Multiple-Output (MIMO) radio systems.
Physics
In nuclear physics, random matrices were introduced by Eugene Wigner to model the nuclei of heavy atoms.[1] Wigner postulated that the spacings between the lines in the spectrum of a heavy atom nucleus should resemble the spacings between the eigenvalues of a random matrix, and should depend only on the symmetry class of the underlying evolution.[2] In solid-state physics, random matrices model the behaviour of large disordered Hamiltonians in the mean-field approximation.
In quantum chaos, the Bohigas–Giannoni–Schmit (BGS) conjecture asserts that the spectral statistics of quantum systems whose classical counterparts exhibit chaotic behaviour are described by random matrix theory.[3]
In quantum optics, transformations described by random unitary matrices are crucial for demonstrating the advantage of quantum over classical computation (see, e.g., the boson sampling model).[4] Moreover, such random unitary transformations can be directly implemented in an optical circuit, by mapping their parameters to optical circuit components (that is beam splitters and phase shifters).[5]
Random matrix theory has also found applications to the chiral Dirac operator in quantum chromodynamics,[6] quantum gravity in two dimensions,[7] mesoscopic physics,[8] spin-transfer torque,[9] the fractional quantum Hall effect,[10] Anderson localization,[11] quantum dots,[12] and superconductors[13]
Mathematical statistics and numerical analysis
In multivariate statistics, random matrices were introduced by John Wishart, who sought to estimate covariance matrices of large samples.[14] Chernoff-, Bernstein-, and Hoeffding-type inequalities can typically be strengthened when applied to the maximal eigenvalue (i.e. the eigenvalue of largest magnitude) of a finite sum of random Hermitian matrices.[15] Random matrix theory is used to study the spectral properties of random matrices—such as sample covariance matrices—which is of particular interest in high-dimensional statistics. Random matrix theory also saw applications in neuronal networks[16] and deep learning, with recent work utilizing random matrices to show that hyper-parameter tunings can be cheaply transferred between large neural networks without the need for re-training.[17]
In numerical analysis, random matrices have been used since the work of John von Neumann and Herman Goldstine[18] to describe computation errors in operations such as matrix multiplication. Although random entries are traditional "generic" inputs to an algorithm, the concentration of measure associated with random matrix distributions implies that random matrices will not test large portions of an algorithm's input space.[19]
Number theory
In number theory, the distribution of zeros of the Riemann zeta function (and other L-functions) is modeled by the distribution of eigenvalues of certain random matrices.[20] The connection was first discovered by Hugh Montgomery and Freeman Dyson. It is connected to the Hilbert–Pólya conjecture.
Free probability
The relation of free probability with random matrices[21] is a key reason for the wide use of free probability in other subjects. Voiculescu introduced the concept of freeness around 1983 in an operator algebraic context; at the beginning there was no relation at all with random matrices. This connection was only revealed later in 1991 by Voiculescu;[22] he was motivated by the fact that the limit distribution which he found in his free central limit theorem had appeared before in Wigner's semi-circle law in the random matrix context.
Theoretical neuroscience
In the field of theoretical neuroscience, random matrices are increasingly used to model the network of synaptic connections between neurons in the brain. Dynamical models of neuronal networks with random connectivity matrix were shown to exhibit a phase transition to chaos[23] when the variance of the synaptic weights crosses a critical value, at the limit of infinite system size. Results on random matrices have also shown that the dynamics of random-matrix models are insensitive to mean connection strength. Instead, the stability of fluctuations depends on connection strength variation[24][25] and time to synchrony depends on network topology.[26][27]
Optimal control
In optimal control theory, the evolution of n state variables through time depends at any time on their own values and on the values of k control variables. With linear evolution, matrices of coefficients appear in the state equation (equation of evolution). In some problems the values of the parameters in these matrices are not known with certainty, in which case there are random matrices in the state equation and the problem is known as one of stochastic control.[28]:ch. 13[29][30] A key result in the case of linear-quadratic control with stochastic matrices is that the certainty equivalence principle does not apply: while in the absence of multiplier uncertainty (that is, with only additive uncertainty) the optimal policy with a quadratic loss function coincides with what would be decided if the uncertainty were ignored, the optimal policy may differ if the state equation contains random coefficients.
Computational mechanics
In computational mechanics, epistemic uncertainties underlying the lack of knowledge about the physics of the modeled system give rise to mathematical operators associated with the computational model, which are deficient in a certain sense. Such operators lack certain properties linked to unmodeled physics. When such operators are discretized to perform computational simulations, their accuracy is limited by the missing physics. To compensate for this deficiency of the mathematical operator, it is not enough to make the model parameters random, it is necessary to consider a mathematical operator that is random and can thus generate families of computational models in the hope that one of these captures the missing physics. Random matrices have been used in this sense,[31][32] with applications in vibroacoustics, wave propagations, materials science, fluid mechanics, heat transfer, etc.
Gaussian ensembles
The most-commonly studied random matrix distributions are the Gaussian ensembles: GOE, GUE and GSE. They are often denoted by their Dyson index, β = 1 for GOE, β = 2 for GUE, and β = 4 for GSE. This index counts the number of real components per matrix element.
Definitions
The Gaussian unitary ensemble [math]\displaystyle{ \text{GUE}(n) }[/math] is described by the Gaussian measure with density [math]\displaystyle{ \frac{1}{Z_{\text{GUE}(n)}} e^{- \frac{n}{2} \mathrm{tr} H^2} }[/math] on the space of [math]\displaystyle{ n \times n }[/math] Hermitian matrices [math]\displaystyle{ H = (H_{ij})_{i,j=1}^n }[/math]. Here [math]\displaystyle{ Z_{\text{GUE}(n)} = 2^{n/2} \left(\frac{\pi}{n}\right)^{\frac{1}{2}n^2} }[/math] is a normalization constant, chosen so that the integral of the density is equal to one. The term unitary refers to the fact that the distribution is invariant under unitary conjugation. The Gaussian unitary ensemble models Hamiltonians lacking time-reversal symmetry.
The Gaussian orthogonal ensemble [math]\displaystyle{ \text{GOE}(n) }[/math] is described by the Gaussian measure with density [math]\displaystyle{ \frac{1}{Z_{\text{GOE}(n)}} e^{- \frac{n}{4} \mathrm{tr} H^2} }[/math] on the space of n × n real symmetric matrices H = (Hij)ni,j=1. Its distribution is invariant under orthogonal conjugation, and it models Hamiltonians with time-reversal symmetry. Equivalently, it is generated by [math]\displaystyle{ H = (G+G^T)/\sqrt{2n} }[/math], where [math]\displaystyle{ G }[/math] is an [math]\displaystyle{ n\times n }[/math] matrix with IID samples from the standard normal distribution.
The Gaussian symplectic ensemble [math]\displaystyle{ \text{GSE}(n) }[/math] is described by the Gaussian measure with density [math]\displaystyle{ \frac{1}{Z_{\text{GSE}(n)}} e^{- n \mathrm{tr} H^2} }[/math] on the space of n × n Hermitian quaternionic matrices, e.g. symmetric square matrices composed of quaternions, H = (Hij)ni,j=1. Its distribution is invariant under conjugation by the symplectic group, and it models Hamiltonians with time-reversal symmetry but no rotational symmetry.
Point correlation functions
The ensembles as defined here have Gaussian distributed matrix elements with mean ⟨Hij⟩ = 0, and two-point correlations given by [math]\displaystyle{ \langle H_{ij} H_{mn}^* \rangle = \langle H_{ij} H_{nm} \rangle = \frac{1}{n} \delta_{im} \delta_{jn} + \frac{2 - \beta}{n \beta}\delta_{in}\delta_{jm} , }[/math] from which all higher correlations follow by Isserlis' theorem.
Moment generating functions
The moment generating function for the GOE is[math]\displaystyle{ E[e^{tr(VH)}] = e^{\frac{1}{4N}\|V + V^T\|_F^2} }[/math]where [math]\displaystyle{ \|\cdot \|_F }[/math] is the Frobenius norm.
Spectral density
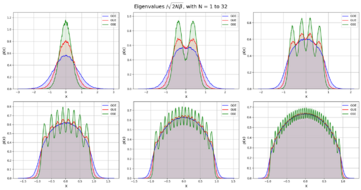
The joint probability density for the eigenvalues λ1, λ2, ..., λn of GUE/GOE/GSE is given by
[math]\displaystyle{ \frac{1}{Z_{\beta, n}} \prod_{k=1}^n e^{-\frac{\beta}{4}\lambda_k^2}\prod_{i\lt j}\left|\lambda_j-\lambda_i\right|^\beta~, }[/math] |
|
() |
where Zβ,n is a normalization constant which can be explicitly computed, see Selberg integral. In the case of GUE (β = 2), the formula (1) describes a determinantal point process. Eigenvalues repel as the joint probability density has a zero (of [math]\displaystyle{ \beta }[/math]th order) for coinciding eigenvalues [math]\displaystyle{ \lambda_j = \lambda_i }[/math].
The distribution of the largest eigenvalue for GOE, and GUE, are explicitly solvable.[33] They converge to the Tracy–Widom distribution after shifting and scaling appropriately.
Convergence to Wigner semicircular distribution
The spectrum, divided by [math]\displaystyle{ \sqrt{N\sigma^2} }[/math], converges in distribution to the semicircular distribution on the interval [math]\displaystyle{ [-2, +2] }[/math]: [math]\displaystyle{ \rho(x) = \frac{1}{2 \pi}\sqrt{4-x^2} }[/math]. Here [math]\displaystyle{ \sigma^2 }[/math] is the variance of off-diagonal entries.
Distribution of level spacings
From the ordered sequence of eigenvalues [math]\displaystyle{ \lambda_1 \lt \ldots \lt \lambda_n \lt \lambda_{n+1} \lt \ldots }[/math], one defines the normalized spacings [math]\displaystyle{ s = (\lambda_{n+1} - \lambda_n)/\langle s \rangle }[/math], where [math]\displaystyle{ \langle s \rangle =\langle \lambda_{n+1} - \lambda_n \rangle }[/math] is the mean spacing. The probability distribution of spacings is approximately given by, [math]\displaystyle{ p_1(s) = \frac{\pi}{2}s\, e^{-\frac{\pi}{4} s^2} }[/math] for the orthogonal ensemble GOE [math]\displaystyle{ \beta=1 }[/math], [math]\displaystyle{ p_2(s) = \frac{32}{\pi^2}s^2 \mathrm{e}^{-\frac{4}{\pi} s^2} }[/math] for the unitary ensemble GUE [math]\displaystyle{ \beta=2 }[/math], and [math]\displaystyle{ p_4(s) = \frac{2^{18}}{3^6\pi^3}s^4 e^{-\frac{64}{9\pi} s^2} }[/math] for the symplectic ensemble GSE [math]\displaystyle{ \beta = 4 }[/math].
The numerical constants are such that [math]\displaystyle{ p_\beta(s) }[/math] is normalized: [math]\displaystyle{ \int_0^\infty ds\,p_\beta(s) = 1 }[/math] and the mean spacing is, [math]\displaystyle{ \int_0^\infty ds\, s\, p_\beta(s) = 1, }[/math] for [math]\displaystyle{ \beta = 1,2,4 }[/math].
Generalizations
Wigner matrices are random Hermitian matrices [math]\displaystyle{ H_n = (H_n(i,j))_{i,j=1}^n }[/math] such that the entries [math]\displaystyle{ \left\{ H_n(i, j)~, \, 1 \leq i \leq j \leq n \right\} }[/math] above the main diagonal are independent random variables with zero mean and have identical second moments.
Invariant matrix ensembles are random Hermitian matrices with density on the space of real symmetric/Hermitian/quaternionic Hermitian matrices, which is of the form [math]\displaystyle{ \frac{1}{Z_n} e^{- n V(\mathrm{tr}(H))}~, }[/math] where the function V is called the potential.
The Gaussian ensembles are the only common special cases of these two classes of random matrices. This is a consequence of a theorem by Porter and Rosenzweig.[34][35]
Spectral theory of random matrices
The spectral theory of random matrices studies the distribution of the eigenvalues as the size of the matrix goes to infinity.
Global regime
In the global regime, one is interested in the distribution of linear statistics of the form [math]\displaystyle{ N_{f, H} = n^{-1} \text{tr} f(H) }[/math].
Empirical spectral measure
The empirical spectral measure μH of H is defined by [math]\displaystyle{ \mu_{H}(A) = \frac{1}{n} \, \# \left\{ \text{eigenvalues of }H\text{ in }A \right\} = N_{1_A, H}, \quad A \subset \mathbb{R}. }[/math]
Usually, the limit of [math]\displaystyle{ \mu_{H} }[/math] is a deterministic measure; this is a particular case of self-averaging. The cumulative distribution function of the limiting measure is called the integrated density of states and is denoted N(λ). If the integrated density of states is differentiable, its derivative is called the density of states and is denoted ρ(λ).
The limit of the empirical spectral measure for Wigner matrices was described by Eugene Wigner; see Wigner semicircle distribution and Wigner surmise. As far as sample covariance matrices are concerned, a theory was developed by Marčenko and Pastur.[36][37]
The limit of the empirical spectral measure of invariant matrix ensembles is described by a certain integral equation which arises from potential theory.[38]
Fluctuations
For the linear statistics Nf,H = n−1 Σ f(λj), one is also interested in the fluctuations about ∫ f(λ) dN(λ). For many classes of random matrices, a central limit theorem of the form [math]\displaystyle{ \frac{N_{f,H} - \int f(\lambda) \, dN(\lambda)}{\sigma_{f, n}} \overset{D}{\longrightarrow} N(0, 1) }[/math] is known.[39][40]
The variational problem for the unitary ensembles
Consider the measure
- [math]\displaystyle{ \mathrm{d}\mu_N(\mu)=\frac{1}{\widetilde{Z}_N}e^{-H_N(\lambda)}\mathrm{d}\lambda,\qquad H_N(\lambda)=-\sum\limits_{j\neq k}\ln|\lambda_j-\lambda_k|+N\sum\limits_{j=1}^N Q(\lambda_j), }[/math]
where [math]\displaystyle{ Q(M) }[/math] is the potential of the ensemble and let [math]\displaystyle{ \nu }[/math] be the empirical spectral measure.
We can rewrite [math]\displaystyle{ H_N(\lambda) }[/math] with [math]\displaystyle{ \nu }[/math] as
- [math]\displaystyle{ H_N(\lambda)=N^2\left[-\int\int_{x\neq y}\ln |x-y|\mathrm{d}\nu(x)\mathrm{d}\nu(y)+\int Q(x)\mathrm{d}\nu(x)\right], }[/math]
the probability measure is now of the form
- [math]\displaystyle{ \mathrm{d}\mu_N(\mu)=\frac{1}{\widetilde{Z}_N}e^{-N^2 I_Q(\nu)}\mathrm{d}\lambda, }[/math]
where [math]\displaystyle{ I_Q(\nu) }[/math] is the above functional inside the squared brackets.
Let now
- [math]\displaystyle{ M_1(\mathbb{R})=\left\{\nu:\nu\geq 0,\ \int_{\mathbb{R}}\mathrm{d}\nu = 1\right\} }[/math]
be the space of one-dimensional probability measures and consider the minimizer
- [math]\displaystyle{ E_Q=\inf\limits_{\nu \in M_1(\mathbb{R})}-\int\int_{x\neq y} \ln |x-y|\mathrm{d}\nu(x)\mathrm{d}\nu(y)+\int Q(x)\mathrm{d}\nu(x). }[/math]
For [math]\displaystyle{ E_Q }[/math] there exists a unique equilibrium measure [math]\displaystyle{ \nu_{Q} }[/math] through the Euler-Lagrange variational conditions for some real constant [math]\displaystyle{ l }[/math]
- [math]\displaystyle{ 2\int_\mathbb{R}\log |x-y|\mathrm{d}\nu(y)-Q(x)=l,\quad x\in J }[/math]
- [math]\displaystyle{ 2\int_\mathbb{R}\log |x-y|\mathrm{d}\nu(y)-Q(x)\leq l,\quad x\in \mathbb{R}\setminus J }[/math]
where [math]\displaystyle{ J=\bigcup\limits_{j=1}^q[a_j,b_j] }[/math] is the support of the measure and
- [math]\displaystyle{ q=-\left(\frac{Q'(x)}{2}\right)^2+\int \frac{Q'(x)-Q'(y)}{x-y}\mathrm{d}\nu_{Q}(y) }[/math].
The equilibrium measure [math]\displaystyle{ \nu_{Q} }[/math] has the following Radon–Nikodym density
- [math]\displaystyle{ \frac{\mathrm{d}\nu_{Q}(x)}{\mathrm{d}x}=\frac{1}{\pi}\sqrt{q(x)}. }[/math][41]
Local regime
In the local regime, one is interested in the spacings between eigenvalues, and, more generally, in the joint distribution of eigenvalues in an interval of length of order 1/n. One distinguishes between bulk statistics, pertaining to intervals inside the support of the limiting spectral measure, and edge statistics, pertaining to intervals near the boundary of the support.
Bulk statistics
Formally, fix [math]\displaystyle{ \lambda_0 }[/math] in the interior of the support of [math]\displaystyle{ N(\lambda) }[/math]. Then consider the point process [math]\displaystyle{ \Xi(\lambda_0) = \sum_j \delta\Big({\cdot} - n \rho(\lambda_0) (\lambda_j - \lambda_0) \Big)~, }[/math] where [math]\displaystyle{ \lambda_j }[/math] are the eigenvalues of the random matrix.
The point process [math]\displaystyle{ \Xi(\lambda_0) }[/math] captures the statistical properties of eigenvalues in the vicinity of [math]\displaystyle{ \lambda_0 }[/math]. For the Gaussian ensembles, the limit of [math]\displaystyle{ \Xi(\lambda_0) }[/math] is known;[2] thus, for GUE it is a determinantal point process with the kernel [math]\displaystyle{ K(x, y) = \frac{\sin \pi(x-y)}{\pi(x-y)} }[/math] (the sine kernel).
The universality principle postulates that the limit of [math]\displaystyle{ \Xi(\lambda_0) }[/math] as [math]\displaystyle{ n \to \infty }[/math] should depend only on the symmetry class of the random matrix (and neither on the specific model of random matrices nor on [math]\displaystyle{ \lambda_0 }[/math]). Rigorous proofs of universality are known for invariant matrix ensembles[42][43] and Wigner matrices.[44][45]
Edge statistics
Local laws
[46] The typical statement of the Wigner semicircular law is equivalent to the following statement: For each fixed interval [math]\displaystyle{ [\lambda_0 - \Delta \lambda, \lambda_0 + \Delta \lambda] }[/math] centered at a point [math]\displaystyle{ \lambda_0 }[/math], as [math]\displaystyle{ N }[/math], the number of dimensions of the gaussian ensemble increases, the proportion of the eigenvalues falling within the interval converges to [math]\displaystyle{ \int_{[\lambda_0 - \Delta \lambda, \lambda_0 + \Delta \lambda]} \rho(t) dt }[/math], where [math]\displaystyle{ \rho(t) }[/math] is the density of the semicircular distribution.
If [math]\displaystyle{ \Delta \lambda }[/math] can be allowed to decrease as [math]\displaystyle{ N }[/math] increases, then we obtain strictly stronger theorems, named "local laws".
Correlation functions
The joint probability density of the eigenvalues of [math]\displaystyle{ n\times n }[/math] random Hermitian matrices [math]\displaystyle{ M \in \mathbf{H}^{n \times n} }[/math], with partition functions of the form [math]\displaystyle{ Z_n = \int_{M \in \mathbf{H}^{n \times n}} d\mu_0(M)e^{\text{tr}(V(M))} }[/math] where [math]\displaystyle{ V(x):=\sum_{j=1}^\infty v_j x^j }[/math] and [math]\displaystyle{ d\mu_0(M) }[/math] is the standard Lebesgue measure on the space [math]\displaystyle{ \mathbf{H}^{n \times n} }[/math] of Hermitian [math]\displaystyle{ n \times n }[/math] matrices, is given by [math]\displaystyle{ p_{n,V}(x_1,\dots, x_n) = \frac{1}{Z_{n,V}}\prod_{i\lt j} (x_i-x_j)^2 e^{-\sum_i V(x_i)}. }[/math] The [math]\displaystyle{ k }[/math]-point correlation functions (or marginal distributions) are defined as [math]\displaystyle{ R^{(k)}_{n,V}(x_1,\dots,x_k) = \frac{n!}{(n-k)!} \int_{\mathbf{R}}dx_{k+1} \cdots \int_{\R} dx_{n} \, p_{n,V}(x_1,x_2,\dots,x_n), }[/math] which are skew symmetric functions of their variables. In particular, the one-point correlation function, or density of states, is [math]\displaystyle{ R^{(1)}_{n,V}(x_1) = n\int_{\R}dx_{2} \cdots \int_{\mathbf{R}} dx_{n} \, p_{n,V}(x_1,x_2,\dots,x_n). }[/math] Its integral over a Borel set [math]\displaystyle{ B \subset \mathbf{R} }[/math] gives the expected number of eigenvalues contained in [math]\displaystyle{ B }[/math]: [math]\displaystyle{ \int_{B} R^{(1)}_{n,V}(x)dx = \mathbf{E}\left(\#\{\text{eigenvalues in }B\}\right). }[/math]
The following result expresses these correlation functions as determinants of the matrices formed from evaluating the appropriate integral kernel at the pairs [math]\displaystyle{ (x_i, x_j) }[/math] of points appearing within the correlator.
Theorem [Dyson-Mehta] For any [math]\displaystyle{ k }[/math], [math]\displaystyle{ 1\leq k \leq n }[/math] the [math]\displaystyle{ k }[/math]-point correlation function [math]\displaystyle{ R^{(k)}_{n,V} }[/math] can be written as a determinant [math]\displaystyle{ R^{(k)}_{n,V}(x_1,x_2,\dots,x_k) = \det_{1\leq i,j \leq k}\left(K_{n,V}(x_i,x_j)\right), }[/math] where [math]\displaystyle{ K_{n,V}(x,y) }[/math] is the [math]\displaystyle{ n }[/math]th Christoffel-Darboux kernel [math]\displaystyle{ K_{n,V}(x,y) := \sum_{k=0}^{n-1}\psi_k(x)\psi_k(y), }[/math] associated to [math]\displaystyle{ V }[/math], written in terms of the quasipolynomials [math]\displaystyle{ \psi_k(x) = {1\over \sqrt{h_k}}\, p_k(z)\, e^{- V(z) / 2} , }[/math] where [math]\displaystyle{ \{p_k(x)\}_{k\in \mathbf{N}} }[/math] is a complete sequence of monic polynomials, of the degrees indicated, satisfying the orthogonilty conditions [math]\displaystyle{ \int_{\mathbf{R}} \psi_j(x) \psi_k(x) dx = \delta_{jk}. }[/math]
Other classes of random matrices
Wishart matrices
Wishart matrices are n × n random matrices of the form H = X X*, where X is an n × m random matrix (m ≥ n) with independent entries, and X* is its conjugate transpose. In the important special case considered by Wishart, the entries of X are identically distributed Gaussian random variables (either real or complex).
The limit of the empirical spectral measure of Wishart matrices was found[36] by Vladimir Marchenko and Leonid Pastur.
Random unitary matrices
Non-Hermitian random matrices
Selected bibliography
Books
- Mehta, M.L. (2004). Random Matrices. Amsterdam: Elsevier/Academic Press. ISBN 0-12-088409-7.
- Anderson, G.W.; Guionnet, A.; Zeitouni, O. (2010). An introduction to random matrices.. Cambridge: Cambridge University Press. ISBN 978-0-521-19452-5.
- Akemann, G.; Baik, J.; Di Francesco, P. (2011). The Oxford Handbook of Random Matrix Theory. Oxford: Oxford University Press. ISBN 978-0-19-957400-1.
Survey articles
- Edelman, A.; Rao, N.R (2005). "Random matrix theory". Acta Numerica 14: 233–297. doi:10.1017/S0962492904000236. Bibcode: 2005AcNum..14..233E.
- Pastur, L.A. (1973). "Spectra of random self-adjoint operators". Russ. Math. Surv. 28 (1): 1–67. doi:10.1070/RM1973v028n01ABEH001396. Bibcode: 1973RuMaS..28....1P.
- Diaconis, Persi (2003). "Patterns in eigenvalues: the 70th Josiah Willard Gibbs lecture". Bulletin of the American Mathematical Society. New Series 40 (2): 155–178. doi:10.1090/S0273-0979-03-00975-3.
- Diaconis, Persi (2005). "What is ... a random matrix?". Notices of the American Mathematical Society 52 (11): 1348–1349. ISSN 0002-9920. https://www.ams.org/notices/200511/.
- Eynard, Bertrand; Kimura, Taro; Ribault, Sylvain (2015-10-15). "Random matrices". arXiv:1510.04430v2 [math-ph].
Historic works
- Wigner, E. (1955). "Characteristic vectors of bordered matrices with infinite dimensions". Annals of Mathematics 62 (3): 548–564. doi:10.2307/1970079.
- Wishart, J. (1928). "Generalized product moment distribution in samples". Biometrika 20A (1–2): 32–52. doi:10.1093/biomet/20a.1-2.32.
- von Neumann, J.; Goldstine, H.H. (1947). "Numerical inverting of matrices of high order". Bull. Amer. Math. Soc. 53 (11): 1021–1099. doi:10.1090/S0002-9904-1947-08909-6.
References
- ↑ Wigner 1955
- ↑ 2.0 2.1 Mehta 2004
- ↑ Bohigas, O.; Giannoni, M.J.; Schmit, Schmit (1984). "Characterization of Chaotic Quantum Spectra and Universality of Level Fluctuation Laws". Phys. Rev. Lett. 52 (1): 1–4. doi:10.1103/PhysRevLett.52.1. Bibcode: 1984PhRvL..52....1B.
- ↑ Aaronson, Scott; Arkhipov, Alex (2013). "The computational complexity of linear optics". Theory of Computing 9: 143–252. doi:10.4086/toc.2013.v009a004.
- ↑ Russell, Nicholas; Chakhmakhchyan, Levon; O'Brien, Jeremy; Laing, Anthony (2017). "Direct dialling of Haar random unitary matrices". New J. Phys. 19 (3): 033007. doi:10.1088/1367-2630/aa60ed. Bibcode: 2017NJPh...19c3007R.
- ↑ "Random Matrix Theory and Chiral Symmetry in QCD". Annu. Rev. Nucl. Part. Sci. 50: 343–410. 2000. doi:10.1146/annurev.nucl.50.1.343. Bibcode: 2000ARNPS..50..343V.
- ↑ "Horizon in random matrix theory, the Hawking radiation, and flow of cold atoms". Phys. Rev. Lett. 103 (16): 166401. October 2009. doi:10.1103/PhysRevLett.103.166401. PMID 19905710. Bibcode: 2009PhRvL.103p6401F.
- ↑ "Magnetic-field asymmetry of nonlinear mesoscopic transport". Phys. Rev. Lett. 93 (10): 106802. September 2004. doi:10.1103/PhysRevLett.93.106802. PMID 15447435. Bibcode: 2004PhRvL..93j6802S.
- ↑ "Spin torque and waviness in magnetic multilayers: a bridge between Valet-Fert theory and quantum approaches". Phys. Rev. Lett. 103 (6): 066602. August 2009. doi:10.1103/PhysRevLett.103.066602. PMID 19792592. Bibcode: 2009PhRvL.103f6602R.
- ↑ Callaway DJE (April 1991). "Random matrices, fractional statistics, and the quantum Hall effect". Phys. Rev. B 43 (10): 8641–8643. doi:10.1103/PhysRevB.43.8641. PMID 9996505. Bibcode: 1991PhRvB..43.8641C.
- ↑ "Correlated random band matrices: localization-delocalization transitions". Phys. Rev. E 61 (6 Pt A): 6278–86. June 2000. doi:10.1103/PhysRevE.61.6278. PMID 11088301. Bibcode: 2000PhRvE..61.6278J.
- ↑ "Spin-orbit coupling, antilocalization, and parallel magnetic fields in quantum dots". Phys. Rev. Lett. 89 (27): 276803. December 2002. doi:10.1103/PhysRevLett.89.276803. PMID 12513231. Bibcode: 2002PhRvL..89A6803Z.
- ↑ Bahcall SR (December 1996). "Random Matrix Model for Superconductors in a Magnetic Field". Phys. Rev. Lett. 77 (26): 5276–5279. doi:10.1103/PhysRevLett.77.5276. PMID 10062760. Bibcode: 1996PhRvL..77.5276B.
- ↑ Wishart 1928
- ↑ Tropp, J. (2011). "User-Friendly Tail Bounds for Sums of Random Matrices". Foundations of Computational Mathematics 12 (4): 389–434. doi:10.1007/s10208-011-9099-z.
- ↑ Pennington, Jeffrey; Bahri, Yasaman (2017). "Geometry of Neural Network Loss Surfaces via Random Matrix Theory". ICML'17: Proceedings of the 34th International Conference on Machine Learning 70.
- ↑ Yang, Greg (2022). "Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer". arXiv:2203.03466v2 [cs.LG].
- ↑ von Neumann & Goldstine 1947
- ↑ Edelman & Rao 2005
- ↑ Keating, Jon (1993). "The Riemann zeta-function and quantum chaology". Proc. Internat. School of Phys. Enrico Fermi CXIX: 145–185. doi:10.1016/b978-0-444-81588-0.50008-0. ISBN 9780444815880.
- ↑ Mingo, James A.; Speicher, Roland (2017): Free Probability and Random Matrices. Fields Institute Monographs, Vol. 35, Springer, New York
- ↑ Voiculescu, Dan (1991): "Limit laws for random matrices and free products". Inventiones mathematicae 104.1: 201-220
- ↑ Sompolinsky, H.; Crisanti, A.; Sommers, H. (July 1988). "Chaos in Random Neural Networks". Physical Review Letters 61 (3): 259–262. doi:10.1103/PhysRevLett.61.259. PMID 10039285. Bibcode: 1988PhRvL..61..259S.
- ↑ Rajan, Kanaka; Abbott, L. (November 2006). "Eigenvalue Spectra of Random Matrices for Neural Networks". Physical Review Letters 97 (18): 188104. doi:10.1103/PhysRevLett.97.188104. PMID 17155583. Bibcode: 2006PhRvL..97r8104R.
- ↑ Wainrib, Gilles; Touboul, Jonathan (March 2013). "Topological and Dynamical Complexity of Random Neural Networks". Physical Review Letters 110 (11): 118101. doi:10.1103/PhysRevLett.110.118101. PMID 25166580. Bibcode: 2013PhRvL.110k8101W.
- ↑ Timme, Marc; Wolf, Fred; Geisel, Theo (February 2004). "Topological Speed Limits to Network Synchronization". Physical Review Letters 92 (7): 074101. doi:10.1103/PhysRevLett.92.074101. PMID 14995853. Bibcode: 2004PhRvL..92g4101T.
- ↑ Muir, Dylan; Mrsic-Flogel, Thomas (2015). "Eigenspectrum bounds for semirandom matrices with modular and spatial structure for neural networks". Phys. Rev. E 91 (4): 042808. doi:10.1103/PhysRevE.91.042808. PMID 25974548. Bibcode: 2015PhRvE..91d2808M. http://edoc.unibas.ch/41441/1/20160120100936_569f4ed0ddeee.pdf.
- ↑ Chow, Gregory P. (1976). Analysis and Control of Dynamic Economic Systems. New York: Wiley. ISBN 0-471-15616-7.
- ↑ Turnovsky, Stephen (1976). "Optimal stabilization policies for stochastic linear systems: The case of correlated multiplicative and additive disturbances". Review of Economic Studies 43 (1): 191–194. doi:10.2307/2296614.
- ↑ Turnovsky, Stephen (1974). "The stability properties of optimal economic policies". American Economic Review 64 (1): 136–148.
- ↑ Soize, C. (2000-07-01). "A nonparametric model of random uncertainties for reduced matrix models in structural dynamics" (in en). Probabilistic Engineering Mechanics 15 (3): 277–294. doi:10.1016/S0266-8920(99)00028-4. ISSN 0266-8920. https://www.sciencedirect.com/science/article/abs/pii/S0266892099000284.
- ↑ Soize, C. (2005-04-08). "Random matrix theory for modeling uncertainties in computational mechanics" (in en). Computer Methods in Applied Mechanics and Engineering 194 (12–16): 1333–1366. doi:10.1016/j.cma.2004.06.038. ISSN 1879-2138. Bibcode: 2005CMAME.194.1333S. https://hal-upec-upem.archives-ouvertes.fr/hal-00686187/file/publi-2005-CMAME-194_12-16_1333-1366-soize-preprint.pdf.
- ↑ Chiani M (2014). "Distribution of the largest eigenvalue for real Wishart and Gaussian random matrices and a simple approximation for the Tracy-Widom distribution". Journal of Multivariate Analysis 129: 69–81. doi:10.1016/j.jmva.2014.04.002.
- ↑ Porter, C. E.; Rosenzweig, N. (1960-01-01). "STATISTICAL PROPERTIES OF ATOMIC AND NUCLEAR SPECTRA" (in English). Ann. Acad. Sci. Fennicae. Ser. A VI 44. https://www.osti.gov/biblio/4147616.
- ↑ Livan, Giacomo; Novaes, Marcel; Vivo, Pierpaolo (2018), Livan, Giacomo; Novaes, Marcel; Vivo, Pierpaolo, eds., "Classified Material" (in en), Introduction to Random Matrices: Theory and Practice, SpringerBriefs in Mathematical Physics (Cham: Springer International Publishing) 26: pp. 15–21, doi:10.1007/978-3-319-70885-0_3, ISBN 978-3-319-70885-0, https://doi.org/10.1007/978-3-319-70885-0_3, retrieved 2023-05-17
- ↑ 36.0 36.1 .Marčenko, V A; Pastur, L A (1967). "Distribution of eigenvalues for some sets of random matrices". Mathematics of the USSR-Sbornik 1 (4): 457–483. doi:10.1070/SM1967v001n04ABEH001994. Bibcode: 1967SbMat...1..457M.
- ↑ Pastur 1973
- ↑ Pastur, L.; Shcherbina, M. (1995). "On the Statistical Mechanics Approach in the Random Matrix Theory: Integrated Density of States". J. Stat. Phys. 79 (3–4): 585–611. doi:10.1007/BF02184872. Bibcode: 1995JSP....79..585D.
- ↑ Johansson, K. (1998). "On fluctuations of eigenvalues of random Hermitian matrices". Duke Math. J. 91 (1): 151–204. doi:10.1215/S0012-7094-98-09108-6.
- ↑ Pastur, L.A. (2005). "A simple approach to the global regime of Gaussian ensembles of random matrices". Ukrainian Math. J. 57 (6): 936–966. doi:10.1007/s11253-005-0241-4. http://dspace.nbuv.gov.ua/handle/123456789/165749.
- ↑ Harnad, John (15 July 2013). Random Matrices, Random Processes and Integrable Systems. Springer. pp. 263–266. ISBN 978-1461428770.
- ↑ Pastur, L. (1997). "Universality of the local eigenvalue statistics for a class of unitary invariant random matrix ensembles". Journal of Statistical Physics 86 (1–2): 109–147. doi:10.1007/BF02180200. Bibcode: 1997JSP....86..109P. http://purl.umn.edu/2773.
- ↑ Deift, P.; Kriecherbauer, T.; McLaughlin, K.T.-R.; Venakides, S.; Zhou, X. (1997). "Asymptotics for polynomials orthogonal with respect to varying exponential weights". International Mathematics Research Notices 1997 (16): 759–782. doi:10.1155/S1073792897000500.
- ↑ Erdős, L. (2010). "Bulk universality for Wigner matrices". Communications on Pure and Applied Mathematics 63 (7): 895–925.
- ↑ "Random matrices: universality of local eigenvalue statistics up to the edge". Communications in Mathematical Physics 298 (2): 549–572. 2010. doi:10.1007/s00220-010-1044-5. Bibcode: 2010CMaPh.298..549T.
- ↑ Erdős, László; Schlein, Benjamin; Yau, Horng-Tzer (April 2009). "Local Semicircle Law and Complete Delocalization for Wigner Random Matrices" (in en). Communications in Mathematical Physics 287 (2): 641–655. doi:10.1007/s00220-008-0636-9. ISSN 0010-3616. http://link.springer.com/10.1007/s00220-008-0636-9.
External links
- Fyodorov, Y. (2011). "Random matrix theory". Scholarpedia 6 (3): 9886. doi:10.4249/scholarpedia.9886. Bibcode: 2011SchpJ...6.9886F.
- Weisstein, E. W.. "Random Matrix". Wolfram MathWorld. http://mathworld.wolfram.com/RandomMatrix.html.
 |

