Physics:Hong–Ou–Mandel effect

From HandWiki
Revision as of 03:02, 5 February 2024 by Scavis2 (talk | contribs) (change)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Interference effect of two photons


The Hong–Ou–Mandel effect is a two-photon interference effect in quantum optics that was demonstrated in 1987 by three physicists from the University of Rochester: Chung Ki Hong (홍정기), Zheyu Ou (区泽宇), and Leonard Mandel.[1] The effect occurs when two identical single-photons enter a 1:1 beam splitter, one in each input port. When the temporal overlap of the photons on the beam splitter is perfect, the two photons will always exit the beam splitter together in the same output mode, meaning that there is zero chance that they will exit separately with one photon in each of the two outputs giving a coincidence event. The photons have a 50:50 chance of exiting (together) in either output mode. If they become more distinguishable (e.g. because they arrive at different times or with different wavelength), the probability of them each going to a different detector will increase. In this way, the interferometer coincidence signal can accurately measure bandwidth, path lengths, and timing. Since this effect relies on the existence of photons and the second quantization it can not be fully explained by classical optics.

The effect provides one of the underlying physical mechanisms for logic gates in linear optical quantum computing[2] (the other mechanism being the action of measurement).

Quantum-mechanical description

Physical description

When a photon enters a beam splitter, there are two possibilities: it will either be reflected or transmitted. The relative probabilities of transmission and reflection are determined by the reflectivity of the beam splitter. Here, we assume a 1:1 beam splitter, in which a photon has equal probability of being reflected and transmitted.

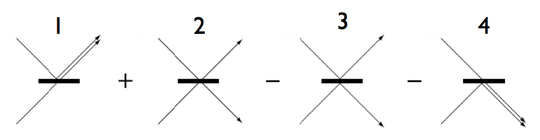
Next, consider two photons, one in each input mode of a 1:1 beam splitter. There are four possibilities regarding how the photons will behave:

  1. The photon coming in from above is reflected and the photon coming in from below is transmitted.
  2. Both photons are transmitted.
  3. Both photons are reflected.
  4. The photon coming in from above is transmitted and the photon coming in from below is reflected.

We assume now that the two photons are identical in their physical properties (i.e., polarization, spatio-temporal mode structure, and frequency).

The four possibilities of two-photon reflection and transmission are added at the amplitude level.

Since the state of the beam splitter does not "record" which of the four possibilities actually happens, Feynman rules dictates that we have to add all four possibilities at the probability amplitude level. In addition, reflection from the bottom side of the beam splitter introduces a relative phase shift of π, corresponding to a factor of −1 in the associated term in the superposition. This sign is required by the reversibility (or unitarity of the quantum evolution) of the beam splitter. Since the two photons are identical, we cannot distinguish between the output states of possibilities 2 and 3, and their relative minus sign ensures that these two terms cancel. This cancelation can be interpreted as destructive interference of the transmission/transmission and reflection/reflection possibilities. If a detector is set up on each of the outputs then coincidences can never be observed, while both photons can appear together in either one of the two detectors with equal probability. A classical prediction of the intensities of the output beams for the same beam splitter and identical coherent input beams would suggest that all of the light should go to one of the outputs (the one with the positive phase).

Mathematical description

Consider two optical input modes a and b that carry annihilation and creation operators [math]\displaystyle{ \hat{a} }[/math], [math]\displaystyle{ \hat{a}^\dagger }[/math], and [math]\displaystyle{ \hat{b} }[/math], [math]\displaystyle{ \hat{b}^\dagger }[/math]. Identical photons in different modes can be described by the Fock states, so, for example [math]\displaystyle{ |0\rangle_a }[/math] corresponds to mode a empty (the vacuum state), and inserting one photon into a corresponds to [math]\displaystyle{ |1\rangle_a=\hat{a}^\dagger|0\rangle_a }[/math], etc. A photon in each input mode is therefore

[math]\displaystyle{ |1, 1\rangle_{ab} = \hat{a}^\dagger \hat{b}^\dagger |0, 0\rangle_{ab}. }[/math]

When the two modes a and b are mixed in a 1:1 beam splitter, they produce output modes c and d. Inserting a photon in a produces a superposition state of the outputs: if the beam splitter is 50:50 then the probabilities of each output are equal, i.e. [math]\displaystyle{ \hat{a}^\dagger |0\rangle_a \to \frac{1}{\sqrt{2}}\left( \hat{c}^\dagger + \hat{d}^\dagger\right)|00\rangle_{cd} }[/math], and similarly for inserting a photon in b. Therefore

[math]\displaystyle{ \hat{a}^\dagger \to \frac{\hat{c}^\dagger + \hat{d}^\dagger}{\sqrt{2}} \quad\text{and}\quad \hat{b}^\dagger \to \frac{\hat{c}^\dagger - \hat{d}^\dagger}{\sqrt{2}}. }[/math]

The relative minus sign appears because the classical lossless beam splitter produces a unitary transformation. This can be seen most clearly when we write the two-mode beam splitter transformation in matrix form:

[math]\displaystyle{ \begin{pmatrix} \hat{a} \\ \hat{b} \end{pmatrix} \to \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} \hat{c} \\ \hat{d} \end{pmatrix}. }[/math]

Similar transformations hold for the creation operators. Unitarity of the transformation implies unitarity of the matrix. Physically, this beam splitter transformation means that reflection from one surface induces a relative phase shift of π, corresponding to a factor of −1, with respect to reflection from the other side of the beam splitter (see the Physical description above).

When two photons enter the beam splitter, one on each side, the state of the two modes becomes

[math]\displaystyle{ |1, 1\rangle_{ab} = \hat{a}^\dagger \hat{b}^\dagger |0, 0\rangle_{ab} \to \frac{1}{2} \left( \hat{c}^\dagger + \hat{d}^\dagger \right) \left( \hat{c}^\dagger - \hat{d}^\dagger \right) |0, 0\rangle_{cd} }[/math]
[math]\displaystyle{ = \frac{1}{2} \left( \hat{c}^{\dagger 2} - \hat{d}^{\dagger 2} \right) |0, 0\rangle_{cd} = \frac{|2, 0\rangle_{cd} - |0, 2\rangle_{cd}}{\sqrt{2}}, }[/math]

where we used [math]\displaystyle{ \hat{c}^{\dagger 2}|0, 0\rangle_{cd}=\hat{c}^\dagger|1, 0\rangle_{cd}=\sqrt{2}|2, 0\rangle_{cd} }[/math] etc. Since the commutator of the two creation operators [math]\displaystyle{ \hat{c}^\dagger }[/math] and [math]\displaystyle{ \hat{d}^\dagger }[/math] is zero because they operate on different spaces, the product term vanishes. The surviving terms in the superposition are only the [math]\displaystyle{ \hat{c}^{\dagger 2} }[/math] and [math]\displaystyle{ \hat{d}^{\dagger 2} }[/math] terms. Therefore, when two identical photons enter a 1:1 beam splitter, they will always exit the beam splitter in the same (but random) output mode.

The result is non-classical: a classical light wave entering a classical beam splitter with the same transfer matrix would always exit in arm c due to destructive interference in arm d, whereas the quantum result is random. Changing the beam splitter phases can change the classical result to arm d or a mixture of both, but the quantum result is independent of these phases.

For a more general treatment of the beam splitter with arbitrary reflection/transmission coefficients, and arbitrary numbers of input photons, see the general quantum mechanical treatment of a beamsplitter for the resulting output Fock state.

Experimental signature

The "HOM dip" of coincident counts in the detectors versus relative delay between single-photon wave packets

Customarily the Hong–Ou–Mandel effect is observed using two photodetectors monitoring the output modes of the beam splitter. The coincidence rate of the detectors will drop to zero when the identical input photons overlap perfectly in time. This is called the Hong–Ou–Mandel dip, or HOM dip. The coincidence count reaches a minimum, indicated by the dotted line. The minimum drops to zero when the two photons are perfectly identical in all properties. When the two photons are perfectly distinguishable, the dip completely disappears. The precise shape of the dip is directly related to the power spectrum of the single-photon wave packet and is therefore determined by the physical process of the source. Common shapes of the HOM dip are Gaussian and Lorentzian.

A classical analogue to the HOM effect occurs when two coherent states (e.g. laser beams) interfere at the beamsplitter. If the states have a rapidly varying phase difference (i.e. faster than the integration time of the detectors) then a dip will be observed in the coincidence rate equal to one half the average coincidence count at long delays. (Nevertheless, it can be further reduced with a proper discriminating trigger level applied to the signal.) Consequently, to prove that destructive interference is two-photon quantum interference rather than a classical effect, the HOM dip must be lower than one half.

The Hong–Ou–Mandel effect can be directly observed using single-photon-sensitive intensified cameras. Such cameras have the ability to register single photons as bright spots clearly distinguished from the low-noise background.

Direct observation of HOM effect using intensified camera. Coalescing photon pairs appear together as bright spots in one of beam-splitter output ports (left or right pane).[3]

In the figure above, the pairs of photons are registered in the middle of the Hong–Ou–Mandel dip.[3] In most cases, they appear grouped in pairs either on the left or right side, corresponding to two output ports of a beam splitter. Occasionally a coincidence event occurs, manifesting a residual distinguishability between the photons.

Applications and experiments

The Hong–Ou–Mandel effect can be used to test the degree of indistinguishability of the two incoming photons. When the HOM dip reaches all the way down to zero coincident counts, the incoming photons are perfectly indistinguishable, whereas if there is no dip, the photons are distinguishable. In 2002, the Hong–Ou–Mandel effect was used to demonstrate the purity of a solid-state single-photon source by feeding two successive photons from the source into a 1:1 beam splitter.[4] The interference visibility V of the dip is related to the states of the two photons [math]\displaystyle{ \rho_a }[/math] and [math]\displaystyle{ \rho_b }[/math] as

[math]\displaystyle{ V = \operatorname{Tr}(\rho_{a} \rho_{b}). }[/math]

If [math]\displaystyle{ \rho_a = \rho_b = \rho }[/math], then the visibility is equal to the purity [math]\displaystyle{ P = \operatorname{Tr}(\rho^2) }[/math] of the photons.[5] In 2006, an experiment was performed in which two atoms independently emitted a single photon each. These photons subsequently produced the Hong–Ou–Mandel effect.[6]

Multimode Hong–Ou–Mandel interference was studied in 2003. [7]

The Hong–Ou–Mandel effect also underlies the basic entangling mechanism in linear optical quantum computing, and the two-photon quantum state [math]\displaystyle{ |2,0\rangle + |0,2\rangle }[/math] that leads to the HOM dip is the simplest non-trivial state in a class called NOON states.

In 2015 the Hong–Ou–Mandel effect for photons was directly observed with spatial resolution using an sCMOS camera with an image intensifier.[3] Also in 2015 the effect was observed with helium-4 atoms.[8]

The HOM effect can be used to measure the biphoton wave function from a spontaneous four-wave mixing process.[9]

In 2016 a frequency converter for photons demonstrated the Hong–Ou–Mandel effect with different-color photons.[10]

In 2018, HOM interference was used to demonstrate high-fidelity quantum interference between topologically protected states on a photonic chip.[11] Topological photonics have intrinsically high-coherence, and unlike other quantum processor approaches, do not require strong magnetic fields and operate at room temperature.

Three-photon interference

Three-photon interference effect has been identified in experiments.[12][13][14][15]

See also

References

  1. ↑ C. K. Hong; Z. Y. Ou; L. Mandel (1987). "Measurement of subpicosecond time intervals between two photons by interference". Phys. Rev. Lett. 59 (18): 2044–2046. doi:10.1103/PhysRevLett.59.2044. PMID 10035403. Bibcode: 1987PhRvL..59.2044H. 
  2. ↑ Knill, E.; Laflamme, R.; Milburn, G. J. (2001). "A scheme for efficient quantum computation with linear optics". Nature 409 (6816): 46–52. doi:10.1038/35051009. PMID 11343107. Bibcode: 2001Natur.409...46K. 
  3. ↑ 3.0 3.1 3.2 M. Jachura; R. Chrapkiewicz (2015). "Shot-by-shot imaging of Hong–Ou–Mandel interference with an intensified sCMOS camera". Opt. Lett. 40 (7): 1540–1543. doi:10.1364/ol.40.001540. PMID 25831379. Bibcode: 2015OptL...40.1540J. 
  4. ↑ C. Santori; D. Fattal; J. Vucković; G. S. Solomon; Y. Yamamoto (2002). "Indistinguishable photons from a single-photon device". Nature 419 (6907): 594–597. doi:10.1038/nature01086. PMID 12374958. Bibcode: 2002Natur.419..594S. 
  5. ↑ Jachura, Michał; Chrapkiewicz, Radosław (2017). "Hong-Ou-Mandel Interference". arXiv:1711.00080 [quant-ph].
  6. ↑ J. Beugnon; M. P. A. Jones; J. Dingjan; B. Darquié; G. Messin; A. Browaeys; P. Grangier (2006). "Quantum interference between two single photons emitted by independently trapped atoms". Nature 440 (7085): 779–782. doi:10.1038/nature04628. PMID 16598253. Bibcode: 2006Natur.440..779B. 
  7. ↑ Walborn, S. P.; Oliveira, A. N.; Pádua, S.; Monken, C. H. (8 April 2003). "Multimode Hong-Ou-Mandel Interference". Phys. Rev. Lett. 90 (14): 143601. doi:10.1103/PhysRevLett.90.143601. PMID 12731915. Bibcode: 2003PhRvL..90n3601W. 
  8. ↑ R. Lopes; A. Imanaliev; A. Aspect; M. Cheneau; D. Boiron; C. I. Westbrook (2015). "Atomic Hong–Ou–Mandel experiment". Nature 520 (7545): 66–68. doi:10.1038/nature14331. PMID 25832404. Bibcode: 2015Natur.520...66L. 
  9. ↑ P. Chen; C. Shu; X. Guo; M. M. T. Loy; S. Du (2015). "Measuring the biphoton temporal wave function with polarization-dependent and time-resolved two-photon interference". Phys. Rev. Lett. 114 (1): 010401. doi:10.1103/PhysRevLett.114.010401. PMID 25615453. Bibcode: 2015PhRvL.114a0401C. http://repository.ust.hk/ir/bitstream/1783.1-67514/1/PhysRevLett.114.010401.pdf. 
  10. ↑ T. Kobayashi; R. Ikuta; S. Yasui; S. Miki; T. Yamashita; H. Terai; T. Yamamoto; M. Koashi et al. (2016). "Frequency-domain Hong–Ou–Mandel interference". Nature Photonics 10 (7): 441–444. doi:10.1038/nphoton.2016.74. Bibcode: 2016NaPho..10..441K. 
  11. ↑ Jean-Luc Tambasco; Giacomo Corrielli; Robert J. Chapman; Andrea Crespi; Oded Zilberberg; Roberto Osellame; Alberto Peruzzo (2018). "Quantum interference of topological states of light". Science Advances (American Association for the Advancement of Science) 4 (9): eaat3187. doi:10.1126/sciadv.aat3187. PMID 30225365. Bibcode: 2018SciA....4.3187T. 
  12. ↑ Tillmann, Max; Tan, Si-Hui; Stoeckl, Sarah E.; Sanders, Barry C.; de Guise, Hubert; Heilmann, René; Nolte, Stefan; Szameit, Alexander et al. (2015-10-27). "Generalized Multiphoton Quantum Interference". Physical Review X 5 (4): 041015. doi:10.1103/PhysRevX.5.041015. Bibcode: 2015PhRvX...5d1015T. 
  13. ↑ Sewell, Robert (2017-04-10). "Viewpoint: Photonic Hat Trick" (in en-US). Physics 10: 38. doi:10.1103/physics.10.38. https://physics.aps.org/articles/v10/38. 
  14. ↑ Agne, Sascha; Kauten, Thomas; Jin, Jeongwan; Meyer-Scott, Evan; Salvail, Jeff Z.; Hamel, Deny R.; Resch, Kevin J.; Weihs, Gregor et al. (2017-04-10). "Observation of Genuine Three-Photon Interference". Physical Review Letters 118 (15): 153602. doi:10.1103/PhysRevLett.118.153602. PMID 28452530. Bibcode: 2017PhRvL.118o3602A. 
  15. ↑ Menssen, Adrian J.; Jones, Alex E.; Metcalf, Benjamin J.; Tichy, Malte C.; Barz, Stefanie; Kolthammer, W. Steven; Walmsley, Ian A. (2017-04-10). "Distinguishability and Many-Particle Interference". Physical Review Letters 118 (15): 153603. doi:10.1103/PhysRevLett.118.153603. PMID 28452506. Bibcode: 2017PhRvL.118o3603M. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Hong–Ou–Mandel_effect&oldid=3277161"