Linear optical quantum computing

From HandWiki
Short description: Paradigm of quantum computer

Linear optical quantum computing or linear optics quantum computation (LOQC), also photonic quantum computing (PQC), is a paradigm of quantum computation, allowing (under certain conditions, described below) universal quantum computation. LOQC uses photons as information carriers, mainly uses linear optical elements, or optical instruments (including reciprocal mirrors and waveplates) to process quantum information, and uses photon detectors and quantum memories to detect and store quantum information.[1][2][3]

Overview

Although there are many other implementations for quantum information processing (QIP) and quantum computation, optical quantum systems are prominent candidates, since they link quantum computation and quantum communication in the same framework. In optical systems for quantum information processing, the unit of light in a given mode—or photon—is used to represent a qubit. Superpositions of quantum states can be easily represented, encrypted, transmitted and detected using photons. Besides, linear optical elements of optical systems may be the simplest building blocks to realize quantum operations and quantum gates. Each linear optical element equivalently applies a unitary transformation on a finite number of qubits. The system of finite linear optical elements constructs a network of linear optics, which can realize any quantum circuit diagram or quantum network based on the quantum circuit model. Quantum computing with continuous variables is also possible under the linear optics scheme.[4]

The universality of 1- and 2-bit gates to implement arbitrary quantum computation has been proven.[5][6][7][8] Up to [math]\displaystyle{ N\times N }[/math] unitary matrix operations ([math]\displaystyle{ U(N) }[/math]) can be realized by only using mirrors, beam splitters and phase shifters[9] (this is also a starting point of boson sampling and of computational complexity analysis for LOQC). It points out that each [math]\displaystyle{ U(N) }[/math] operator with [math]\displaystyle{ N }[/math] inputs and [math]\displaystyle{ N }[/math] outputs can be constructed via [math]\displaystyle{ \mathcal{O}(N^2) }[/math] linear optical elements. Based on the reason of universality and complexity, LOQC usually only uses mirrors, beam splitters, phase shifters and their combinations such as Mach–Zehnder interferometers with phase shifts to implement arbitrary quantum operators. If using a non-deterministic scheme, this fact also implies that LOQC could be resource-inefficient in terms of the number of optical elements and time steps needed to implement a certain quantum gate or circuit, which is a major drawback of LOQC.

Operations via linear optical elements (beam splitters, mirrors and phase shifters, in this case) preserve the photon statistics of input light. For example, a coherent (classical) light input produces a coherent light output; a superposition of quantum states input yields a quantum light state output.[3] Due to this reason, people usually use single photon source case to analyze the effect of linear optical elements and operators. Multi-photon cases can be implied through some statistical transformations.

An intrinsic problem in using photons as information carriers is that photons hardly interact with each other. This potentially causes a scalability problem for LOQC, since nonlinear operations are hard to implement, which can increase the complexity of operators and hence can increase the resources required to realize a given computational function. One way to solve this problem is to bring nonlinear devices into the quantum network. For instance, the Kerr effect can be applied into LOQC to make a single-photon controlled-NOT and other operations.[10][11]

KLM protocol

Main page: KLM protocol

It was believed that adding nonlinearity to the linear optical network was sufficient to realize efficient quantum computation.[12] However, to implement nonlinear optical effects is a difficult task. In 2000, Knill, Laflamme and Milburn proved that it is possible to create universal quantum computers solely with linear optical tools.[2] Their work has become known as the "KLM scheme" or "KLM protocol", which uses linear optical elements, single photon sources and photon detectors as resources to construct a quantum computation scheme involving only ancilla resources, quantum teleportations and error corrections. It uses another way of efficient quantum computation with linear optical systems, and promotes nonlinear operations solely with linear optical elements.[3]

At its root, the KLM scheme induces an effective interaction between photons by making projective measurements with photodetectors, which falls into the category of non-deterministic quantum computation. It is based on a non-linear sign shift between two qubits that uses two ancilla photons and post-selection.[13] It is also based on the demonstrations that the probability of success of the quantum gates can be made close to one by using entangled states prepared non-deterministically and quantum teleportation with single-qubit operations[14][15] Otherwise, without a high enough success rate of a single quantum gate unit, it may require an exponential amount of computing resources. Meanwhile, the KLM scheme is based on the fact that proper quantum coding can reduce the resources for obtaining accurately encoded qubits efficiently with respect to the accuracy achieved, and can make LOQC fault-tolerant for photon loss, detector inefficiency and phase decoherence. As a result, LOQC can be robustly implemented through the KLM scheme with a low enough resource requirement to suggest practical scalability, making it as promising a technology for QIP as other known implementations.

Boson sampling

Main page: Boson sampling

The more limited boson sampling model was suggested and analyzed by Aaronson and Arkhipov in 2010.[16] It is not believed to be universal,[16] but can still solve problems that are believed to be beyond the ability of classical computers, such as the boson sampling problem. On Dec 3 2020 a team led by Chinese Physicist Pan Jianwei (潘建伟) and Lu Chaoyang (陆朝阳) from University of Science and Technology of China in Hefei, Anhui Province submitted their results to Science in which they solved a problem that is virtually unassailable by any classical computer; thereby proving Quantum supremacy of their photon-based quantum computer called Jiu Zhang Quantum Computer (九章量子计算机).[17] The boson sampling problem was solved in 200 seconds, they estimated that China's Sunway TaihuLight Supercomputer would take 2.5 billion years to solve - a quantum supremacy of around 10^14. Jiu Zhang was named in honor of China's oldest surviving mathematical text (Jiǔ zhāng suàn shù) The Nine Chapters on the Mathematical Art[18]

Ingredients

DiVincenzo's criteria for quantum computation and QIP[19][20] give that a universal system for QIP should satisfy at least the following requirements:

  1. a scalable physical system with well characterized qubits,
  2. the ability to initialize the state of the qubits to a simple fiducial state, such as [math]\displaystyle{ |000\cdots\rangle }[/math],
  3. long relevant decoherence times, much longer than the gate operation time,
  4. a "universal" set of quantum gates (this requirement cannot be satisfied by a non-universal system),
  5. a qubit-specific measurement capability;
    if the system is also aiming for quantum communication, it should also satisfy at least the following two requirements:
  6. the ability to interconvert stationary and flying qubits, and
  7. the ability to faithfully transmit flying qubits between specified location.

As a result of using photons and linear optical circuits, in general LOQC systems can easily satisfy conditions 3, 6 and 7.[3] The following sections mainly focus on the implementations of quantum information preparation, readout, manipulation, scalability and error corrections, in order to discuss the advantages and disadvantages of LOQC as a candidate for QIP

Qubits and modes

A qubit is one of the fundamental QIP units. A qubit state which can be represented by [math]\displaystyle{ \alpha |0\rangle + \beta|1\rangle }[/math] is a superposition state which, if measured in the orthonormal basis [math]\displaystyle{ \{|0\rangle, |1\rangle\} }[/math], has probability [math]\displaystyle{ |\alpha|^2 }[/math] of being in the [math]\displaystyle{ |0\rangle }[/math] state and probability [math]\displaystyle{ |\beta|^2 }[/math] of being in the [math]\displaystyle{ |1\rangle }[/math] state, where [math]\displaystyle{ |\alpha|^2+|\beta|^2=1 }[/math] is the normalization condition. An optical mode is a distinguishable optical communication channel, which is usually labeled by subscripts of a quantum state. There are many ways to define distinguishable optical communication channels. For example, a set of modes could be different polarization of light which can be picked out with linear optical elements, various frequencies, or a combination of the two cases above.

In the KLM protocol, each of the photons is usually in one of two modes, and the modes are different between the photons (the possibility that a mode is occupied by more than one photon is zero). This is not the case only during implementations of controlled quantum gates such as CNOT. When the state of the system is as described, the photons can be distinguished, since they are in different modes, and therefore a qubit state can be represented using a single photon in two modes, vertical (V) and horizontal (H): for example, [math]\displaystyle{ |0\rangle \equiv |0,1\rangle _{VH} }[/math] and [math]\displaystyle{ |1\rangle \equiv |1,0\rangle _{VH} }[/math]. It is common to refer to the states defined via occupation of modes as Fock states.

In boson sampling, photons are not distinguished, and therefore cannot directly represent the qubit state. Instead, we represent the qubit state of the entire quantum system by using the Fock states of [math]\displaystyle{ M }[/math] modes which are occupied by [math]\displaystyle{ N }[/math] indistinguishable single photons (this is a [math]\displaystyle{ \tbinom {M+N-1} {M} }[/math]-level quantum system).

State preparation

To prepare a desired multi-photon quantum state for LOQC, a single-photon state is first required. Therefore, non-linear optical elements, such as single-photon generators and some optical modules, will be employed. For example, optical parametric down-conversion can be used to conditionally generate the [math]\displaystyle{ |1\rangle \equiv |1,0\rangle _{VH} }[/math] state in the vertical polarization channel at time [math]\displaystyle{ t }[/math] (subscripts are ignored for this single qubit case). By using a conditional single-photon source, the output state is guaranteed, although this may require several attempts (depending on the success rate). A joint multi-qubit state can be prepared in a similar way. In general, an arbitrary quantum state can be generated for QIP with a proper set of photon sources.

Implementations of elementary quantum gates

To achieve universal quantum computing, LOQC should be capable of realizing a complete set of universal gates. This can be achieved in the KLM protocol but not in the boson sampling model.

Ignoring error correction and other issues, the basic principle in implementations of elementary quantum gates using only mirrors, beam splitters and phase shifters is that by using these linear optical elements, one can construct any arbitrary 1-qubit unitary operation; in other words, those linear optical elements support a complete set of operators on any single qubit.

The unitary matrix associated with a beam splitter [math]\displaystyle{ \mathbf{B}_{\theta,\phi} }[/math] is:

[math]\displaystyle{ U(\mathbf{B}_{\theta,\phi}) =\begin{bmatrix} \cos \theta & -e^{i\phi}\sin \theta \\ e^{-i\phi} \sin \theta & \cos \theta \end{bmatrix} }[/math],

where [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math] are determined by the reflection amplitude [math]\displaystyle{ r }[/math] and the transmission amplitude [math]\displaystyle{ t }[/math] (relationship will be given later for a simpler case). For a symmetric beam splitter, which has a phase shift [math]\displaystyle{ \phi=\frac{\pi}{2} }[/math] under the unitary transformation condition [math]\displaystyle{ |t|^2+|r|^2=1 }[/math] and [math]\displaystyle{ t^*r+tr^*=0 }[/math], one can show that

[math]\displaystyle{ U(\mathbf{B}_{\theta,\phi=\frac{\pi}{2}}) =\begin{bmatrix} t & r\\ r & t\end{bmatrix} =\begin{bmatrix} \cos \theta & -i\sin \theta \\ -i \sin \theta & \cos \theta \end{bmatrix}=\cos \theta \hat{I}-i \sin \theta \hat{\sigma}_x=e^{-i\theta\hat{\sigma}_x} }[/math],

which is a rotation of the single qubit state about the [math]\displaystyle{ x }[/math]-axis by [math]\displaystyle{ 2\theta=2\cos^{-1}(|t|) }[/math] in the Bloch sphere.

A mirror is a special case where the reflecting rate is 1, so that the corresponding unitary operator is a rotation matrix given by

[math]\displaystyle{ R(\theta) = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{bmatrix} }[/math].

For most cases of mirrors used in QIP, the incident angle [math]\displaystyle{ \theta=45^\circ }[/math].

Similarly, a phase shifter operator [math]\displaystyle{ \mathbf{P}_\phi }[/math] associates with a unitary operator described by [math]\displaystyle{ U(\mathbf{P}_\phi)=e^{i\phi} }[/math], or, if written in a 2-mode format

[math]\displaystyle{ U(\mathbf{P}_{\phi})= \begin{bmatrix} e^{i\phi} & 0 \\ 0 & 1 \end{bmatrix}=\begin{bmatrix} e^{i\phi/2} & 0\\ 0 & e^{-i\phi/2}\end{bmatrix} \text{(global phase ignored )}=e^{i\frac{\phi}{2} \hat{\sigma}_z} }[/math],

which is equivalent to a rotation of [math]\displaystyle{ -\phi }[/math] about the [math]\displaystyle{ z }[/math]-axis.

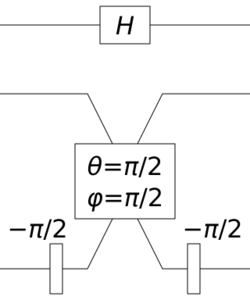
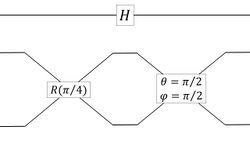
Since any two [math]\displaystyle{ SU(2) }[/math] rotations along orthogonal rotating axes can generate arbitrary rotations in the Bloch sphere, one can use a set of symmetric beam splitters and mirrors to realize an arbitrary [math]\displaystyle{ SU(2) }[/math] operators for QIP. The figures below are examples of implementing a Hadamard gate and a Pauli-X-gate (NOT gate) by using beam splitters (illustrated as rectangles connecting two sets of crossing lines with parameters [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math]) and mirrors (illustrated as rectangles connecting two sets of crossing lines with parameter [math]\displaystyle{ R(\theta) }[/math]).

Implementation of a Hadamard gate with a beam splitter and a mirror. Quantum circuit is on the top part.
Implementation of a Pauli-X gate (NOT gate) with a beam splitter. Quantum circuit is on the top part.

In the above figures, a qubit is encoded using two mode channels (horizontal lines): [math]\displaystyle{ \left\vert0\right\rangle }[/math] represents a photon in the top mode, and [math]\displaystyle{ \left\vert1\right\rangle }[/math] represents a photon in the bottom mode.

Using integrated photonic circuits

In reality, assembling a whole bunch (possibly on the order of [math]\displaystyle{ 10^4 }[/math][21]) of beam splitters and phase shifters in an optical experimental table is challenging and unrealistic. To make LOQC functional, useful and compact, one solution is to miniaturize all linear optical elements, photon sources and photon detectors, and to integrate them onto a chip. If using a semiconductor platform, single photon sources and photon detectors can be easily integrated. To separate modes, there have been integrated arrayed waveguide grating (AWG) which are commonly used as optical (de)multiplexers in wavelength division multiplexed (WDM). In principle, beam splitters and other linear optical elements can also be miniaturized or replaced by equivalent nanophotonics elements. Some progress in these endeavors can be found in the literature, for example, Refs.[22][23][24] In 2013, the first integrated photonic circuit for quantum information processing has been demonstrated using photonic crystal waveguide to realize the interaction between guided field and atoms.[25]

Implementations comparison

Comparison of the KLM protocol and the boson sampling model

The advantage of the KLM protocol over the boson sampling model is that while the KLM protocol is a universal model, boson sampling is not believed to be universal. On the other hand, it seems that the scalability issues in boson sampling are more manageable than those in the KLM protocol.

In boson sampling only a single measurement is allowed, a measurement of all the modes at the end of the computation. The only scalability problem in this model arises from the requirement that all the photons arrive at the photon detectors within a short-enough time interval and with close-enough frequencies.[16]

In the KLM protocol, there are non-deterministic quantum gates, which are essential for the model to be universal. These rely on gate teleportation, where multiple probabilistic gates are prepared offline and additional measurements are performed mid-circuit. Those two factors are the cause for additional scalability problems in the KLM protocol.

In the KLM protocol the desired initial state is one in which each of the photons is in one of two modes, and the possibility that a mode is occupied by more than one photon is zero. In boson sampling, however, the desired initial state is specific, requiring that the first [math]\displaystyle{ N }[/math] modes are each occupied by a single photon[16] ([math]\displaystyle{ N }[/math] is the number of photons and [math]\displaystyle{ M \ge N }[/math] is the number of modes) and all the other states are empty.

Earlier models

Another, earlier model which relies on the representation of several qubits by a single photon is based on the work of C. Adami and N. J. Cerf.[1] By using both the location and the polarization of photons, a single photon in this model can represent several qubits; however, as a result, CNOT-gate can only be implemented between the two qubits represented by the same photon.

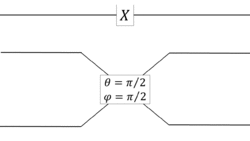
The figures below are examples of making an equivalent Hadamard-gate and CNOT-gate using beam splitters (illustrated as rectangles connecting two sets of crossing lines with parameters [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math]) and phase shifters (illustrated as rectangles on a line with parameter [math]\displaystyle{ \phi }[/math]).

Implementation of Hadamard-gate on a "location" qubit with a beam splitter and phase shifters. Quantum circuit is on the top part.
Implementation of Controlled-NOT-gate with a beam splitter. Quantum circuit is on the top part.

In the optical realization of the CNOT gate, the polarization and location are the control and target qubit, respectively.

References

  1. ↑ 1.0 1.1 Adami, C.; Cerf, N. J. (1999). "Quantum Computation with Linear Optics". Quantum Computing and Quantum Communications. Lecture Notes in Computer Science. 1509. Springer. pp. 391–401. doi:10.1007/3-540-49208-9_36. ISBN 978-3-540-65514-5. 
  2. ↑ 2.0 2.1 Knill, E.; Laflamme, R.; Milburn, G. J. (2001). "A scheme for efficient quantum computation with linear optics". Nature 409 (6816): 46–52. doi:10.1038/35051009. PMID 11343107. Bibcode: 2001Natur.409...46K. 
  3. ↑ 3.0 3.1 3.2 3.3 Kok, P.; Munro, W. J.; Nemoto, K.; Ralph, T. C.; Dowling, J. P.; Milburn, G. J. (2007). "Linear optical quantum computing with photonic qubits". Rev. Mod. Phys. 79 (1): 135–174. doi:10.1103/RevModPhys.79.135. Bibcode: 2007RvMP...79..135K. 
  4. ↑ Lloyd, S.; Braunstein, S. L. (2003). "Quantum computation over continuous variables". Physical Review Letters 82 (8): 9–17. doi:10.1103/PhysRevLett.82.1784. Bibcode: 1999PhRvL..82.1784L. 
  5. ↑ DiVincenzo, David P. (1995-02-01). "Two-bit gates are universal for quantum computation". Physical Review A 51 (2): 1015–1022. doi:10.1103/PhysRevA.51.1015. PMID 9911679. Bibcode: 1995PhRvA..51.1015D. 
  6. ↑ Deutsch, David; Barenco, Adriano; Ekert, Artur (1995-06-08). "Universality in Quantum Computation". Proceedings of the Royal Society of London A: Mathematical and Physical Sciences 449 (1937): 669–677. doi:10.1098/rspa.1995.0065. ISSN 1471-2946. Bibcode: 1995RSPSA.449..669D. 
  7. ↑ Barenco, Adriano (1995-06-08). "A Universal Two-Bit Gate for Quantum Computation". Proceedings of the Royal Society of London A: Mathematical and Physical Sciences 449 (1937): 679–683. doi:10.1098/rspa.1995.0066. ISSN 1471-2946. Bibcode: 1995RSPSA.449..679B. 
  8. ↑ Lloyd, Seth (1995-07-10). "Almost Any Quantum Logic Gate is Universal". Physical Review Letters 75 (2): 346–349. doi:10.1103/PhysRevLett.75.346. PMID 10059671. Bibcode: 1995PhRvL..75..346L. 
  9. ↑ Reck, Michael; Zeilinger, Anton; Bernstein, Herbert J.; Bertani, Philip (1994-07-04). "Experimental realization of any discrete unitary operator". Physical Review Letters 73 (1): 58–61. doi:10.1103/PhysRevLett.73.58. PMID 10056719. Bibcode: 1994PhRvL..73...58R. https://zenodo.org/record/3452285. 
  10. ↑ Milburn, G. J. (1989-05-01). "Quantum optical Fredkin gate". Physical Review Letters 62 (18): 2124–2127. doi:10.1103/PhysRevLett.62.2124. PMID 10039862. Bibcode: 1989PhRvL..62.2124M. http://espace.library.uq.edu.au/view/UQ:247726/UQ247726.pdf. 
  11. ↑ Hutchinson, G. D.; Milburn, G. J. (2004). "Nonlinear quantum optical computing via measurement". Journal of Modern Optics 51 (8): 1211–1222. doi:10.1080/09500340408230417. ISSN 0950-0340. Bibcode: 2004JMOp...51.1211H. 
  12. ↑ Lloyd, Seth (1992-07-20). "Any nonlinear gate, with linear gates, suffices for computation". Physics Letters A 167 (3): 255–260. doi:10.1016/0375-9601(92)90201-V. ISSN 0375-9601. Bibcode: 1992PhLA..167..255L. https://zenodo.org/record/1258495. 
  13. ↑ Adleman, Leonard M.; DeMarrais, Jonathan; Huang, Ming-Deh A. (1997). "Quantum Computability". SIAM Journal on Computing 26 (5): 1524–1540. doi:10.1137/S0097539795293639. ISSN 0097-5397. 
  14. ↑ Bennett, Charles H.; Brassard, Gilles; Crépeau, Claude; Jozsa, Richard; Peres, Asher; Wootters, William K. (1993-03-29). "Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels". Physical Review Letters 70 (13): 1895–1899. doi:10.1103/PhysRevLett.70.1895. PMID 10053414. Bibcode: 1993PhRvL..70.1895B. 
  15. ↑ Gottesman, Daniel; Chuang, Isaac L. (1999-11-25). "Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations". Nature 402 (6760): 390–393. doi:10.1038/46503. ISSN 0028-0836. Bibcode: 1999Natur.402..390G. 
  16. ↑ 16.0 16.1 16.2 16.3 Aaronson, Scott; Arkhipov, Alex (2013). "The computational complexity of linear optics". Theory of Computing 9: 143–252. doi:10.4086/toc.2013.v009a004. 
  17. ↑ Ball, Philip (2020). "Physicists in China challenge Google's 'quantum advantage'". Nature 588 (7838): 380. doi:10.1038/d41586-020-03434-7. PMID 33273711. Bibcode: 2020Natur.588..380B. https://www.nature.com/articles/d41586-020-03434-7. 
  18. ↑ "China claims quantum computing lead with Jiuzhang photon test, creating machine 'one trillion times faster' than next best supercomputer". SCMP. https://www.scmp.com/news/china/science/article/3112649/china-claims-quantum-computing-lead-jiuzhang-photon-test.. 
  19. ↑ DiVincenzo, D.; Loss, D. (1998). "Quantum information is physical". Superlattices and Microstructures 23 (3–4): 419–432. doi:10.1006/spmi.1997.0520. Bibcode: 1998SuMi...23..419D. 
  20. ↑ Divincenzo, D. P. (2000). "The Physical Implementation of Quantum Computation". Fortschritte der Physik 48 (9–11): 771–783. doi:10.1002/1521-3978(200009)48:9/11<771::AID-PROP771>3.0.CO;2-E. Bibcode: 2000ForPh..48..771D. 
  21. ↑ Hayes, A. J. F.; Gilchrist, A.; Myers, C. R.; Ralph, T. C. (2004-12-01). "Utilizing encoding in scalable linear optics quantum computing". Journal of Optics B: Quantum and Semiclassical Optics 6 (12): 533–541. doi:10.1088/1464-4266/6/12/008. ISSN 1464-4266. Bibcode: 2004JOptB...6..533H. 
  22. ↑ Gevaux, D (2008). "Optical quantum circuits: To the quantum level". Nature Photonics 2 (6): 337. doi:10.1038/nphoton.2008.92. Bibcode: 2008NaPho...2..337G. 
  23. ↑ Politi, A.; Cryan, M. J.; Rarity, J. G.; Yu, S.; O'Brien, J. L. (2008). "Silica-on-silicon waveguide quantum circuits". Science 320 (5876): 646–649. doi:10.1126/science.1155441. PMID 18369104. Bibcode: 2008Sci...320..646P. 
  24. ↑ Thompson, M. G.; Politi, A.; Matthews, J. C.; O'Brien, J. L. (2011). "Integrated waveguide circuits for optical quantum computing". IET Circuits, Devices & Systems 5 (2): 94–102. doi:10.1049/iet-cds.2010.0108. 
  25. ↑ Goban, A.; Hung, C. -L.; Yu, S. -P.; Hood, J. D.; Muniz, J. A.; Lee, J. H.; Martin, M. J.; McClung, A. C. et al. (2013). "Atom-Light Interactions in Photonic Crystals". Nature Communications 5: 3808. doi:10.1038/ncomms4808. PMID 24806520. Bibcode: 2014NatCo...5.3808G. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Linear_optical_quantum_computing&oldid=3429324"