Physics:Samarium–neodymium dating

From HandWiki
Revision as of 03:15, 5 February 2024 by Jworkorg (talk | contribs) (over-write)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Radiometric dating method useful for determining the ages of rocks and meteorites

Samarium–neodymium dating is a radiometric dating method useful for determining the ages of rocks and meteorites, based on the alpha decay of the long-lived samarium isotope (147Sm) to the stable radiogenic neodymium isotope (143Nd). Neodymium isotope ratios together with samarium-neodymium ratios are used to provide information on the age and source of igneous melts. It is sometimes assumed that at the moment when crustal material is formed from the mantle the neodymium isotope ratio depends only on the time when this event occurred, but thereafter it evolves in a way that depends on the new ratio of samarium to neodymium in the crustal material, which will be different from the ratio in the mantle material. Samarium–neodymium dating allows us to determine when the crustal material was formed.

The usefulness of Sm–Nd dating stems from the fact that these two elements are rare earth elements and are thus, theoretically, not particularly susceptible to partitioning during sedimentation and diagenesis.[1] Fractional crystallisation of felsic minerals changes the Sm/Nd ratio of the resultant materials. This, in turn, influences the rate at which the 143Nd/144Nd ratio increases due to production of radiogenic 143Nd.

In many cases, Sm–Nd and Rb–Sr isotope data are used together.

Sm–Nd radiometric dating

Samarium has five naturally occurring isotopes, and neodymium has seven. The two elements are joined in a parent–daughter relationship by the alpha decay of parent 147Sm to radiogenic daughter 143Nd with a half-life of 1.06×1011 years and by the alpha decay of 146Sm (an almost-extinct radionuclide with a half-life of 1.03(5)×108 years[lower-alpha 1]) to produce 142Nd.

To find the date at which a rock (or group of rocks) formed one can use the method of isochron dating.[6] The Sm-Nd isochron plots the ratio of radiogenic 143Nd to non-radiogenic 144Nd against the ratio of the parent isotope 147Sm to the non-radiogenic isotope 144Nd. 144Nd is used to normalize the radiogenic isotope in the isochron because it is a stable and relatively abundant neodymium isotope.

The Sm-Nd isochron is defined by the following equation:

[math]\displaystyle{ \left(\frac{{}^{143}\mathrm{Nd}}{{}^{144}\mathrm{Nd}}\right)_{\mathrm{present}} = \left(\frac{{}^{143}\mathrm{Nd}}{{}^{144}\mathrm{Nd}}\right)_{\mathrm{initial}} + \left(\frac{{}^{147}\mathrm{Sm}}{{}^{144}\mathrm{Nd}}\right) \cdot (e^{\lambda t}-1), }[/math]

where:

t is the age of the sample,
λ is the decay constant of 147Sm,
(eλt−1) is the slope of the isochron which defines the age of the system.

Alternatively, one can assume that the material formed from mantle material which was following the same path of evolution of these ratios as chondrites, and then again the time of formation can be calculated (see #The CHUR model).[6][1]

Sm and Nd geochemistry

The concentration of Sm and Nd in silicate minerals increase with the order in which they crystallise from a magma according to Bowen's reaction series. Samarium is accommodated more easily into mafic minerals, so a mafic rock which crystallises mafic minerals will concentrate neodymium in the melt phase relative to samarium. Thus, as a melt undergoes fractional crystallization from a mafic to a more felsic composition, the abundance of Sm and Nd changes, as does the ratio between Sm and Nd.

Thus, ultramafic rocks have high Sm and low Nd and therefore high Sm/Nd ratios. Felsic rocks have low concentrations of Sm and high Nd and therefore low Sm/Nd ratios (for example komatiite has 1.14 parts per million (ppm) Sm and 3.59 ppm Nd versus 4.65 ppm Sm and 21.6 ppm Nd in rhyolite).

The importance of this process is apparent in modeling the age of continental crust formation.

The CHUR model

Through the analysis of isotopic compositions of neodymium, DePaolo and Wasserburg (1976[6]) discovered that terrestrial igneous rocks at the time of their formation from melts closely followed the "chondritic uniform reservoir" or "chondritic unifractionated reservoir" (CHUR) line – the way the 143Nd:144Nd ratio increased with time in chondrites. Chondritic meteorites are thought to represent the earliest (unsorted) material that formed in the Solar system before planets formed. They have relatively homogeneous trace-element signatures, and therefore their isotopic evolution can model the evolution of the whole Solar system and of the "bulk Earth". After plotting the ages and initial 143Nd/144Nd ratios of terrestrial igneous rocks on a Nd evolution vs. time diagram, DePaolo and Wasserburg determined that Archean rocks had initial Nd isotope ratios very similar to that defined by the CHUR evolution line.

Epsilon notation

Since 143Nd/144Nd departures from the CHUR evolution line are very small, DePaolo and Wasserburg argued that it would be useful to create a form of notation that described 143Nd/144Nd in terms of their deviations from the CHUR evolution line. This is called the epsilon notation, whereby one epsilon unit represents a one part per 10,000 deviation from the CHUR composition.[7] Algebraically, epsilon units can be defined by the equation

[math]\displaystyle{ \varepsilon_{\text{Nd}(t)} = \left[\frac{\left(\frac{^{143}\text{Nd}}{^{144}\text{Nd}}\right)_{\text{sample}(t)}}{\left(\frac{^{143}\text{Nd}}{^{144}\text{Nd}}\right)_{\text{CHUR}(t)}} - 1\right] \times 10\,000. }[/math]

Since epsilon units are finer and therefore a more tangible representation of the initial Nd isotope ratio, by using these instead of the initial isotopic ratios, it is easier to comprehend and therefore compare initial ratios of crust with different ages. In addition, epsilon units will normalize the initial ratios to CHUR, thus eliminating any effects caused by various analytical mass fractionation correction methods applied.[7]

Nd model ages

Since CHUR defines initial ratios of continental rocks through time, it was deduced that measurements of 143Nd/144Nd and 147Sm/144Nd, with the use of CHUR, could produce model ages for the segregation from the mantle of the melt that formed any crustal rock. This has been termed TCHUR.[1] In order for a TCHUR age to be calculated, fractionation between Nd/Sm would have to have occurred during magma extraction from the mantle to produce a continental rock. This fractionation would then cause a deviation between the crustal and mantle isotopic evolution lines. The intersection between these two evolution lines then indicates the crustal formation age. The TCHUR age is defined by the following equation:

[math]\displaystyle{ T_\text{CHUR} = \left(\frac{1}{\lambda}\right) \ln \left[1 + \frac{\left(\frac{^{143}\text{Nd}}{^{144}\text{Nd}}\right)_\text{sample} - \left(\frac{^{143}\text{Nd}}{^{144}\text{Nd}}\right)_\text{CHUR}}{\left(\frac{^{147}\text{Sm}}{^{144}\text{Nd}}\right)_\text{sample} - \left(\frac{^{147}\text{Sm}}{^{144}\text{Nd}}\right)_\text{CHUR}}\right]. }[/math]

The TCHUR age of a rock can yield a formation age for the crust as a whole if the sample has not suffered disturbance after its formation. Since Sm/Nd are rare-earth elements (REE), their characterisity enables theitic immobile ratios to resist partitioning during metamorphism and melting of silicate rocks. This therefore allows crustal formation ages to be calculated, despite any metamorphism the sample has undergone.

The depleted-mantle model

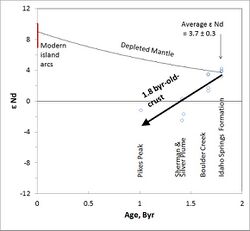
Graph to show the depleted-mantle model of DePaolo (1981)

Despite the good fit of Archean plutons to the CHUR Nd isotope evolution line, DePaolo and Wasserburg (1976) observed that the majority of young oceanic volcanics (Mid Ocean Ridge basalts and Island Arc basalts) lay +7 to +12 ɛ units above the CHUR line (see figure). This led to the realization that Archean continental igneous rocks that plotted within the error of the CHUR line could instead lie on a depleted-mantle evolution line characterized by increasing Sm/Nd and 143Nd/144Nd ratios over time. To further analyze this gap between the Archean CHUR data and the young volcanic samples, a study was conducted on the Proterozoic metamorphic basement of the Colorado Front Ranges (the Idaho Springs Formation).[8] The initial 143Nd/144Nd ratios of the samples analyzed are plotted on a ɛNd versus time diagram shown in the figure. DePaolo (1981) fitted a quadratic curve to the Idaho Springs and average ɛNd for the modern oceanic island arc data, thus representing the neodymium isotope evolution of a depleted reservoir. The composition of the depleted reservoir relative to the CHUR evolution line, at time T, is given by the equation

ɛNd(T) = 0.25 T2 – 3 T + 8.5.

Sm-Nd model ages calculated using this curve are denoted as TDM ages. DePaolo (1981) argued that these TDM model ages would yield a more accurate age for crustal formation ages than TCHUR model ages – for example, an anomalously low TCHUR model age of 0.8 Gy from McCulloch and Wasserburg's Grenville composite was revised to a TDM age of 1.3 Gy, typical for juvenile crust formation during the Grenville orogeny.

See also

Notes

  1. ↑ The value 6.8(7)×107 years was also in use between 2012 and 2023.[2][3][4][5]

References

  1. ↑ 1.0 1.1 1.2 McCulloch, M. T.; Wasserburg, G. J. (1978). "Sm-Nd and Rb-Sr Chronology of Continental Crust Formation". Science 200 (4345): 1003–11. doi:10.1126/science.200.4345.1003. PMID 17740673. Bibcode: 1978Sci...200.1003M. https://resolver.caltech.edu/CaltechAUTHORS:20131107-143832294. 
  2. ↑ Kinoshita, N.; Paul, M.; Kashiv, Y.; Collon, P.; Deibel, C. M.; DiGiovine, B.; Greene, J. P.; Henderson, D. J. et al. (30 March 2012). "A Shorter 146Sm Half-Life Measured and Implications for 146Sm-142Nd Chronology in the Solar System" (in en). Science 335 (6076): 1614–1617. doi:10.1126/science.1215510. ISSN 0036-8075. PMID 22461609. Bibcode: 2012Sci...335.1614K. 
  3. ↑ Villa, I.M.; Holden, N.E.; Possolo, A.; Ickert, R.B.; Hibbert, D.B.; Renne, P.R. (September 2020). "IUPAC-IUGS recommendation on the half-lives of 147Sm and 146Sm". Geochimica et Cosmochimica Acta 285: 70–77. doi:10.1016/j.gca.2020.06.022. ISSN 0016-7037. 
  4. ↑ Kinoshita, N.; Paul, M.; Kashiv, Y.; Collon, P.; Deibel, C. M.; DiGiovine, B.; Greene, J. P.; Jiang, C. L. et al. (30 March 2023). "Retraction". Science 379 (6639): 1307. doi:10.1126/science.adh7739. 
  5. ↑ Joelving, Frederik (30 March 2023). "One small error for a physicist, one giant blunder for planetary science". https://retractionwatch.com/2023/03/30/one-small-error-for-a-physicist-one-giant-blunder-for-planetary-science/. 
  6. ↑ 6.0 6.1 6.2 Depaolo, D. J.; Wasserburg, G. J. (1976). "Nd isotopic variations and petrogenetic models". Geophysical Research Letters 3 (5): 249. doi:10.1029/GL003i005p00249. Bibcode: 1976GeoRL...3..249D. https://authors.library.caltech.edu/41937/1/grl330.pdf. 
  7. ↑ 7.0 7.1 Dickin, A. P., 2005. Radiogenic Isotope Geology, 2nd ed. Cambridge: Cambridge University Press. ISBN:0-521-82316-1 pp. 76–77.
  8. ↑ DePaolo, D. J. (1981). Neodymium isotopes in the Colorado Front Range and crust – mantle evolution in the Proterozoic. Nature 291, 193–197.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Samarium–neodymium_dating&oldid=3277722"