Chemistry:Möbius aromaticity
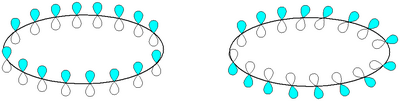
In organic chemistry, Möbius aromaticity is a special type of aromaticity believed to exist in a number of organic molecules.[1][2] In terms of molecular orbital theory these compounds have in common a monocyclic array of molecular orbitals in which there is an odd number of out-of-phase overlaps, the opposite pattern compared to the aromatic character to Hückel systems. The nodal plane of the orbitals, viewed as a ribbon, is a Möbius strip, rather than a cylinder, hence the name. The pattern of orbital energies is given by a rotated Frost circle (with the edge of the polygon on the bottom instead of a vertex), so systems with 4n electrons are aromatic, while those with 4n + 2 electrons are anti-aromatic/non-aromatic. Due to incrementally twisted nature of the orbitals of a Möbius aromatic system, stable Möbius aromatic molecules need to contain at least 8 electrons, although 4 electron Möbius aromatic transition states are well known in the context of the Dewar-Zimmerman framework for pericyclic reactions. Möbius molecular systems were considered in 1964 by Edgar Heilbronner by application of the Hückel method,[3] but the first such isolable compound was not synthesized until 2003 by the group of Rainer Herges.[4] However, the fleeting trans-C9H9+ cation, one conformation of which is shown on the right, was proposed to be a Möbius aromatic reactive intermediate in 1998 based on computational and experimental evidence.
Hückel-Möbius aromaticity
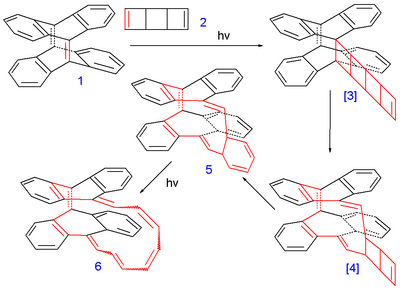
The Herges compound (6 in the image below) was synthesized in several photochemical cycloaddition reactions from tetradehydrodianthracene 1 and the ladderane syn-tricyclooctadiene 2 as a substitute for cyclooctatetraene.[5]
Intermediate 5 was a mixture of 2 isomers and the final product 6 a mixture of 5 isomers with different cis and trans configurations. One of them was found to have a C2 molecular symmetry corresponding to a Möbius aromatic and another Hückel isomer was found with Cs symmetry. Despite having 16 electrons in its pi system (making it a 4n antiaromatic compound) the Heilbronner prediction was borne out because according to Herges the Möbius compound was found to have aromatic properties. With bond lengths deduced from X-ray crystallography a HOMA value was obtained of 0.50 (for the polyene part alone) and 0.35 for the whole compound which qualifies it as a moderate aromat.
It was pointed out by Henry Rzepa that the conversion of intermediate 5 to 6 can proceed by either a Hückel or a Möbius transition state.[6]
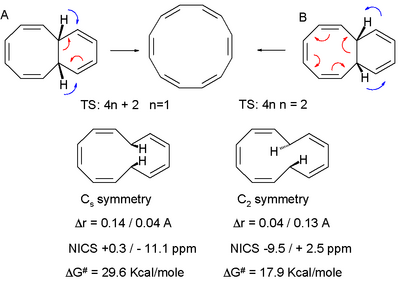
The difference was demonstrated in a hypothetical pericyclic ring opening reaction to cyclododecahexaene. The Hückel TS (left) involves 6 electrons (arrow pushing in red) with Cs molecular symmetry conserved throughout the reaction. The ring opening is disrotatory and suprafacial and both bond length alternation and NICS values indicate that the 6 membered ring is aromatic. The Möbius TS with 8 electrons on the other hand has lower computed activation energy and is characterized by C2 symmetry, a conrotatory and antarafacial ring opening and 8-membered ring aromaticity.
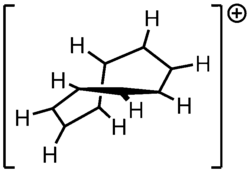
Another interesting system is the cyclononatetraenyl cation explored for over 30 years by Paul v. R. Schleyer et al. This reactive intermediate is implied in the solvolysis of the bicyclic chloride 9-deutero-9'-chlorobicyclo[6.1.0]-nonatriene 1 to the indene dihydroindenol 4.[7][8] The starting chloride is deuterated in only one position but in the final product deuterium is distributed at every available position. This observation is explained by invoking a twisted 8-electron cyclononatetraenyl cation 2 for which a NICS value of -13.4 (outsmarting benzene) is calculated.[9] A more recent study, however, suggests that the stability of trans-C9H9+ is not much different in energy compared to a Hückel topology isomer. The same study suggested that for [13]annulenyl cation, the Möbius topology penta-trans-C13H13+ is a global energy minimum and predicts that it may be directly observable.[10]
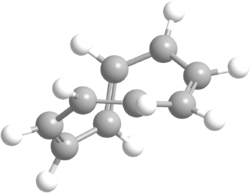 Computed structure of trans-C9H9+, 2, illustrating the twisted nature of the ring, allowing incremental rotation of the orientation of p atomic orbitals around the ring: tracing the p orbitals all the way around the ring results in a phase inversion relative to the starting p orbital. The plane of the carbon skeleton (i.e., the nodal plane of the p orbitals) forms a Möbius strip.
Computed structure of trans-C9H9+, 2, illustrating the twisted nature of the ring, allowing incremental rotation of the orientation of p atomic orbitals around the ring: tracing the p orbitals all the way around the ring results in a phase inversion relative to the starting p orbital. The plane of the carbon skeleton (i.e., the nodal plane of the p orbitals) forms a Möbius strip.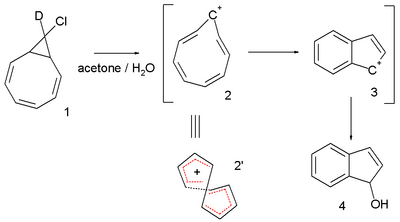
In 2005 the same P. v. R. Schleyer [11] questioned the 2003 Herges claim: he analyzed the same crystallographic data and concluded that there was indeed a large degree of bond length alternation resulting in a HOMA value of -0.02, a computed NICS value of -3.4 ppm also did not point towards aromaticity and (also inferred from a computer model) steric strain would prevent effective pi-orbital overlap.
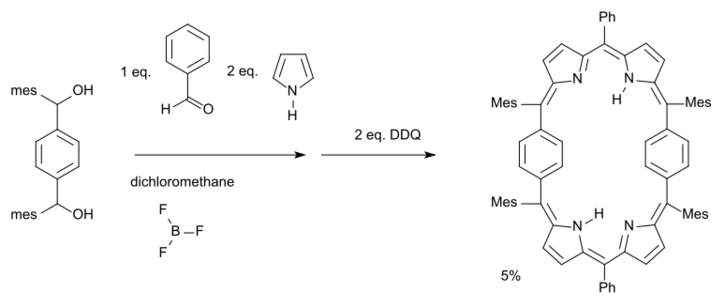
A Hückel-Möbius aromaticity switch (2007) has been described based on a 28 pi-electron porphyrin system:[12][13]
The phenylene rings in this molecule are free to rotate forming a set of conformers: one with a Möbius half-twist and another with a Hückel double-twist (a figure-eight configuration) of roughly equal energy.
In 2014, Zhu and Xia (with the help of Schleyer) synthesized a planar Möbius system that consisted of two pentene rings connected with an osmium atom.[14] They formed derivatives where osmium had 16 and 18 electrons and determined that Craig–Möbius aromaticity is more important for the stabilization of the molecule than the metal's electron count.
Transition states
In contrast to the rarity of Möbius aromatic ground state molecular systems, there are many examples of pericyclic transition states that exhibit Möbius aromaticity. The classification of a pericyclic transition state as either Möbius or Hückel topology determines whether 4N or 4N + 2 electrons are required to make the transition state aromatic or antiaromatic, and therefore, allowed or forbidden, respectively. Based on the energy level diagrams derived from Hückel MO theory, (4N + 2)-electron Hückel and (4N)-electron Möbius transition states are aromatic and allowed, while (4N + 2)-electron Möbius and (4N)-electron Hückel transition states are antiaromatic and forbidden. This is the basic premise of the Möbius-Hückel concept.[15][16]
Derivation of Hückel MO theory energy levels for Möbius topology
From the figure above, it can also be seen that the interaction between two consecutive [math]\displaystyle{ p_z }[/math] AOs is attenuated by the incremental twisting between orbitals by [math]\displaystyle{ \cos\omega }[/math], where [math]\displaystyle{ \omega=\pi/N }[/math] is the angle of twisting between consecutive orbitals, compared to the usual Hückel system. For this reason resonance integral [math]\displaystyle{ \beta^\prime }[/math] is given by
- [math]\displaystyle{ \beta^\prime=\beta\cos(\pi/N) }[/math],
where [math]\displaystyle{ \beta }[/math] is the standard Hückel resonance integral value (with completely parallel orbitals).
Nevertheless, after going all the way around, the Nth and 1st orbitals are almost completely out of phase. (If the twisting were to continue after the [math]\displaystyle{ N }[/math]th orbital, the [math]\displaystyle{ (N+1) }[/math]st orbital would be exactly phase-inverted compared to the 1st orbital). For this reason, in the Hückel matrix the resonance integral between carbon [math]\displaystyle{ 1 }[/math] and [math]\displaystyle{ N }[/math] is [math]\displaystyle{ -\beta^\prime }[/math].
For the generic [math]\displaystyle{ N }[/math] carbon Möbius system, the Hamiltonian matrix [math]\displaystyle{ \mathbf{H} }[/math] is:
- [math]\displaystyle{ \mathbf{H}= \begin{pmatrix} \alpha& \beta' & 0 &\cdots& -\beta' \\ \beta' & \alpha& \beta' & \cdots & 0 \\ 0 & \beta' & \alpha & \cdots & 0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ -\beta' &0& 0 & \cdots & \alpha \end{pmatrix} }[/math].
Eigenvalues for this matrix can now be found, which correspond to the energy levels of the Möbius system. Since [math]\displaystyle{ \mathbf{H} }[/math] is a [math]\displaystyle{ N\times N }[/math] matrix, we will have [math]\displaystyle{ N }[/math] eigenvalues [math]\displaystyle{ E_k }[/math] and [math]\displaystyle{ N }[/math] MOs. Defining the variable
- [math]\displaystyle{ x_k=\frac{\alpha-E_k}{\beta'} }[/math],
we have:
- [math]\displaystyle{ \begin{pmatrix} x_k& 1 & 0 &\cdots& -1 \\ 1 & x_k& 1 & \cdots & 0 \\ 0 & 1 & x_k & \cdots & 0 \\ \vdots &\vdots &\vdots &\ddots &\vdots \\ -1 &0& 0 & \cdots & x_k \end{pmatrix} \cdot \begin{pmatrix} c_1^{(k)} \\ c_2^{(k)} \\ c_3^{(k)} \\ \vdots\\ c_N^{(k)} \\ \end{pmatrix}=0 }[/math].
To find nontrivial solutions to this equation, we set the determinant of this matrix to zero to obtain
- [math]\displaystyle{ x_k=-2\cos{\frac{(2k+1)\pi}{N}} }[/math].
Hence, we find the energy levels for a cyclic system with Möbius topology,
- [math]\displaystyle{ E_k=\alpha+2\beta^\prime\cos{\frac{(2k+1)\pi}{N}}\quad (k=0,1,\ldots, \lceil N/2 \rceil-1) }[/math].
In contrast, recall the energy levels for a cyclic system with Hückel topology,
- [math]\displaystyle{ E_k=\alpha+2\beta\cos{\frac{2k\pi}{N}}\quad (k=0,1,\ldots, \lfloor N/2 \rfloor) }[/math].
See also
References
- ↑ Rzepa, Henry S. (2005). "Möbius Aromaticity and Delocalization". Chem. Rev. 105 (10): 3697–3715. doi:10.1021/cr030092l. PMID 16218564.
- ↑ Seok Yoon, Zin; Osuka, Atsuhiro; Kim, Dongho (2009). "Möbius aromaticity and antiaromaticity in expanded porphyrins". Nature Chemistry 1 (2): 113–122. doi:10.1038/nchem.172. PMID 21378823.
- ↑ Heilbronner, E. (1964). "Hückel molecular orbitals of Möbius-type conformations of annulenes". Tetrahedron Letters 5 (29): 1923–1928. doi:10.1016/S0040-4039(01)89474-0.
- ↑ Ajami, D.; Oeckler, O.; Simon, A.; Herges, R. (December 2003). "Synthesis of a Möbius aromatic hydrocarbon". Nature 426 (6968): 819–821. doi:10.1038/nature02224. PMID 14685233.
- ↑ Note that the Möbius ring is formed in formal olefin metathesis reaction between 1 and COT
- ↑ The Aromaticity of Pericyclic Reaction Transition States Henry S. Rzepa J. Chem. Educ. 2007, 84, 1535. Abstract
- ↑ Paul; Schleyer, R. (1971). "Thermal bicyclo[6.1.0]nonatrienyl chloride-dihydroindenyl chloride rearrangement". Journal of the American Chemical Society 93: 279–281. doi:10.1021/ja00730a063.
- ↑ Herges, Rainer (2006). "Topology in Chemistry: Designing Möbius Molecules †". Chemical Reviews 106 (12): 4820–4842. doi:10.1021/cr0505425. PMID 17165676.
- ↑ Monocyclic (CH)9+ - A Heilbronner Möbius Aromatic System Revealed Angewandte Chemie International Edition Volume 37, Issue 17, Date: September 18, 1998, Pages: 2395-2397 Michael Mauksch, Valentin Gogonea, Haijun Jiao, Paul von Ragué Schleyer
- ↑ Mucke, Eva-Katrin; Köhler, Felix; Herges, Rainer (2010-04-16). "The [13Annulene Cation Is a Stable Möbius Annulene Cation"] (in en). Organic Letters 12 (8): 1708–1711. doi:10.1021/ol1002384. ISSN 1523-7060. PMID 20232816. https://pubs.acs.org/doi/10.1021/ol1002384.
- ↑ Castro, Claire (2005). "Investigation of a Putative Möbius Aromatic Hydrocarbon. The Effect of Benzannelation on Möbius [4 n ]Annulene Aromaticity". Journal of the American Chemical Society 127 (8): 2425–2432. doi:10.1021/ja0458165. PMID 15724997.
- ↑ Stępień, Marcin (2007). "Expanded Porphyrin with a Split Personality: A Hückel–Möbius Aromaticity Switch". Angewandte Chemie International Edition 46 (41): 7869–7873. doi:10.1002/anie.200700555. PMID 17607678.
- ↑ Reagents: pyrrole, benzaldehyde, boron trifluoride, subsequent oxidation with DDQ, Ph = phenyl Mes = mesityl
- ↑ Zhu, Congqing; Ming Luo; Qin Zhu; Jun Zhu; Paul v. R. Schleyer; Judy I-Chia Wu; Xin Lu; Haiping Xia (25 February 2014). "Planar Möbius aromatic pentalenes incorporating 16 and 18 valence electron osmiums.". Nature Communications 5: 3265. doi:10.1038/ncomms4265. PMID 24567039. Bibcode: 2014NatCo...5.3265Z.
- ↑ Zimmerman, H. E (1966). "On Molecular Orbital Correlation Diagrams, the Occurrence of Möbius Systems in Cyclization Reactions, and Factors Controlling Ground and Excited State Reactions. I". J. Am. Chem. Soc. 88 (7): 1564–1565. doi:10.1021/ja00959a052.
- ↑ Zimmerman, H. E (1966). "On Molecular Orbital Correlation Diagrams, Möbius Systems, and Factors Controlling Ground and Excited State Reactions. II". J. Am. Chem. Soc. 88 (7): 1566–1567. doi:10.1021/ja00959a053.
 |