Bipolar coordinates
Bipolar coordinates are a two-dimensional orthogonal coordinate system based on the Apollonian circles.[1] Confusingly, the same term is also sometimes used for two-center bipolar coordinates. There is also a third system, based on two poles (biangular coordinates).
The term "bipolar" is further used on occasion to describe other curves having two singular points (foci), such as ellipses, hyperbolas, and Cassini ovals. However, the term bipolar coordinates is reserved for the coordinates described here, and never used for systems associated with those other curves, such as elliptic coordinates.

Definition
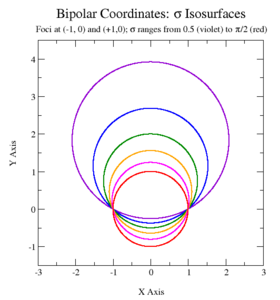
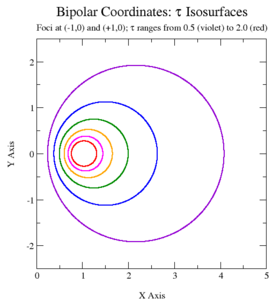
The system is based on two foci F1 and F2. Referring to the figure at right, the σ-coordinate of a point P equals the angle F1 P F2, and the τ-coordinate equals the natural logarithm of the ratio of the distances d1 and d2:
- [math]\displaystyle{ \tau = \ln \frac{d_1}{d_2}. }[/math]
If, in the Cartesian system, the foci are taken to lie at (−a, 0) and (a, 0), the coordinates of the point P are
- [math]\displaystyle{ x = a \ \frac{\sinh \tau}{\cosh \tau - \cos \sigma}, \qquad y = a \ \frac{\sin \sigma}{\cosh \tau - \cos \sigma}. }[/math]
The coordinate τ ranges from [math]\displaystyle{ -\infty }[/math] (for points close to F1) to [math]\displaystyle{ \infty }[/math] (for points close to F2). The coordinate σ is only defined modulo 2π, and is best taken to range from -π to π, by taking it as the negative of the acute angle F1 P F2 if P is in the lower half plane.
Proof that coordinate system is orthogonal
The equations for x and y can be combined to give
or
- [math]\displaystyle{ x + i y = a \coth\left( \frac{\tau-i\sigma}{2}\right). }[/math]
This equation shows that σ and τ are the real and imaginary parts of an analytic function of x+iy (with logarithmic branch points at the foci), which in turn proves (by appeal to the general theory of conformal mapping) (the Cauchy-Riemann equations) that these particular curves of σ and τ intersect at right angles, i.e., it is an orthogonal coordinate system.
Curves of constant [math]\displaystyle{ \sigma }[/math] and [math]\displaystyle{ \tau }[/math]
The curves of constant σ correspond to non-concentric circles
-
[math]\displaystyle{ x^2 + \left( y - a \cot \sigma \right)^2 = \frac{a^{2}}{\sin^2 \sigma} = a^2(1+\cot^2\sigma) }[/math]
(1)
that intersect at the two foci. The centers of the constant-σ circles lie on the y-axis at [math]\displaystyle{ a\cot \sigma }[/math] with radius [math]\displaystyle{ \tfrac{a}{\sin\sigma} }[/math]. Circles of positive σ are centered above the x-axis, whereas those of negative σ lie below the axis. As the magnitude |σ|- π/2 decreases, the radius of the circles decreases and the center approaches the origin (0, 0), which is reached when |σ| = π/2. (From elementary geometry, all triangles on a circle with 2 vertices on opposite ends of a diameter are right triangles.)
The curves of constant [math]\displaystyle{ \tau }[/math] are non-intersecting circles of different radii
-
[math]\displaystyle{ \left( x - a \coth \tau \right)^2 + y^2 = \frac{a^2}{\sinh^2 \tau} = a^2(\coth^2\tau-1) }[/math]
(2)
that surround the foci but again are not concentric. The centers of the constant-τ circles lie on the x-axis at [math]\displaystyle{ a \coth\tau }[/math] with radius [math]\displaystyle{ \tfrac{a}{\sinh\tau} }[/math]. The circles of positive τ lie in the right-hand side of the plane (x > 0), whereas the circles of negative τ lie in the left-hand side of the plane (x < 0). The τ = 0 curve corresponds to the y-axis (x = 0). As the magnitude of τ increases, the radius of the circles decreases and their centers approach the foci.
Inverse relations
The passage from the Cartesian coordinates towards the bipolar coordinates can be done via the following formulas:
- [math]\displaystyle{ \tau = \frac{1}{2} \ln \frac{(x + a)^2 + y^2}{(x - a)^2 + y^2} }[/math]
and
- [math]\displaystyle{ \pi - \sigma = 2 \arctan \frac{2ay}{a^2 - x^2 - y^2 + \sqrt{(a^2 - x^2 - y^2)^2 + 4 a^2 y^2} }. }[/math]
The coordinates also have the identities:
- [math]\displaystyle{ \tanh \tau = \frac{2 a x}{x^2 + y^2 + a^2} }[/math]
and
- [math]\displaystyle{ \tan \sigma = \frac{2 a y}{x^2 + y^2 - a^2}, }[/math]
which can derived by solving Eq. (1) and (2) for [math]\displaystyle{ \cot \sigma }[/math] and [math]\displaystyle{ \coth\tau }[/math], respectively.
Scale factors
To obtain the scale factors for bipolar coordinates, we take the differential of the equation for [math]\displaystyle{ x + iy }[/math], which gives
- [math]\displaystyle{ dx + i\, dy = \frac{-ia}{\sin^2\bigl(\tfrac{1}{2}(\sigma + i \tau)\bigr)}(d\sigma +i\,d\tau). }[/math]
Multiplying this equation with its complex conjugate yields
- [math]\displaystyle{ (dx)^2 + (dy)^2 = \frac{a^2}{\bigl[2\sin\tfrac{1}{2}\bigl(\sigma + i\tau\bigr) \sin\tfrac{1}{2}\bigl(\sigma - i\tau\bigr)\bigr]^2} \bigl((d\sigma)^2 + (d\tau)^2\bigr). }[/math]
Employing the trigonometric identities for products of sines and cosines, we obtain
- [math]\displaystyle{ 2\sin\tfrac{1}{2}\bigl(\sigma + i\tau\bigr) \sin\tfrac{1}{2}\bigl(\sigma - i\tau\bigr) = \cos\sigma - \cosh\tau, }[/math]
from which it follows that
- [math]\displaystyle{ (dx)^2 + (dy)^2 = \frac{a^2}{(\cosh \tau - \cos\sigma)^2} \bigl((d\sigma)^2 + (d\tau)^2\bigr). }[/math]
Hence the scale factors for σ and τ are equal, and given by
- [math]\displaystyle{ h_\sigma = h_\tau = \frac{a}{\cosh \tau - \cos\sigma}. }[/math]
Many results now follow in quick succession from the general formulae for orthogonal coordinates. Thus, the infinitesimal area element equals
- [math]\displaystyle{ dA = \frac{a^2}{\left( \cosh \tau - \cos\sigma \right)^2} \, d\sigma\, d\tau, }[/math]
and the Laplacian is given by
- [math]\displaystyle{ \nabla^2 \Phi = \frac{1}{a^2} \left( \cosh \tau - \cos\sigma \right)^2 \left( \frac{\partial^2 \Phi}{\partial \sigma^2} + \frac{\partial^2 \Phi}{\partial \tau^2} \right). }[/math]
Expressions for [math]\displaystyle{ \nabla f }[/math], [math]\displaystyle{ \nabla \cdot \mathbf{F} }[/math], and [math]\displaystyle{ \nabla \times \mathbf{F} }[/math] can be expressed obtained by substituting the scale factors into the general formulae found in orthogonal coordinates.
Applications
The classic applications of bipolar coordinates are in solving partial differential equations, e.g., Laplace's equation or the Helmholtz equation, for which bipolar coordinates allow a separation of variables. An example is the electric field surrounding two parallel cylindrical conductors with unequal diameters.
Extension to 3-dimensions
Bipolar coordinates form the basis for several sets of three-dimensional orthogonal coordinates.
- The bipolar cylindrical coordinates are produced by translating the bipolar coordinates along the z-axis, i.e., the out-of-plane axis.
- The bispherical coordinates are produced by rotating the bipolar coordinates about the x-axis, i.e., the axis connecting the foci.
- The toroidal coordinates are produced by rotating the bipolar coordinates about the y-axis, i.e., the axis separating the foci.
See also
External links
- Interactive demo with desmos https://www.desmos.com/calculator/nbvnucu4o5
References
- ↑ Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999 "Bipolar Coordinates". http://bbs.sachina.pku.edu.cn/Stat/Math_World/math/b/b233.htm.
- ↑ Polyanin, Andrei Dmitrievich (2002). Handbook of linear partial differential equations for engineers and scientists. CRC Press. p. 476. ISBN 1-58488-299-9. https://books.google.com/books?id=NLnwhsevQGEC&pg=PA476.
- ↑ Happel, John; Brenner, Howard (1983). Low Reynolds number hydrodynamics: with special applications to particulate media. Mechanics of fluids and transport processes. 1. Springer. p. 497. ISBN 978-90-247-2877-0. https://books.google.com/books?id=tWO2xJZbweIC&pg=PA497.
- Hazewinkel, Michiel, ed. (2001), "Bipolar coordinates", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/b016470
- Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill.
 |