Two-center bipolar coordinates
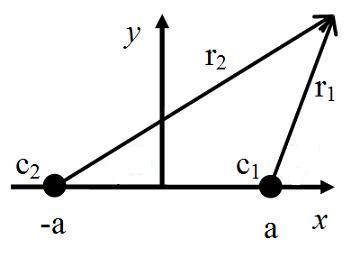
In mathematics, two-center bipolar coordinates is a coordinate system based on two coordinates which give distances from two fixed centers [math]\displaystyle{ c_1 }[/math] and [math]\displaystyle{ c_2 }[/math].[1] This system is very useful in some scientific applications (e.g. calculating the electric field of a dipole on a plane).[2][3]
Transformation to Cartesian coordinates
When the centers are at [math]\displaystyle{ (+a, 0) }[/math] and [math]\displaystyle{ (-a, 0) }[/math], the transformation to Cartesian coordinates [math]\displaystyle{ (x, y) }[/math] from two-center bipolar coordinates [math]\displaystyle{ (r_1, r_2) }[/math] is
- [math]\displaystyle{ x = \frac{r_2^2-r_1^2}{4a} }[/math]
- [math]\displaystyle{ y = \pm \frac{1}{4a}\sqrt{16a^2r_2^2-(r_2^2-r_1^2+4a^2)^2} }[/math][1]
Transformation to polar coordinates
When x > 0, the transformation to polar coordinates from two-center bipolar coordinates is
- [math]\displaystyle{ r = \sqrt{\frac{r_1^2+r_2^2-2a^2}{2}} }[/math]
- [math]\displaystyle{ \theta = \arctan\left( \frac{\sqrt{r_1^4-8a^2r_1^2-2r_1^2r_2^2-(4a^2-r_2^2)^2}}{r_2^2-r_1^2} \right) }[/math]
where [math]\displaystyle{ 2 a }[/math] is the distance between the poles (coordinate system centers).
Applications
Polar plotters use two-center bipolar coordinates to describe the drawing paths required to draw a target image.
See also
- Bipolar coordinates
- Biangular coordinates
- Lemniscate of Bernoulli
- Oval of Cassini
- Cartesian oval
- Ellipse
References
- ↑ 1.0 1.1 Weisstein, Eric W.. "Bipolar coordinates". http://mathworld.wolfram.com/BipolarCoordinates.html.
- ↑ R. Price, The Periodic Standing Wave Approximation: Adapted coordinates and spectral methods.
- ↑ The periodic standing-wave approximation: nonlinear scalar fields, adapted coordinates, and the eigenspectral method.
 |  |
