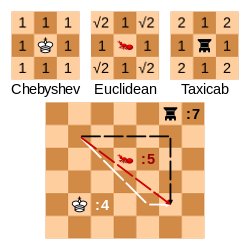
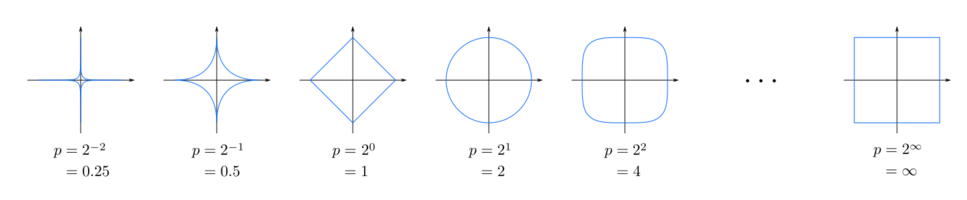Minkowski distance
This article does not cite any external source. HandWiki requires at least one external source. See citing external sources. (February 2023) (Learn how and when to remove this template message) |
The Minkowski distance or Minkowski metric is a metric in a normed vector space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance. It is named after the German mathematician Hermann Minkowski.
Definition
The Minkowski distance of order [math]\displaystyle{ p }[/math] (where [math]\displaystyle{ p }[/math] is an integer) between two points [math]\displaystyle{ X = (x_1,x_2,\ldots,x_n) \text{ and } Y = (y_1,y_2,\ldots,y_n) \in \R^n }[/math] is defined as: [math]\displaystyle{ D\left(X,Y\right) = \biggl(\sum_{i=1}^n |x_i-y_i|^p\biggr)^{\frac{1}{p}}. }[/math]
For [math]\displaystyle{ p \geq 1, }[/math] the Minkowski distance is a metric as a result of the Minkowski inequality. When [math]\displaystyle{ p \lt 1, }[/math] the distance between [math]\displaystyle{ (0, 0) }[/math] and [math]\displaystyle{ (1, 1) }[/math] is [math]\displaystyle{ 2^{1/p} \gt 2, }[/math] but the point [math]\displaystyle{ (0, 1) }[/math] is at a distance [math]\displaystyle{ 1 }[/math] from both of these points. Since this violates the triangle inequality, for [math]\displaystyle{ p \lt 1 }[/math] it is not a metric. However, a metric can be obtained for these values by simply removing the exponent of [math]\displaystyle{ 1/p. }[/math] The resulting metric is also an F-norm.
Minkowski distance is typically used with [math]\displaystyle{ p }[/math] being 1 or 2, which correspond to the Manhattan distance and the Euclidean distance, respectively. In the limiting case of [math]\displaystyle{ p }[/math] reaching infinity, we obtain the Chebyshev distance: [math]\displaystyle{ \lim_{p \to \infty}{\biggl(\sum_{i=1}^n |x_i-y_i|^p\biggr)^\frac{1}{p}} = \max_{i=1}^n |x_i-y_i|. }[/math]
Similarly, for [math]\displaystyle{ p }[/math] reaching negative infinity, we have: [math]\displaystyle{ \lim_{p \to -\infty}{\biggl(\sum_{i=1}^n |x_i-y_i|^p\biggr)^\frac{1}{p}} = \min_{i=1}^n |x_i-y_i|. }[/math]
The Minkowski distance can also be viewed as a multiple of the power mean of the component-wise differences between [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q. }[/math]
The following figure shows unit circles (the level set of the distance function where all points are at the unit distance from the center) with various values of [math]\displaystyle{ p }[/math]:
See also
- Generalized mean – N-th root of the arithmetic mean of the given numbers raised to the power n
- [math]\displaystyle{ L^p }[/math] space – Function spaces generalizing finite-dimensional p norm spaces
- Norm (mathematics) – Length in a vector space
External links
- Unit Balls for Different p-Norms in 2D and 3D at wolfram.com
- Unit-Norm Vectors under Different p-Norms at wolfram.com
- Simple IEEE 754 implementation in C++
- NPM JavaScript Package/Module
 |