Orthoptic (geometry)
In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.
Examples:
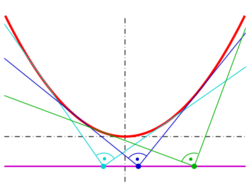
- The orthoptic of a parabola is its directrix (proof: see below),
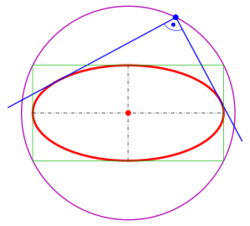
- The orthoptic of an ellipse [math]\displaystyle{ \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1 }[/math] is the director circle [math]\displaystyle{ x^2 + y^2 = a^2 + b^2 }[/math] (see below),
- The orthoptic of a hyperbola [math]\displaystyle{ \tfrac{x^2}{a^2} - \tfrac{y^2}{b^2} = 1,\ a \gt b }[/math] is the director circle [math]\displaystyle{ x^2 + y^2 = a^2 - b^2 }[/math] (in case of a ≤ b there are no orthogonal tangents, see below),
- The orthoptic of an astroid [math]\displaystyle{ x^{2/3} + y^{2/3} = 1 }[/math] is a quadrifolium with the polar equation [math]\displaystyle{ r=\tfrac{1}{\sqrt{2}}\cos(2\varphi), \ 0\le \varphi \lt 2\pi }[/math] (see below).
Generalizations:
- An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (see below).
- An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.
- Thales' theorem on a chord PQ can be considered as the orthoptic of two circles which are degenerated to the two points P and Q.
Orthoptic of a parabola
Any parabola can be transformed by a rigid motion (angles are not changed) into a parabola with equation [math]\displaystyle{ y = ax^2 }[/math]. The slope at a point of the parabola is [math]\displaystyle{ m = 2ax }[/math]. Replacing x gives the parametric representation of the parabola with the tangent slope as parameter: [math]\displaystyle{ \left(\tfrac{m}{2a},\tfrac{m^2}{4a} \right) \! . }[/math] The tangent has the equation [math]\displaystyle{ y=mx+n }[/math] with the still unknown n, which can be determined by inserting the coordinates of the parabola point. One gets [math]\displaystyle{ y=mx-\tfrac{m^2}{4a}\; . }[/math]
If a tangent contains the point (x0, y0), off the parabola, then the equation [math]\displaystyle{ y_0 = m x_0 -\frac{m^2}{4a} \quad \rightarrow \quad m^2 - 4ax_0\,m + 4ay_0 = 0 }[/math] holds, which has two solutions m1 and m2 corresponding to the two tangents passing (x0, y0). The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at (x0, y0) orthogonally, the following equations hold: [math]\displaystyle{ m_1 m_2 = -1 = 4 a y_0 }[/math] The last equation is equivalent to [math]\displaystyle{ y_0 = -\frac{1}{4a}\, , }[/math] which is the equation of the directrix.
Orthoptic of an ellipse and hyperbola
Ellipse
Let [math]\displaystyle{ E:\; \tfrac{x^2}{a^2} + \tfrac{y^2}{b^2} = 1 }[/math] be the ellipse of consideration.
- The tangents to the ellipse [math]\displaystyle{ E }[/math] at the vertices and co-vertices intersect at the 4 points [math]\displaystyle{ (\pm a, \pm b) }[/math], which lie on the desired orthoptic curve (the circle [math]\displaystyle{ x^2+y^2 = a^2 + b^2 }[/math]).
- The tangent at a point [math]\displaystyle{ (u,v) }[/math] of the ellipse [math]\displaystyle{ E }[/math] has the equation [math]\displaystyle{ \tfrac{u}{a^2} x + \tfrac{v}{b^2} y = 1 }[/math] (see tangent to an ellipse). If the point is not a vertex this equation can be solved for y: [math]\displaystyle{ y = -\tfrac{b^2u}{a^2v}\;x\; + \;\tfrac{b^2}{v}\, . }[/math]
Using the abbreviations
[math]\displaystyle{ \begin{align} m &= -\tfrac{b^2u}{a^2v},\\ \color{red}n &= \color{red}\tfrac{b^2}{v} \end{align} }[/math] |
|
() |
and the equation [math]\displaystyle{ {\color{blue}\tfrac{u^2}{a^2} = 1 - \tfrac{v^2}{b^2} = 1-\tfrac{b^2}{n^2}} }[/math] one gets: [math]\displaystyle{ m^2 = \frac{b^4 u^2}{a^4 v^2} = \frac{1}{a^2} {\color{red}\frac{b^4}{v^2}} {\color{blue}\frac{u^2}{a^2}} = \frac{1}{a^2} {\color{red}n^2} {\color{blue}\left(1-\frac{b^2}{n^2}\right)} = \frac{n^2-b^2}{a^2}\, . }[/math] Hence
[math]\displaystyle{ n = \pm\sqrt{m^2 a^2 + b^2} }[/math] |
|
() |
and the equation of a non vertical tangent is [math]\displaystyle{ y = m x \pm \sqrt{m^2 a^2 + b^2}. }[/math] Solving relations (I) for [math]\displaystyle{ u,v }[/math] and respecting (II) leads to the slope depending parametric representation of the ellipse: [math]\displaystyle{ (u,v) = \left(-\tfrac{ma^2}{\pm\sqrt{m^2a^2+b^2}}\;,\;\tfrac{b^2}{\pm\sqrt{m^2a^2+b^2}}\right)\, . }[/math] (For another proof: see Ellipse § Parametric representation.)
If a tangent contains the point [math]\displaystyle{ (x_0,y_0) }[/math], off the ellipse, then the equation [math]\displaystyle{ y_0 = m x_0 \pm \sqrt{m^2a^2+b^2} }[/math] holds. Eliminating the square root leads to [math]\displaystyle{ m^2 - \frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0, }[/math] which has two solutions [math]\displaystyle{ m_1,m_2 }[/math] corresponding to the two tangents passing through [math]\displaystyle{ (x_0,y_0) }[/math]. The constant term of a monic quadratic equation is always the product of its solutions. Hence, if the tangents meet at [math]\displaystyle{ (x_0,y_0) }[/math] orthogonally, the following equations hold:
[math]\displaystyle{ m_1 m_2 = -1 = \frac{y_0^2 - b^2}{x_0^2 - a^2} }[/math] The last equation is equivalent to [math]\displaystyle{ x_0^2+y_0^2 = a^2+b^2\, . }[/math] From (1) and (2) one gets:
Hyperbola
The ellipse case can be adopted nearly exactly to the hyperbola case. The only changes to be made are to replace [math]\displaystyle{ b^2 }[/math] with [math]\displaystyle{ -b^2 }[/math] and to restrict m to |m| > b/a. Therefore:
Orthoptic of an astroid
An astroid can be described by the parametric representation [math]\displaystyle{ \mathbf c(t) = \left(\cos^3t, \sin^3t\right), \quad 0 \le t \lt 2\pi. }[/math] From the condition [math]\displaystyle{ \mathbf \dot c(t) \cdot \mathbf \dot c(t+\alpha) = 0 }[/math] one recognizes the distance α in parameter space at which an orthogonal tangent to ċ(t) appears. It turns out that the distance is independent of parameter t, namely α = ± π/2. The equations of the (orthogonal) tangents at the points c(t) and c(t + π/2) are respectively: [math]\displaystyle{ \begin{align} y &= -\tan t \left(x-\cos^3 t\right) + \sin^3 t, \\ y &= \frac{1}{\tan t} \left(x+\sin^3 t\right) + \cos^3 t. \end{align} }[/math] Their common point has coordinates: [math]\displaystyle{ \begin{align} x &= \sin t \cos t \left(\sin t - \cos t\right), \\ y &= \sin t \cos t \left(\sin t + \cos t\right). \end{align} }[/math] This is simultaneously a parametric representation of the orthoptic.
Elimination of the parameter t yields the implicit representation [math]\displaystyle{ 2\left(x^2+y^2\right)^3 - \left(x^2-y^2\right)^2 = 0. }[/math] Introducing the new parameter φ = t − 5π/4 one gets [math]\displaystyle{ \begin{align} x &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\cos\varphi, \\ y &= \tfrac{1}{\sqrt{2}} \cos(2\varphi)\sin\varphi. \end{align} }[/math] (The proof uses the angle sum and difference identities.) Hence we get the polar representation [math]\displaystyle{ r = \tfrac{1}{\sqrt{2}} \cos(2\varphi), \quad 0 \le \varphi \lt 2\pi }[/math] of the orthoptic. Hence:
Isoptic of a parabola, an ellipse and a hyperbola
Below the isotopics for angles α ≠ 90° are listed. They are called α-isoptics. For the proofs see below.
Equations of the isoptics
- Parabola:
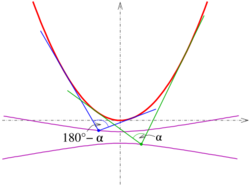
The α-isoptics of the parabola with equation y = ax2 are the branches of the hyperbola [math]\displaystyle{ x^2-\tan^2\alpha\left(y+\frac{1}{4a}\right)^2-\frac{y}{a}=0. }[/math] The branches of the hyperbola provide the isoptics for the two angles α and 180° − α (see picture).
- Ellipse:
The α-isoptics of the ellipse with equation x2/a2 + y2/b2 = 1 are the two parts of the degree-4 curve [math]\displaystyle{ \left(x^2+y^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y^2 + b^2x^2 - a^2b^2\right) }[/math] (see picture).
- Hyperbola:
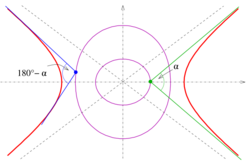
The α-isoptics of the hyperbola with the equation x2/a2 − y2/b2 = 1 are the two parts of the degree-4 curve [math]\displaystyle{ \left(x^2 + y^2 - a^2 + b^2\right)^2 \tan^2\alpha = 4 \left(a^2y^2 - b^2x^2 + a^2b^2\right). }[/math]
Proofs
- Parabola:
A parabola y = ax2 can be parametrized by the slope of its tangents m = 2ax: [math]\displaystyle{ \mathbf c(m) = \left(\frac{m}{2a},\frac{m^2}{4a}\right), \quad m \in \R. }[/math]
The tangent with slope m has the equation [math]\displaystyle{ y=mx-\frac{m^2}{4a}. }[/math]
The point (x0, y0) is on the tangent if and only if [math]\displaystyle{ y_0 = m x_0 - \frac{m^2}{4a}. }[/math]
This means the slopes m1, m2 of the two tangents containing (x0, y0) fulfil the quadratic equation [math]\displaystyle{ m^2 - 4ax_0m + 4ay_0 = 0. }[/math]
If the tangents meet at angle α or 180° − α, the equation [math]\displaystyle{ \tan^2\alpha = \left(\frac{m_1-m_2}{1+m_1 m_2}\right)^2 }[/math]
must be fulfilled. Solving the quadratic equation for m, and inserting m1, m2 into the last equation, one gets [math]\displaystyle{ x_0^2-\tan^2\alpha\left(y_0+\frac{1}{4a}\right)^2-\frac{y_0}{a} = 0. }[/math]
This is the equation of the hyperbola above. Its branches bear the two isoptics of the parabola for the two angles α and 180° − α.
- Ellipse:
In the case of an ellipse x2/a2 + y2/b2 = 1 one can adopt the idea for the orthoptic for the quadratic equation [math]\displaystyle{ m^2-\frac{2x_0y_0}{x_0^2-a^2}m + \frac{y_0^2-b^2}{x_0^2-a^2} = 0. }[/math]
Now, as in the case of a parabola, the quadratic equation has to be solved and the two solutions m1, m2 must be inserted into the equation [math]\displaystyle{ \tan^2\alpha=\left(\frac{m_1-m_2}{1+m_1m_2}\right)^2. }[/math]
Rearranging shows that the isoptics are parts of the degree-4 curve: [math]\displaystyle{ \left(x_0^2+y_0^2-a^2-b^2\right)^2 \tan^2\alpha = 4\left(a^2y_0^2+b^2x_0^2-a^2b^2\right). }[/math]
- Hyperbola:
The solution for the case of a hyperbola can be adopted from the ellipse case by replacing b2 with −b2 (as in the case of the orthoptics, see above).
To visualize the isoptics, see implicit curve.
External links
- Special Plane Curves.
- Mathworld
- Jan Wassenaar's Curves
- "Isoptic curve" at MathCurve
- "Orthoptic curve" at MathCurve
Notes
References
- Lawrence, J. Dennis (1972). A catalog of special plane curves. Dover Publications. pp. 58–59. ISBN 0-486-60288-5. https://archive.org/details/catalogofspecial00lawr/page/58.
- Odehnal, Boris (2010). "Equioptic Curves of Conic Sections". Journal for Geometry and Graphics 14 (1): 29–43. http://www.heldermann-verlag.de/jgg/jgg14/j14h1odeh.pdf.
- Schaal, Hermann (1977). Lineare Algebra und Analytische Geometrie. III. Vieweg. p. 220. ISBN 3-528-03058-5.
- Steiner, Jacob (1867). Vorlesungen über synthetische Geometrie. Leipzig: B. G. Teubner. Part 2, p. 186. https://archive.org/details/bub_gb_jCgPAAAAQAAJ.
- Ternullo, Maurizio (2009). "Two new sets of ellipse related concyclic points". Journal of Geometry 94 (1–2): 159–173. doi:10.1007/s00022-009-0005-7.
 |