Weierstrass function

Short description: Function that is continuous everywhere but differentiable nowhere

Plot of Weierstrass function over the interval [−2, 2]. Like some other fractals, the function exhibits self-similarity: every zoom (red circle) is similar to the global plot.

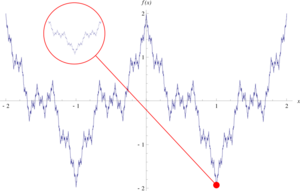
In mathematics, the Weierstrass function is an example of a real-valued function that is continuous everywhere but differentiable nowhere. It is an example of a fractal curve. It is named after its discoverer Karl Weierstrass.

The Weierstrass function has historically served the role of a pathological function, being the first published example (1872) specifically concocted to challenge the notion that every continuous function is differentiable except on a set of isolated points. Weierstrass's demonstration that continuity did not imply almost-everywhere differentiability upended mathematics, overturning several proofs that relied on geometric intuition and vague definitions of smoothness. These types of functions were denounced by contemporaries: Henri Poincaré famously described them as "monsters" and called Weierstrass' work "an outrage against common sense", while Charles Hermite wrote that they were a "lamentable scourge". The functions were difficult to visualize until the arrival of computers in the next century, and the results did not gain wide acceptance until practical applications such as models of Brownian motion necessitated infinitely jagged functions (nowadays known as fractal curves).

Construction

Animation based on the increasing of the b value from 0.1 to 5.

In Weierstrass's original paper, the function was defined as a Fourier series:

[math]\displaystyle{ f(x)=\sum_{n=0} ^\infty a^n \cos(b^n \pi x), }[/math]

where [math]\displaystyle{ 0\lt a\lt 1 }[/math], [math]\displaystyle{ b }[/math] is a positive odd integer, and

[math]\displaystyle{ ab \gt 1+\frac{3}{2} \pi. }[/math]

The minimum value of [math]\displaystyle{ b }[/math] for which there exists [math]\displaystyle{ 0\lt a\lt 1 }[/math] such that these constraints are satisfied is [math]\displaystyle{ b=7 }[/math]. This construction, along with the proof that the function is not differentiable over any interval, was first delivered by Weierstrass in a paper presented to the Königliche Akademie der Wissenschaften on 18 July 1872.

Despite being differentiable nowhere, the function is continuous: Since the terms of the infinite series which defines it are bounded by ±aⁿ and this has finite sum for 0 < a < 1, convergence of the sum of the terms is uniform by the Weierstrass M-test with M_n = aⁿ. Since each partial sum is continuous, by the uniform limit theorem, it follows that f is continuous. Additionally, since each partial sum is uniformly continuous, it follows that f is also uniformly continuous.

It might be expected that a continuous function must have a derivative, or that the set of points where it is not differentiable should be countably infinite or finite. According to Weierstrass in his paper, earlier mathematicians including Gauss had often assumed that this was true. This might be because it is difficult to draw or visualise a continuous function whose set of nondifferentiable points is something other than a countable set of points. Analogous results for better behaved classes of continuous functions do exist, for example the Lipschitz functions, whose set of non-differentiability points must be a Lebesgue null set (Rademacher's theorem). When we try to draw a general continuous function, we usually draw the graph of a function which is Lipschitz or otherwise well-behaved.

The Weierstrass function was one of the first fractals studied, although this term was not used until much later. The function has detail at every level, so zooming in on a piece of the curve does not show it getting progressively closer and closer to a straight line. Rather between any two points no matter how close, the function will not be monotone.

The computation of the Hausdorff dimension D of the graph of the classical Weierstrass function was an open problem until 2018, while it was generally believed that D = [math]\displaystyle{ 2 + \log_b(a) \lt 2 }[/math]. That D is strictly less than 2 follows from the conditions on [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] from above. Only after more than 30 years was this proved rigorously.

The term Weierstrass function is often used in real analysis to refer to any function with similar properties and construction to Weierstrass's original example. For example, the cosine function can be replaced in the infinite series by a piecewise linear "zigzag" function. G. H. Hardy showed that the function of the above construction is nowhere differentiable with the assumptions 0 < a < 1, ab ≥ 1.

Riemann function

The Weierstrass function is based on the earlier Riemann function, claimed to be differentiable nowhere. Occasionally, this function has also been called the Weierstrass function.

[math]\displaystyle{ f(x) = \sum_{n = 1}^\infty \frac{\sin(n^2x)}{n^2} }[/math]

While Bernhard Riemann strongly claimed that the function is differentiable nowhere, no evidence of this was published by Riemann, and Weierstrass noted that he did not find any evidence of it surviving either in Riemann's papers or orally from his students.

In 1916, G. H. Hardy confirmed that the function doesn't have a finite derivative in any value of [math]\displaystyle{ \pi x }[/math] where x is irrational or is rational with the form of either [math]\displaystyle{ \frac{2A}{4B+1} }[/math] or [math]\displaystyle{ \frac{2A+1}{2B} }[/math], where A and B are integers. In 1969, Joseph Gerver found that the Riemann function has a defined differential on every value of x that can be expressed in the form of [math]\displaystyle{ \frac{2A+1}{2B+1}\pi }[/math] with integer A and B, or rational multipliers of pi with an odd numerator and denominator. On these points, the function has a derivative of [math]\displaystyle{ -\frac{1}{2} }[/math]. In 1971, J. Gerver showed that the function has no finite differential at the values of x that can be expressed in the form of [math]\displaystyle{ \frac{2A}{2B+1}\pi }[/math], completing the problem of the differentiability of the Riemann function.

As the Riemann function is differentiable only on a null set of points, it is differentiable almost nowhere.

Hölder continuity

It is convenient to write the Weierstrass function equivalently as

[math]\displaystyle{ W_\alpha(x) = \sum_{n=0}^\infty b^{-n\alpha}\cos(b^n \pi x) }[/math]

for [math]\displaystyle{ \alpha = -\frac{\ln(a)}{\ln(b)} }[/math]. Then W_α(x) is Hölder continuous of exponent α, which is to say that there is a constant C such that

[math]\displaystyle{ |W_\alpha(x)-W_\alpha(y)|\le C|x-y|^\alpha }[/math]

for all x and y. Moreover, W₁ is Hölder continuous of all orders α < 1 but not Lipschitz continuous.

Density of nowhere-differentiable functions

It turns out that the Weierstrass function is far from being an isolated example: although it is "pathological", it is also "typical" of continuous functions:

• In a topological sense: the set of nowhere-differentiable real-valued functions on [0, 1] is comeager in the vector space C([0, 1]; R) of all continuous real-valued functions on [0, 1] with the topology of uniform convergence.
• In a measure-theoretic sense: when the space C([0, 1]; R) is equipped with classical Wiener measure γ, the collection of functions that are differentiable at even a single point of [0, 1] has γ-measure zero. The same is true even if one takes finite-dimensional "slices" of C([0, 1]; R), in the sense that the nowhere-differentiable functions form a prevalent subset of C([0, 1]; R).

See also

• Blancmange curve
• Koch snowflake
• Nowhere continuous function

References

• David, Claire (2018), "Bypassing dynamical systems : A simple way to get the box-counting dimension of the graph of the Weierstrass function", Proceedings of the International Geometry Center (Academy of Sciences of Ukraine) 11 (2): 53–68, doi:10.15673/tmgc.v11i2.1028 
• Falconer, K. (1984), The Geometry of Fractal Sets, Cambridge Tracts in Mathematics, Book 85, Cambridge: Cambridge University Press, ISBN 978-0-521-33705-2, https://books.google.com/books?id=-Kwp-GrimCIC 
• Gelbaum, B Bernard R.; Olmstead, John M. H. (2003), Counterexamples in Analysis, Dover Books on Mathematics, Dover Publications, ISBN 978-0-486-42875-8, https://books.google.com/books?id=D_XBAgAAQBAJ 
• Hardy, G. H. (1916), "Weierstrass's nondifferentiable function", Transactions of the American Mathematical Society (American Mathematical Society) 17 (3): 301–325, doi:10.2307/1989005, http://www.ams.org/journals/tran/1916-017-03/S0002-9947-1916-1501044-1/S0002-9947-1916-1501044-1.pdf 
• Weierstrass, Karl (18 July 1872), Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen, Königlich Preussische Akademie der Wissenschaften 
  • Weierstrass, Karl (1895), "Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen", Mathematische Werke von Karl Weierstrass, 2, Berlin, Germany: Mayer & Müller, pp. 71–74, https://books.google.com/books?id=1FhtAAAAMAAJ&pg=PA71 
  • English translation: Edgar, Gerald A. (1993), "On continuous functions of a real argument that do not possess a well-defined derivative for any value of their argument", Classics on Fractals, Studies in Nonlinearity, Addison-Wesley Publishing Company, pp. 3–9, ISBN 978-0-201-58701-2 

External links

• Weisstein, Eric W.. "Weierstrass function". http://mathworld.wolfram.com/WeierstrassFunction.html.  (a different Weierstrass Function which is also continuous and nowhere differentiable)
• Nowhere differentiable continuous function proof of existence using Banach's contraction principle.
• Nowhere monotonic continuous function proof of existence using the Baire category theorem.
• Johan Thim. "Continuous Nowhere Differentiable Functions". Master Thesis Lulea Univ of Technology 2003. http://epubl.ltu.se/1402-1617/2003/320/index-en.html. 
• Weierstrass function in the complex plane Beautiful fractal.
• SpringerLink - Journal of Fourier Analysis and Applications, Volume 16, Number 1 Simple Proofs of Nowhere-Differentiability for Weierstrass's Function and Cases of Slow Growth
• Weierstrass functions: continuous but not differentiable anywhere
• The Weierstrass Function by Brent Nelson at Berkeley, showing non differentiable