−1

Short description: Integer

Short description: Natural number

← −2 −1 0 →
-1 0 1 2 3 4 5 6 7 8 9 → List of numbers — Integers ← 0 10 20 30 40 50 60 70 80 90 →
Cardinal	−1, minus one, negative one
Ordinal	−1st (negative first)
Divisors	1
Arabic	−١
Chinese numeral	负一，负弌，负壹
Bengali	−১
Binary (byte)	S&M: 1000000012 2sC: 111111112
Hex (byte)	S&M: 0x10116 2sC: 0xFF16

In mathematics, −1 (negative one or minus one) is the additive inverse of 1, that is, the number that when added to 1 gives the additive identity element, 0. It is the negative integer greater than negative two (−2) and less than 0.

Algebraic properties

Multiplication

Further information: Additive inverse

Multiplying a number by −1 is equivalent to changing the sign of the number – that is, for any x we have (−1) ⋅ x = −x. This can be proved using the distributive law and the axiom that 1 is the multiplicative identity:

x + (−1) ⋅ x = 1 ⋅ x + (−1) ⋅ x = (1 + (−1)) ⋅ x = 0 ⋅ x = 0.

Here we have used the fact that any number x times 0 equals 0, which follows by cancellation from the equation

0 ⋅ x = (0 + 0) ⋅ x = 0 ⋅ x + 0 ⋅ x.

0, 1, −1, i, and −i in the complex or cartesian plane

In other words,

x + (−1) ⋅ x = 0,

so (−1) ⋅ x is the additive inverse of x, i.e. (−1) ⋅ x = −x, as was to be shown.

Square of −1

The square of −1, i.e. −1 multiplied by −1, equals 1. As a consequence, a product of two negative numbers is positive.

For an algebraic proof of this result, start with the equation

0 = −1 ⋅ 0 = −1 ⋅ [1 + (−1)].

The first equality follows from the above result, and the second follows from the definition of −1 as additive inverse of 1: it is precisely that number which when added to 1 gives 0. Now, using the distributive law, it can be seen that

0 = −1 ⋅ [1 + (−1)] = −1 ⋅ 1 + (−1) ⋅ (−1) = −1 + (−1) ⋅ (−1).

The third equality follows from the fact that 1 is a multiplicative identity. But now adding 1 to both sides of this last equation implies

(−1) ⋅ (−1) = 1.

The above arguments hold in any ring, a concept of abstract algebra generalizing integers and real numbers.

Square roots of −1

Although there are no real square roots of −1, the complex number i satisfies i² = −1, and as such can be considered as a square root of −1. The only other complex number whose square is −1 is −i because there are exactly two square roots of any non‐zero complex number, which follows from the fundamental theorem of algebra. In the algebra of quaternions – where the fundamental theorem does not apply – which contains the complex numbers, the equation x² = −1 has infinitely many solutions.

Inverse and invertible elements

The reciprocal function f(x) = x⁻¹ where for every x except 0, f(x) represents its multiplicative inverse

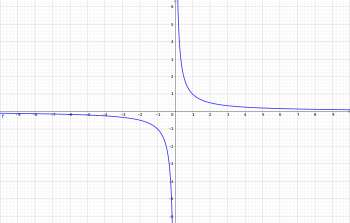
Exponentiation of a non‐zero real number can be extended to negative integers, where raising a number to the power −1 has the same effect as taking its multiplicative inverse:

x⁻¹ = 1/x.

This definition is then applied to negative integers, preserving the exponential law x^ax^b = x^{(a + b)} for real numbers a and b.

A −1 superscript in f ⁻¹(x) takes the inverse function of f(x), where ( f(x))⁻¹ specifically denotes a pointwise reciprocal. Where f is bijective specifying an output codomain of every y ∈ Y  from every input domain x ∈ X, there will be

f⁻¹( f(x)) = x,  and  f⁻¹( f(y)) = y.

When a subset of the codomain is specified inside the function f, its inverse will yield an inverse image, or preimage, of that subset under the function.

Rings

Exponentiation to negative integers can be further extended to invertible elements of a ring by defining x⁻¹ as the multiplicative inverse of x; in this context, these elements are considered units.

In a polynomial domain F [x] over any field F, the polynomial x has no inverse. If it did have an inverse q(x), then there would be

x q(x) = 1 ⇒ deg (x) + deg (q(x)) = deg (1)

                 ⇒ 1 + deg (q(x)) = 0

                 ⇒ deg (q(x)) = −1

which is not possible, and therefore, F [x] is not a field. More specifically, because the polynomial is not continuous, it is not a unit in F.

Uses

Sequences

Integer sequences commonly use −1 to represent an uncountable set, in place of "∞" as a value resulting from a given index.

As an example, the number of regular convex polytopes in n-dimensional space is,

{1, 1, −1, 5, 6, 3, 3, ...} for n = {0, 1, 2, ...} (sequence A060296 in the OEIS).

−1 can also be used as a null value, from an index that yields an empty set ∅ or non-integer where the general expression describing the sequence is not satisfied, or met.

For instance, the smallest k > 1 such that in the interval 1...k there are as many integers that have exactly twice n divisors as there are prime numbers is,

{2, 27, −1, 665, −1, 57675, −1, 57230, −1} for n = {1, 2, ..., 9} (sequence A356136 in the OEIS).

A non-integer or empty element is often represented by 0 as well.

Computing

In software development, −1 is a common initial value for integers and is also used to show that a variable contains no useful information.

See also

• Balanced ternary
• Menelaus's theorem