Astronomy:Axial precession
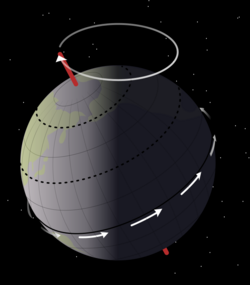
In astronomy, axial precession is a gravity-induced, slow, and continuous change in the orientation of an astronomical body's rotational axis. In the absence of precession, the astronomical body's orbit would show axial parallelism.[2] In particular, axial precession can refer to the gradual shift in the orientation of Earth's axis of rotation in a cycle of approximately 26,000 years.[1] This is similar to the precession of a spinning top, with the axis tracing out a pair of cones joined at their apices. The term "precession" typically refers only to this largest part of the motion; other changes in the alignment of Earth's axis—nutation and polar motion—are much smaller in magnitude.
Earth's precession was historically called the precession of the equinoxes, because the equinoxes moved westward along the ecliptic relative to the fixed stars, opposite to the yearly motion of the Sun along the ecliptic. Historically,[3] the discovery of the precession of the equinoxes is usually attributed in the West to the 2nd-century-BC astronomer Hipparchus. With improvements in the ability to calculate the gravitational force between planets during the first half of the nineteenth century, it was recognized that the ecliptic itself moved slightly, which was named planetary precession, as early as 1863, while the dominant component was named lunisolar precession.[4] Their combination was named general precession, instead of precession of the equinoxes.
Lunisolar precession is caused by the gravitational forces of the Moon and Sun on Earth's equatorial bulge, causing Earth's axis to move with respect to inertial space. Planetary precession (an advance) is due to the small angle between the gravitational force of the other planets on Earth and its orbital plane (the ecliptic), causing the plane of the ecliptic to shift slightly relative to inertial space. Lunisolar precession is about 500 times greater than planetary precession.[5] In addition to the Moon and Sun, the other planets also cause a small movement of Earth's axis in inertial space, making the contrast in the terms lunisolar versus planetary misleading, so in 2006 the International Astronomical Union recommended that the dominant component be renamed the precession of the equator, and the minor component be renamed precession of the ecliptic, but their combination is still named general precession.[6] Many references to the old terms exist in publications predating the change.
Nomenclature

"Precession" and "procession" are both terms that relate to motion. "Precession" is derived from the Latin praecedere ("to precede, to come before or earlier"), while "procession" is derived from the Latin procedere ("to march forward, to advance"). Generally the term "procession" is used to describe a group of objects moving forward. The stars viewed from Earth are seen to proceed from east to west daily, due to the Earth's diurnal motion, and yearly, due to the Earth's revolution around the Sun. At the same time the stars can be observed to anticipate slightly such motion, at the rate of approximately 50 arc seconds per year, a phenomenon known as the "precession of the equinoxes".
In describing this motion astronomers generally have shortened the term to simply "precession". In describing the cause of the motion physicists have also used the term "precession", which has led to some confusion between the observable phenomenon and its cause, which matters because in astronomy, some precessions are real and others are apparent. This issue is further obfuscated by the fact that many astronomers are physicists or astrophysicists.
The term "precession" used in astronomy generally describes the observable precession of the equinox (the stars moving retrograde across the sky), whereas the term "precession" as used in physics, generally describes a mechanical process.
Effects

The precession of the Earth's axis has a number of observable effects. First, the positions of the south and north celestial poles appear to move in circles against the space-fixed backdrop of stars, completing one circuit in approximately 26,000 years. Thus, while today the star Polaris lies approximately at the north celestial pole, this will change over time, and other stars will become the "north star".[3] In approximately 3,200 years, the star Gamma Cephei in the Cepheus constellation will succeed Polaris for this position. The south celestial pole currently lacks a bright star to mark its position, but over time precession also will cause bright stars to become South Stars. As the celestial poles shift, there is a corresponding gradual shift in the apparent orientation of the whole star field, as viewed from a particular position on Earth.
Secondly, the position of the Earth in its orbit around the Sun at the solstices, equinoxes, or other time defined relative to the seasons, slowly changes.[3] For example, suppose that the Earth's orbital position is marked at the summer solstice, when the Earth's axial tilt is pointing directly toward the Sun. One full orbit later, when the Sun has returned to the same apparent position relative to the background stars, the Earth's axial tilt is not now directly toward the Sun: because of the effects of precession, it is a little way "beyond" this. In other words, the solstice occurred a little earlier in the orbit. Thus, the tropical year, measuring the cycle of seasons (for example, the time from solstice to solstice, or equinox to equinox), is about 20 minutes shorter than the sidereal year, which is measured by the Sun's apparent position relative to the stars. After about 26 000 years the difference amounts to a full year, so the positions of the seasons relative to the orbit are "back where they started". (Other effects also slowly change the shape and orientation of the Earth's orbit, and these, in combination with precession, create various cycles of differing periods; see also Milankovitch cycles. The magnitude of the Earth's tilt, as opposed to merely its orientation, also changes slowly over time, but this effect is not attributed directly to precession.)
For identical reasons, the apparent position of the Sun relative to the backdrop of the stars at some seasonally fixed time slowly regresses a full 360° through all twelve traditional constellations of the zodiac, at the rate of about 50.3 seconds of arc per year, or 1 degree every 71.6 years.
At present, the rate of precession corresponds to a period of 25,772 years, so tropical year is shorter than sidereal year by 1,224.5 seconds (20 min 24.5 sec ≈ (365.24219 × 86400) / 25772).
The rate itself varies somewhat with time (see Values below), so one cannot say that in exactly 25,772 years the Earth's axis will be back to where it is now.
For further details, see Changing pole stars and Polar shift and equinoxes shift, below.
History
Hellenistic world
Hipparchus
The discovery of precession usually is attributed to Hipparchus (190–120 BC) of Rhodes or Nicaea, a Greek astronomer. According to Ptolemy's Almagest, Hipparchus measured the longitude of Spica and other bright stars. Comparing his measurements with data from his predecessors, Timocharis (320–260 BC) and Aristillus (~280 BC), he concluded that Spica had moved 2° relative to the autumnal equinox. He also compared the lengths of the tropical year (the time it takes the Sun to return to an equinox) and the sidereal year (the time it takes the Sun to return to a fixed star), and found a slight discrepancy. Hipparchus concluded that the equinoxes were moving ("precessing") through the zodiac, and that the rate of precession was not less than 1° in a century, in other words, completing a full cycle in no more than 36000 years.[7]
Virtually all of the writings of Hipparchus are lost, including his work on precession. They are mentioned by Ptolemy, who explains precession as the rotation of the celestial sphere around a motionless Earth. It is reasonable to presume that Hipparchus, similarly to Ptolemy, thought of precession in geocentric terms as a motion of the heavens, rather than of the Earth.
Ptolemy
The first astronomer known to have continued Hipparchus's work on precession is Ptolemy in the second century AD. Ptolemy measured the longitudes of Regulus, Spica, and other bright stars with a variation of Hipparchus's lunar method that did not require eclipses. Before sunset, he measured the longitudinal arc separating the Moon from the Sun. Then, after sunset, he measured the arc from the Moon to the star. He used Hipparchus's model to calculate the Sun's longitude, and made corrections for the Moon's motion and its parallax (Evans 1998, pp. 251–255). Ptolemy compared his own observations with those made by Hipparchus, Menelaus of Alexandria, Timocharis, and Agrippa. He found that between Hipparchus's time and his own (about 265 years), the stars had moved 2°40', or 1° in 100 years (36" per year; the rate accepted today is about 50" per year or 1° in 72 years). It is possible, however, that Ptolemy simply trusted Hipparchus' figure instead of making his own measurements. He also confirmed that precession affected all fixed stars, not just those near the ecliptic, and his cycle had the same period of 36,000 years as found by Hipparchus.[7]
Other authors
Most ancient authors did not mention precession and, perhaps, did not know of it. For instance, Proclus rejected precession, while Theon of Alexandria, a commentator on Ptolemy in the fourth century, accepted Ptolemy's explanation. Theon also reports an alternate theory:
- "According to certain opinions ancient astrologers believe that from a certain epoch the solstitial signs have a motion of 8° in the order of the signs, after which they go back the same amount. . . ." (Dreyer 1958, p. 204)
Instead of proceeding through the entire sequence of the zodiac, the equinoxes "trepidated" back and forth over an arc of 8°. The theory of trepidation is presented by Theon as an alternative to precession.
Alternative discovery theories
Babylonians
Various assertions have been made that other cultures discovered precession independently of Hipparchus. According to Al-Battani, the Chaldean astronomers had distinguished the tropical and sidereal year so that by approximately 330 BC, they would have been in a position to describe precession, if inaccurately, but such claims generally are regarded as unsupported.[8]
Maya
The archaeologist Susan Milbrath has speculated that the Mesoamerican Long Count calendar of "30,000 years involving the Pleiades...may have been an effort to calculate the precession of the equinox."[9] This view is held by few other professional scholars of Maya civilization.[citation needed]
Ancient Egyptians
Similar claims have been made that precession was known in Ancient Egypt during the dynastic era, prior to the time of Hipparchus (Ptolemaic period). However, these claims remain controversial. Some buildings in the Karnak temple complex, for instance, allegedly were oriented toward the point on the horizon where certain stars rose or set at key times of the year.[citation needed] Nonetheless, they kept accurate calendars and if they recorded the date of the temple reconstructions it would be a fairly simple matter to plot the rough precession rate. The Dendera Zodiac, a star-map from the Hathor temple at Dendera from a late (Ptolemaic) age, allegedly records precession of the equinoxes (Tompkins 1971). In any case, if the ancient Egyptians knew of precession, their knowledge is not recorded as such in any of their surviving astronomical texts.
Michael Rice wrote in his Egypt's Legacy, "Whether or not the ancients knew of the mechanics of the Precession before its definition by Hipparchos the Bithynian in the second century BC is uncertain, but as dedicated watchers of the night sky they could not fail to be aware of its effects." (p. 128) Rice believes that "the Precession is fundamental to an understanding of what powered the development of Egypt" (p. 10), to the extent that "in a sense Egypt as a nation-state and the king of Egypt as a living god are the products of the realisation by the Egyptians of the astronomical changes effected by the immense apparent movement of the heavenly bodies which the Precession implies." (p. 56). Rice says that "the evidence that the most refined astronomical observation was practised in Egypt in the third millennium BC (and probably even before that date) is clear from the precision with which the Pyramids at Giza are aligned to the cardinal points, a precision which could only have been achieved by their alignment with the stars. " (p. 31) The Egyptians also, says Rice, were "to alter the orientation of a temple when the star on whose position it had originally been set moved its position as a consequence of the Precession, something which seems to have happened several times during the New Kingdom." (p. 170)
India
Before 1200, India had two theories of trepidation, one with a rate and another without a rate, and several related models of precession. Each had minor changes or corrections by various commentators. The dominant of the three was the trepidation described by the most respected Indian astronomical treatise, the Surya Siddhanta (3:9–12), composed c. 400 but revised during the next few centuries. It used a sidereal epoch, or ayanamsa, that is still used by all Indian calendars, varying over the ecliptic longitude of 19°11′ to 23°51′, depending on the group consulted.[10] This epoch causes the roughly 30 Indian calendar years to begin 23–28 days after the modern vernal equinox. The vernal equinox of the Surya Siddhanta librated 27° in both directions from the sidereal epoch. Thus the equinox moved 54° in one direction and then back 54° in the other direction. This cycle took 7200 years to complete at a rate of 54″/year. The equinox coincided with the epoch at the beginning of the Kali Yuga in −3101 and again 3600 years later in 499. The direction changed from prograde to retrograde midway between these years at −1301 when it reached its maximum deviation of 27°, and would have remained retrograde, the same direction as modern precession, for 3600 years until 2299.[11][12]: 29–30
Another trepidation was described by Varāhamihira (c. 550). His trepidation consisted of an arc of 46°40′ in one direction and a return to the starting point. Half of this arc, 23°20′, was identified with the Sun's maximum declination on either side of the equator at the solstices. But no period was specified, thus no annual rate can be ascertained.[12]: 27–28
Several authors have described precession to be near 200,000 revolutions in a Kalpa of 4,320,000,000 years, which would be a rate of 200,000×360×3600/4,320,000,000 = 60″/year. They probably deviated from an even 200,000 revolutions to make the accumulated precession zero near 500. Visnucandra (c. 550–600) mentions 189,411 revolutions in a Kalpa or 56.8″/year. Bhaskara I (c. 600–680) mentions [1]94,110 revolutions in a Kalpa or 58.2″/year. Bhāskara II (c. 1150) mentions 199,699 revolutions in a Kalpa or 59.9″/year.[12]: 32–33
Chinese astronomy
Yu Xi (fourth century AD) was the first Chinese astronomer to mention precession. He estimated the rate of precession as 1° in 50 years (Pannekoek 1961, p. 92).
Middle Ages and Renaissance
In medieval Islamic astronomy, precession was known based on Ptolemy's Almagest, and by observations that refined the value.
Al-Battani, in his Zij Al-Sabi', after mentioning Hipparchus calculating precession, and Ptolemy's value of 1 degree per 100 solar years, says that he measured precession and found it to be one degree per 66 solar years.[13]
Subsequently, Al-Sufi mentions the same values in his Book of Fixed Stars, that Ptolemy's value for precession is 1 degree per 100 solar years. He then quotes a different value from Zij Al Mumtahan, which was done during Al-Ma'mun's reign, as 1 degree for every 66 solar years. He also quotes the aforementioned Al-Battani's Zij Al-Sabi' as adjusting coordinates for stars by 11 degrees and 10 minutes of arc to account for the difference between Al-Battani's time and Ptolemy's.[14]
Later, the Zij-i Ilkhani compiled at the Maragheh observatory sets the precession of the equinoxes at 51 arc seconds per annum, which is very close to the modern value of 50.2 arc seconds.[15]
In the Middle Ages, Islamic and Latin Christian astronomers treated "trepidation" as a motion of the fixed stars to be added to precession. This theory is commonly attributed to the Arab astronomer Thabit ibn Qurra, but the attribution has been contested in modern times. Nicolaus Copernicus published a different account of trepidation in De revolutionibus orbium coelestium (1543). This work makes the first definite reference to precession as the result of a motion of the Earth's axis. Copernicus characterized precession as the third motion of the Earth.[16]
Modern period
Over a century later precession was explained in Isaac Newton's Philosophiae Naturalis Principia Mathematica (1687), to be a consequence of gravitation (Evans 1998, p. 246). Newton's original precession equations did not work, however, and were revised considerably by Jean le Rond d'Alembert and subsequent scientists.
Hipparchus's discovery
Hipparchus gave an account of his discovery in On the Displacement of the Solsticial and Equinoctial Points (described in Almagest III.1 and VII.2). He measured the ecliptic longitude of the star Spica during lunar eclipses and found that it was about 6° west of the autumnal equinox. By comparing his own measurements with those of Timocharis of Alexandria (a contemporary of Euclid, who worked with Aristillus early in the 3rd century BC), he found that Spica's longitude had decreased by about 2° in the meantime (exact years are not mentioned in Almagest). Also in VII.2, Ptolemy gives more precise observations of two stars, including Spica and concludes that in each case a 2°:40' change occurred between 128 BC and AD 139 (hence, 1° per century or one full cycle in 36000 years, that is, the precessional period of Hipparchus as reported by Ptolemy; cf. page 328 in Toomer's translation of Almagest, 1998 edition)). He also noticed this motion in other stars. He speculated that only the stars near the zodiac shifted over time. Ptolemy called this his "first hypothesis" (Almagest VII.1), but did not report any later hypothesis Hipparchus might have devised. Hipparchus apparently limited his speculations, because he had only a few older observations, which were not very reliable.
Because the equinoctial points are not marked in the sky, Hipparchus needed the Moon as a reference point; he used a lunar eclipse to measure the position of a star. Hipparchus already had developed a way to calculate the longitude of the Sun at any moment. A lunar eclipse happens during Full moon, when the Moon is at opposition, precisely 180° from the Sun. Hipparchus is thought to have measured the longitudinal arc separating Spica from the Moon. To this value, he added the calculated longitude of the Sun, plus 180° for the longitude of the Moon. He did the same procedure with Timocharis' data (Evans 1998, p. 251). Observations such as these eclipses, incidentally, are the main source of data about when Hipparchus worked, since other biographical information about him is minimal. The lunar eclipses he observed, for instance, took place on 21 April 146 BC, and 21 March 135 BC (Toomer 1984, p. 135 n. 14).
Hipparchus also studied precession in On the Length of the Year. Two kinds of year are relevant to understanding his work. The tropical year is the length of time that the Sun, as viewed from the Earth, takes to return to the same position along the ecliptic (its path among the stars on the celestial sphere). The sidereal year is the length of time that the Sun takes to return to the same position with respect to the stars of the celestial sphere. Precession causes the stars to change their longitude slightly each year, so the sidereal year is longer than the tropical year. Using observations of the equinoxes and solstices, Hipparchus found that the length of the tropical year was 365+1/4−1/300 days, or 365.24667 days (Evans 1998, p. 209). Comparing this with the length of the sidereal year, he calculated that the rate of precession was not less than 1° in a century. From this information, it is possible to calculate that his value for the sidereal year was 365+1/4+1/144 days (Toomer 1978, p. 218). By giving a minimum rate, he may have been allowing for errors in observation.
To approximate his tropical year Hipparchus created his own lunisolar calendar by modifying those of Meton and Callippus in On Intercalary Months and Days (now lost), as described by Ptolemy in the Almagest III.1 (Toomer 1984, p. 139). The Babylonian calendar used a cycle of 235 lunar months in 19 years since 499 BC (with only three exceptions before 380 BC), but it did not use a specified number of days. The Metonic cycle (432 BC) assigned 6,940 days to these 19 years producing an average year of 365+1/4+1/76 or 365.26316 days. The Callippic cycle (330 BC) dropped one day from four Metonic cycles (76 years) for an average year of 365+1/4 or 365.25 days. Hipparchus dropped one more day from four Callippic cycles (304 years), creating the Hipparchic cycle with an average year of 365+1/4−1/304 or 365.24671 days, which was close to his tropical year of 365+1/4−1/300 or 365.24667 days.
Hipparchus's mathematical signatures are found in the Antikythera Mechanism, an ancient astronomical computer of the second century BC. The mechanism is based on a solar year, the Metonic Cycle, which is the period the Moon reappears in the same place in the sky with the same phase (full Moon appears at the same position in the sky approximately in 19 years), the Callipic cycle (which is four Metonic cycles and more accurate), the Saros cycle and the Exeligmos cycles (three Saros cycles for the accurate eclipse prediction). The study of the Antikythera Mechanism proves that the ancients have been using very accurate calendars based on all the aspects of solar and lunar motion in the sky. In fact, the Lunar Mechanism which is part of the Antikythera Mechanism depicts the motion of the Moon and its phase, for a given time, using a train of four gears with a pin and slot device which gives a variable lunar velocity that is very close to the second law of Kepler, i.e. it takes into account the fast motion of the Moon at perigee and slower motion at apogee. This discovery proves that Hipparchus mathematics were much more advanced than Ptolemy describes in his books, as it is evident that he developed a good approximation of Kepler's second law.
Changing pole stars
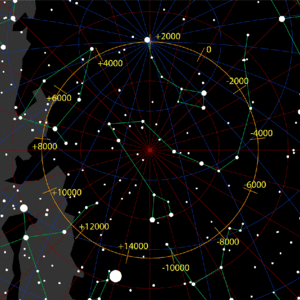
A consequence of the precession is a changing pole star. Currently Polaris is extremely well suited to mark the position of the north celestial pole, as Polaris is a moderately bright star with a visual magnitude of 2.1 (variable), and it is located about one degree from the pole, with no stars of similar brightness too close.[17]

The previous pole star was Kochab (Beta Ursae Minoris, β UMi, β Ursae Minoris), the brightest star in the bowl of the "Little Dipper", located 16 degrees from Polaris. It held that role from 1500 BC to AD 500.[18] It was not quite as accurate in its day as Polaris is today.[18] Today, Kochab and its neighbor Pherkad are referred to as the "Guardians of the Pole" (meaning Polaris).[18]
On the other hand, Thuban in the constellation Draco, which was the pole star in 3000 BC, is much less conspicuous at magnitude 3.67 (one-fifth as bright as Polaris); today it is invisible in light-polluted urban skies.
When Polaris becomes the north star again around 27,800, it will then be farther away from the pole than it is now due to its proper motion, while in 23,600 BC it came closer to the pole.
It is more difficult to find the south celestial pole in the sky at this moment, as that area is a particularly bland portion of the sky, and the nominal south pole star is Sigma Octantis, which with magnitude 5.5 is barely visible to the naked eye even under ideal conditions. That will change from the 80th to the 90th centuries, however, when the south celestial pole travels through the False Cross.
This situation also is seen on a star map. The orientation of the south pole is moving toward the Southern Cross constellation. For the last 2,000 years or so, the Southern Cross has pointed to the south celestial pole. As a consequence, the constellation is difficult to view from subtropical northern latitudes, unlike how it was in the time of the ancient Greeks. The Southern Cross can be viewed from as far north as Miami (about 25° N), but only during the winter/early spring.
Polar shift and equinoxes shift


The images at right attempt to explain the relation between the precession of the Earth's axis and the shift in the equinoxes. These images show the position of the Earth's axis on the celestial sphere, a fictitious sphere which places the stars according to their position as seen from Earth, regardless of their actual distance. The first image shows the celestial sphere from the outside, with the constellations in mirror image. The second image shows the perspective of a near-Earth position as seen through a very wide angle lens (from which the apparent distortion arises).
The rotation axis of the Earth describes, over a period of 25,700 years, a small blue circle among the stars near the top of the diagram, centered on the ecliptic north pole (the blue letter E) and with an angular radius of about 23.4°, an angle known as the obliquity of the ecliptic. The direction of precession is opposite to the daily rotation of the Earth on its axis. The brown axis was the Earth's rotation axis 5,000 years ago, when it pointed to the star Thuban. The yellow axis, pointing to Polaris, marks the axis now.
The equinoxes occur where the celestial equator intersects the ecliptic (red line), that is, where the Earth's axis is perpendicular to the line connecting the centers of the Sun and Earth. (The term "equinox" here refers to a point on the celestial sphere so defined, rather than the moment in time when the Sun is overhead at the Equator, though the two meanings are related.) When the axis precesses from one orientation to another, the equatorial plane of the Earth (indicated by the circular grid around the equator) moves. The celestial equator is just the Earth's equator projected onto the celestial sphere, so it moves as the Earth's equatorial plane moves, and the intersection with the ecliptic moves with it. The positions of the poles and equator on Earth do not change, only the orientation of the Earth against the fixed stars.
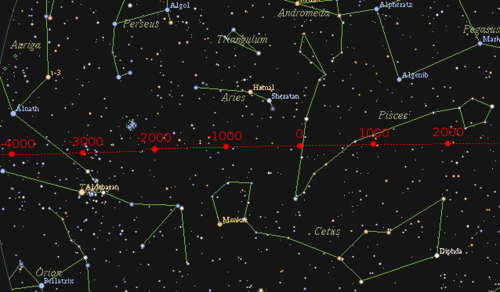
As seen from the brown grid, 5,000 years ago, the vernal equinox was close to the star Aldebaran in Taurus. Now, as seen from the yellow grid, it has shifted (indicated by the red arrow) to somewhere in the constellation of Pisces.
Still pictures like these are only first approximations, as they do not take into account the variable speed of the precession, the variable obliquity of the ecliptic, the planetary precession (which is a slow rotation of the ecliptic plane itself, presently around an axis located on the plane, with longitude 174.8764°) and the proper motions of the stars.
The precessional eras of each constellation, often known as "Great Months", are given, approximately, in the table below:[19]
| Constellation | Approximate year | |
|---|---|---|
| Entering | Exiting | |
| Taurus | 4500 BCE | 2000 BCE |
| Aries | 2000 BCE | 100 BCE |
| Pisces | 100 BCE | 2700 CE |
Cause
The precession of the equinoxes is caused by the gravitational forces of the Sun and the Moon, and to a lesser extent other bodies, on the Earth. It was first explained by Sir Isaac Newton.[20]
Axial precession is similar to the precession of a spinning top. In both cases, the applied force is due to gravity. For a spinning top, this force tends to be almost parallel to the rotation axis initially and increases as the top slows down. For a gyroscope on a stand it can approach 90 degrees. For the Earth, however, the applied forces of the Sun and the Moon are closer to perpendicular to the axis of rotation.
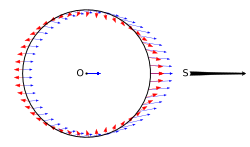
The Earth is not a perfect sphere but an oblate spheroid, with an equatorial diameter about 43 kilometers larger than its polar diameter. Because of the Earth's axial tilt, during most of the year the half of this bulge that is closest to the Sun is off-center, either to the north or to the south, and the far half is off-center on the opposite side. The gravitational pull on the closer half is stronger, since gravity decreases with the square of distance, so this creates a small torque on the Earth as the Sun pulls harder on one side of the Earth than the other. The axis of this torque is roughly perpendicular to the axis of the Earth's rotation so the axis of rotation precesses. If the Earth were a perfect sphere, there would be no precession.
This average torque is perpendicular to the direction in which the rotation axis is tilted away from the ecliptic pole, so that it does not change the axial tilt itself. The magnitude of the torque from the Sun (or the Moon) varies with the angle between the Earth's spin axis direction and that of the gravitational attraction. It approaches zero when they are perpendicular. For example, this happens at the equinoxes in the case of the interaction with the Sun. This can be seen to be since the near and far points are aligned with the gravitational attraction, so there is no torque due to the difference in gravitational attraction.
Although the above explanation involved the Sun, the same explanation holds true for any object moving around the Earth, along or close to the ecliptic, notably, the Moon. The combined action of the Sun and the Moon is called the lunisolar precession. In addition to the steady progressive motion (resulting in a full circle in about 25,700 years) the Sun and Moon also cause small periodic variations, due to their changing positions. These oscillations, in both precessional speed and axial tilt, are known as the nutation. The most important term has a period of 18.6 years and an amplitude of 9.2 arcseconds.[21]
In addition to lunisolar precession, the actions of the other planets of the Solar System cause the whole ecliptic to rotate slowly around an axis which has an ecliptic longitude of about 174° measured on the instantaneous ecliptic. This so-called planetary precession shift amounts to a rotation of the ecliptic plane of 0.47 seconds of arc per year (more than a hundred times smaller than lunisolar precession). The sum of the two precessions is known as the general precession.
Equations
The tidal force on Earth due to a perturbing body (Sun, Moon or planet) is expressed by Newton's law of universal gravitation, whereby the gravitational force of the perturbing body on the side of Earth nearest is said to be greater than the gravitational force on the far side by an amount proportional to the difference in the cubes of the distances between the near and far sides. If the gravitational force of the perturbing body acting on the mass of the Earth as a point mass at the center of Earth (which provides the centripetal force causing the orbital motion) is subtracted from the gravitational force of the perturbing body everywhere on the surface of Earth, what remains may be regarded as the tidal force. This gives the paradoxical notion of a force acting away from the satellite but in reality it is simply a lesser force toward that body due to the gradient in the gravitational field. For precession, this tidal force can be grouped into two forces which only act on the equatorial bulge outside of a mean spherical radius. This couple can be decomposed into two pairs of components, one pair parallel to Earth's equatorial plane toward and away from the perturbing body which cancel each other out, and another pair parallel to Earth's rotational axis, both toward the ecliptic plane.[22] The latter pair of forces creates the following torque vector on Earth's equatorial bulge:[5]
where
- GM, standard gravitational parameter of the perturbing body
- r, geocentric distance to the perturbing body
- C, moment of inertia around Earth's axis of rotation
- A, moment of inertia around any equatorial diameter of Earth
- C − A, moment of inertia of Earth's equatorial bulge (C > A)
- δ, declination of the perturbing body (north or south of equator)
- α, right ascension of the perturbing body (east from vernal equinox).
The three unit vectors of the torque at the center of the Earth (top to bottom) are x on a line within the ecliptic plane (the intersection of Earth's equatorial plane with the ecliptic plane) directed toward the vernal equinox, y on a line in the ecliptic plane directed toward the summer solstice (90° east of x), and z on a line directed toward the north pole of the ecliptic.
The value of the three sinusoidal terms in the direction of x (sinδ cosδ sinα) for the Sun is a sine squared waveform varying from zero at the equinoxes (0°, 180°) to 0.36495 at the solstices (90°, 270°). The value in the direction of y (sinδ cosδ (−cosα)) for the Sun is a sine wave varying from zero at the four equinoxes and solstices to ±0.19364 (slightly more than half of the sine squared peak) halfway between each equinox and solstice with peaks slightly skewed toward the equinoxes (43.37°(−), 136.63°(+), 223.37°(−), 316.63°(+)). Both solar waveforms have about the same peak-to-peak amplitude and the same period, half of a revolution or half of a year. The value in the direction of z is zero.
The average torque of the sine wave in the direction of y is zero for the Sun or Moon, so this component of the torque does not affect precession. The average torque of the sine squared waveform in the direction of x for the Sun or Moon is:
where
- , semimajor axis of Earth's (Sun's) orbit or Moon's orbit
- e, eccentricity of Earth's (Sun's) orbit or Moon's orbit
and 1/2 accounts for the average of the sine squared waveform, accounts for the average distance cubed of the Sun or Moon from Earth over the entire elliptical orbit,[23] and ε (the angle between the equatorial plane and the ecliptic plane) is the maximum value of δ for the Sun and the average maximum value for the Moon over an entire 18.6 year cycle.
Precession is:
where ω is Earth's angular velocity and Cω is Earth's angular momentum. Thus the first order component of precession due to the Sun is:[5]
whereas that due to the Moon is:
where i is the angle between the plane of the Moon's orbit and the ecliptic plane. In these two equations, the Sun's parameters are within square brackets labeled S, the Moon's parameters are within square brackets labeled L, and the Earth's parameters are within square brackets labeled E. The term accounts for the inclination of the Moon's orbit relative to the ecliptic. The term (C − A)/C is Earth's dynamical ellipticity or flattening, which is adjusted to the observed precession because Earth's internal structure is not known with sufficient detail. If Earth were homogeneous the term would equal its third eccentricity squared,[24]
where a is the equatorial radius (6378137 m) and c is the polar radius (6356752 m), so e2 = 0.003358481.
Applicable parameters for J2000.0 rounded to seven significant digits (excluding leading 1) are:[25][26]
| Sun | Moon | Earth |
|---|---|---|
| GM = 1.3271244×1020 m3/s2 | GM = 4.902799×1012 m3/s2 | (C − A)/C = 0.003273763 |
| a = 3.833978×108 m | a = 1.4959802×1011 m | |
| e = 0.05554553 | e = 0.016708634 | |
| i = 5.156690° | ε = 23.43928° | |
| ω = 7.292115×10−5 rad/s |
which yield
- dψS/dt = 2.450183×10−12 /s
- dψL/dt = 5.334529×10−12 /s
both of which must be converted to ″/a (arcseconds/annum) by the number of arcseconds in 2π radians (1.296×106″/2π) and the number of seconds in one annum (a Julian year) (3.15576×107s/a):
- dψS/dt = 15.948788″/a vs 15.948870″/a from Williams[5]
- dψL/dt = 34.723638″/a vs 34.457698″/a from Williams.
The solar equation is a good representation of precession due to the Sun because Earth's orbit is close to an ellipse, being only slightly perturbed by the other planets. The lunar equation is not as good a representation of precession due to the Moon because the Moon's orbit is greatly distorted by the Sun and neither the radius nor the eccentricity is constant over the year.
Values
Simon Newcomb's calculation at the end of the 19th century for general precession (p) in longitude gave a value of 5,025.64 arcseconds per tropical century, and was the generally accepted value until artificial satellites delivered more accurate observations and electronic computers allowed more elaborate models to be calculated. Jay Henry Lieske developed an updated theory in 1976, where p equals 5,029.0966 arcseconds (or 1.3969713 degrees) per Julian century. Modern techniques such as VLBI and LLR allowed further refinements, and the International Astronomical Union adopted a new constant value in 2000, and new computation methods and polynomial expressions in 2003 and 2006; the accumulated precession is:[27]
- pA = 5,028.796195 T + 1.1054348 T2 + higher order terms,
in arcseconds, with T, the time in Julian centuries (that is, 36,525 days) since the epoch of 2000.
The rate of precession is the derivative of that:
- p = 5,028.796195 + 2.2108696 T + higher order terms.
The constant term of this speed (5,028.796195 arcseconds per century in above equation) corresponds to one full precession circle in 25,771.57534 years (one full circle of 360 degrees divided by 50.28796195 arcseconds per year)[27] although some other sources put the value at 25771.4 years, leaving a small uncertainty.
The precession rate is not a constant, but is (at the moment) slowly increasing over time, as indicated by the linear (and higher order) terms in T. In any case it must be stressed that this formula is only valid over a limited time period. It is a polynomial expression centred on the J2000 datum, empirically fitted to observational data, not on a deterministic model of the Solar System. It is clear that if T gets large enough (far in the future or far in the past), the T² term will dominate and p will go to very large values. In reality, more elaborate calculations on the numerical model of the Solar System show that the precessional rate has a period of about 41,000 years, the same as the obliquity of the ecliptic. That is,
- p = A + BT + CT2 + …
is an approximation of
- p = a + b sin (2πT/P), where P is the 41,000-year period.
Theoretical models may calculate the constants (coefficients) corresponding to the higher powers of T, but since it is impossible for a polynomial to match a periodic function over all numbers, the difference in all such approximations will grow without bound as T increases. Sufficient accuracy can be obtained over a limited time span by fitting a high enough order polynomial to observation data, rather than a necessarily imperfect dynamic numerical model.[clarification needed] For present flight trajectory calculations of artificial satellites and spacecraft, the polynomial method gives better accuracy. In that respect, the International Astronomical Union has chosen the best-developed available theory. For up to a few centuries into the past and future, none of the formulas used diverge very much. For up to a few thousand years in the past and the future, most agree to some accuracy. For eras farther out, discrepancies become too large – the exact rate and period of precession may not be computed using these polynomials even for a single whole precession period.
The precession of Earth's axis is a very slow effect, but at the level of accuracy at which astronomers work, it does need to be taken into account on a daily basis. Although the precession and the tilt of Earth's axis (the obliquity of the ecliptic) are calculated from the same theory and are thus related one to the other, the two movements act independently of each other, moving in opposite directions.[clarification needed]
Precession rate exhibits a secular decrease due to tidal dissipation from 59"/a to 45"/a (a = annum = Julian year) during the 500 million year period centered on the present. After short-term fluctuations (tens of thousands of years) are averaged out, the long-term trend can be approximated by the following polynomials for negative and positive time from the present in "/a, where T is in billions of Julian years (Ga):[28]
- p− = 50.475838 − 26.368583 T + 21.890862 T2
- p+ = 50.475838 − 27.000654 T + 15.603265 T2
This gives an average cycle length now of 25,676 years.
Precession will be greater than p+ by the small amount of +0.135052"/a between +30 Ma and +130 Ma. The jump to this excess over p+ will occur in only 20 Ma beginning now because the secular decrease in precession is beginning to cross a resonance in Earth's orbit caused by the other planets.
According to Ward, when, in about 1,500 million years, the distance of the Moon, which is continuously increasing from tidal effects, has increased from the current 60.3 to approximately 66.5 Earth radii, resonances from planetary effects will push precession to 49,000 years at first, and then, when the Moon reaches 68 Earth radii in about 2,000 million years, to 69,000 years. This will be associated with wild swings in the obliquity of the ecliptic as well. Ward, however, used the abnormally large modern value for tidal dissipation. Using the 620-million year average provided by tidal rhythmites of about half the modern value, these resonances will not be reached until about 3,000 and 4,000 million years, respectively. However, due to the gradually increasing luminosity of the Sun, the oceans of the Earth will have vaporized before that time (about 2,100 million years from now).
See also
- Astronomical nutation
- Axial tilt
- Euler angles
- Longitude of vernal equinox
- Milankovitch cycles
- Polar motion
- Sidereal year
References
- ↑ 1.0 1.1 Hohenkerk, C.Y., Yallop, B.D., Smith, C.A., & Sinclair, A.T. "Celestial Reference Systems" in Seidelmann, P.K. (ed.) Explanatory Supplement to the Astronomical Almanac. Sausalito: University Science Books. p. 99.
- ↑ Lerner, K. Lee; Lerner, Brenda Wilmoth (2003). World of earth science. Farmington Hills, MI: Thomson-Gale. p. 105 and 454. ISBN 0-7876-9332-4. OCLC 60695883. "During revolution about the Sun, the earth's polar axis exhibits parallelism to Polaris (also known as the North Star). Although observing parallelism, the orientation of Earth's polar axis exhibits precession – a circular wobbling exhibited by gyroscopes – that results in a 28,000-year-long precessional cycle. Currently, Earth's polar axis points roughly in the direction of Polaris (the North Star). As a result of precession, over the next 11,000 years, Earth's axis will precess or wobble so that it assumes an orientation toward the star Vega."
- ↑ 3.0 3.1 3.2 Astro 101 – Precession of the Equinox , Western Washington University Planetarium. Retrieved 30 December 2008
- ↑ Robert Main, Practical and Spherical Astronomy (Cambridge: 1863) pp.203–4.
- ↑ 5.0 5.1 5.2 5.3 Williams, James G. (1994). "Contribution to the Earth's Obliquity Rate, Precession, and Nutation". The Astronomical Journal 108: 711. doi:10.1086/117108. Bibcode: 1994AJ....108..711W. https://articles.adsabs.harvard.edu/pdf/1994AJ....108..711W.
- ↑ "IAU 2006 Resolution B1: Adoption of the P03 Precession Theory and Definition of the Ecliptic". http://www.iau.org/static/resolutions/IAU2006_Resol1.pdf.
- ↑ 7.0 7.1 Ptolemy (1998), Ptolemy's Almagest, Princeton University Press, pp. 131–141, 321–340, ISBN 0-691-00260-6
- ↑ Neugebauer, O. (1950). "The Alleged Babylonian Discovery of the Precession of the Equinoxes". Journal of the American Oriental Society 70 (1): 1–8. doi:10.2307/595428.
- ↑ Susan Milbrath, "Just How Precise is Maya Astronomy?", Institute of Maya Studies newsletter, December 2007.
- ↑ Government of India (1955), Report of the Calendar Reform Committee, Council of Scientific and Industrial Research, p. 262, https://dspace.gipe.ac.in/xmlui/bitstream/handle/10973/39692/GIPE-043972.pdf, "The longitudes of the first point of Aries, according to the two schools therefore differ by 23°[51]′ (–) 19°11′ ... [Upper limit was increased by 42′ of accumulated precession 1950–2000.]"
- ↑ Surya (1935), Gangooly, Phanindralal, ed., Translation of Surya Siddhanta: A Textbook of Hindu Astronomy, University of Calcutta, pp. 114, https://archive.org/details/TranslationOfTheSuryaSiddhanta/page/n169
- ↑ 12.0 12.1 12.2 Pingree, David (1972), "Precession and trepidation in Indian astronomy before A.D. 1200", Journal for the History of Astronomy 3: 27–35, doi:10.1177/002182867200300104, Bibcode: 1972JHA.....3...27P
- ↑ Al-Battani. "Zij Al-Sabi'". http://shamela.ws/browse.php/book-452#page-132.
- ↑ Al-Sufi. "Book of Fixed Stars". https://www.wdl.org/ar/item/18412/view/1/20/.
- ↑ Rufus, W. C. (May 1939). "The Influence of Islamic Astronomy in Europe and the Far East". Popular Astronomy 47 (5): 233–238 [236]. Bibcode: 1939PA.....47..233R..
- ↑ Gillispie, Charles Coulston (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas. Princeton University Press. p. 24. ISBN 0-691-02350-6. https://archive.org/details/edgeofobjectivit00char.
- ↑ van Leeuwen, F. (2007). "HIP 11767". Hipparcos, the New Reduction. http://webviz.u-strasbg.fr/viz-bin/VizieR-5?-out.add=.&-source=I/311/hip2&recno=11739.
- ↑ 18.0 18.1 18.2 Benningfield, Damond (14 June 2015). "Kochab". Stardate Magazine (University of Texas McDonald Observatory). http://stardate.org/radio/program/2015-06-14.
- ↑ Kaler, James B. (2002). The Ever-Changing Sky: A guide to the celestial sphere (Reprint). Cambridge University Press. p. 152. ISBN 978-0521499187. https://books.google.com/books?id=KYLSMsduNqcC&pg=PA152.
- ↑ "precession of the equinoxes | Infoplease". https://www.infoplease.com/encyclopedia/science/space/astronomy/precession-of-the-equinoxes.
- ↑ "Basics of Space Flight, Chapter 2". Jet Propulsion Laboratory/NASA. 29 October 2013. http://www2.jpl.nasa.gov/basics/bsf2-1.php#nutation.
- ↑ Ivan I. Mueller, Spherical and practical astronomy as applied to geodesy (New York: Frederick Unger, 1969) 59.
- ↑ G. Boué & J. Laskar, "Precession of a planet with a satellite", Icarus 185 (2006) 312–330, p.329.
- ↑ George Biddel Airy, Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics (third edititon, 1842) 200.
- ↑ Simon, J. L.; Bretagnon, P.; Chapront, J.; Chapront-Touze, M.; Francou, G.; Laskar, J. (1994). "Numerical expressions for precession formulae and mean elements for the Moon and the planets". Astronomy and Astrophysics 282: 663. Bibcode: 1994A&A...282..663S.
- ↑ Dennis D. McCarthy, IERS Technical Note 13 – IERS Standards (1992) (Postscript, use XConvert).
- ↑ 27.0 27.1 N. Capitaine et al. 2003, p. 581 expression 39
- ↑ Laskar, J.; Robutel, P.; Joutel, F.; Gastineau, M.; Correia, A. C. M.; Levrard, B. (2004). "A long-term numerical solution for the insolation quantities of the Earth". Astronomy & Astrophysics 428: 261–285. doi:10.1051/0004-6361:20041335. Bibcode: 2004A&A...428..261L.
Bibliography
- Berger, A. L. (1976). "Obliquity and precession for the last 5000000 years". Astronomy and Astrophysics 51 (1): 127–135. Bibcode: 1976A&A....51..127B.
- Capitaine, N. (2003). "Expressions for IAU 2000 precession quantities". Astronomy & Astrophysics 412 (2): 567–586. doi:10.1051/0004-6361:20031539. Bibcode: 2003A&A...412..567C.
- Dreyer, J. L. E. A History of Astronomy from Thales to Kepler. 2nd ed. New York: Dover, 1953.
- Evans, James. The History and Practice of Ancient Astronomy. New York: Oxford University Press, 1998.
- Explanatory supplement to the Astronomical ephemeris and the American ephemeris and nautical almanac
- Hilton, J.L. (2006). "Report of the International Astronomical Union Division I Working Group on Precession and the Ecliptic". Celestial Mechanics and Dynamical Astronomy 94 (3): 351–367. doi:10.1007/s10569-006-0001-2. Bibcode: 2006CeMDA..94..351H. http://syrte.obspm.fr/iau2006/cm06_94_PEWG.pdf.
- Lieske, J. H.; Lederle, T.; Fricke, W. (1977). "Expressions for the Precession Quantities Based upon the IAU (1976) System of Astronomical Constants". Astron. Astrophys. 58: 1–16. Bibcode: 1977A&A....58....1L.
- Precession and the Obliquity of the Ecliptic has a comparison of values predicted by different theories
- Pannekoek, A. A History of Astronomy. New York: Dover, 1961.
- Parker, Richard A. "Egyptian Astronomy, Astrology, and Calendrical Reckoning." Dictionary of Scientific Biography 15:706–727.
- Rice, Michael (1997), Egypt's Legacy: The archetypes of Western civilization, 3000–30 BC, London and New York.
- Schütz, Michael (2000). "Hipparch und die Entdeckung der Präzession. Bemerkungen zu David Ulansey, Die Ursprünge des Mithraskultes" (in de). Electronic Journal of Mithraic Studies 1. http://www.uhu.es/ejms/Papers/Volume1Papers/ulansey.doc.
- Simon, J. L. (1994). "Numerical expressions for precession formulae and mean elements for the Moon and the planets". Astronomy and Astrophysics 282: 663–683. Bibcode: 1994A&A...282..663S.
- Tompkins, Peter. Secrets of the Great Pyramid. With an appendix by Livio Catullo Stecchini. New York: Harper Colophon Books, 1971.
- Toomer, G. J. "Hipparchus." Dictionary of Scientific Biography. Vol. 15:207–224. New York: Charles Scribner's Sons, 1978.
- Toomer, G. J. Ptolemy's Almagest. London: Duckworth, 1984.
- Ulansey, David. The Origins of the Mithraic Mysteries: Cosmology and Salvation in the Ancient World. New York: Oxford University Press, 1989.
- Vondrak, J.; Capitaine, N.; Wallace, P. (2011). "New precession expressions, valid for long time intervals". Astronomy & Astrophysics 534: A22. doi:10.1051/0004-6361/201117274. Bibcode: 2011A&A...534A..22V.
- Ward, W. R. (1982). "Comments on the long-term stability of the earth's obliquity". Icarus 50 (2–3): 444–448. doi:10.1016/0019-1035(82)90134-8. Bibcode: 1982Icar...50..444W.
External links
| Wikisource has the text of The New Student's Reference Work article "Precession". |
- D'Alembert and Euler's Debate on the Solution of the Precession of the Equinoxes
- Bowley, Roger; Merrifield, Michael. "Axial Precession". Sixty Symbols. Brady Haran for the University of Nottingham. http://www.sixtysymbols.com/videos/axial_precession.htm.
- Forced precession and nutation of Earth
 |

