Astronomy:Neutron-star oscillation

Short description: Extreme movement of neutron stars

Asteroseismology studies the internal structure of the Sun and other stars using oscillations. These can be studied by interpreting the temporal frequency spectrum acquired through observations. In the same way, the more extreme neutron stars might be studied and hopefully give us a better understanding of neutron-star interiors, and help in determining the equation of state for matter at nuclear densities. Scientists also hope to prove, or discard, the existence of so-called quark stars, or strange stars, through these studies. Fundamental information can be obtained of the General Relativity Theory by observing the gravitational radiation from oscillating neutron stars.

Comparison between predicted frequencies in a totally fluid, and in a three-component neutron-star model.
McDermott, P. N. (1985). "The nonradial oscillation spectra of neutron stars". The Astrophysical Journal 297: L37. doi:10.1086/184553. Bibcode: 1985ApJ...297L..37M. ; Reproduced by permission of the American Astronomical Society

Types of oscillations

The modes of oscillations are divided into subgroups, each with different characteristic behavior. First they are divided into toroidal and spherical modes, with the latter further divided into radial and non-radial modes. Spherical modes are oscillations in the radial direction while toroidal modes oscillate horizontally, perpendicular to the radial direction. The radial modes can be considered as a special case of non-radial ones, preserving the shape of the star in the oscillations, while the non-radial do not. Generally, only the spherical modes are considered in studies of stars, as they are the easiest to observe, but the toroidal modes might also be studied.

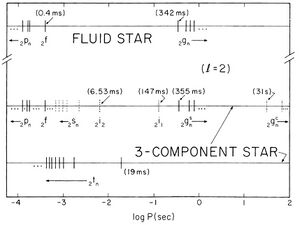
In the Sun, only three types of modes have been found so far, namely p-, g- and f- modes. Helioseismology studies these modes with periods in the range of minutes, while for neutron stars the periods are much shorter, often seconds or even milliseconds.

• p-modes or pressure modes, are determined by the local sound speed in the star, hence they are also often referred to as acoustic modes. Greatly dependent on the density and temperature of the neutron star, they are powered by internal pressure fluctuations in the stellar medium. Typical predicted periods lie around 0.1 ms.
• g-modes or gravity modes, have buoyancy as restoring force, but should not be confused with gravitational waves. The g-modes are confined to the inner regions of a neutron star with a solid crust, and have predicted oscillation periods between 10 and 400 ms. However, there are also expected long-period g-modes oscillating on periods longer than 10 s.
• f-modes or fundamental modes, are g-modes confined to the surface of the neutron star, similar to ripples in a pond. Predicted periods are between 0.1 and 0.8 ms.

The extreme properties of neutron stars permit several others types of modes.

• s-modes or shear modes, appear in two cases; one in the superfluid interior and one in the solid crust. In the crust they mainly depend on the crust's shear modulus. Predicted periods range between a few milliseconds to tens of seconds.
• i-modes or interfacial modes, appear at the boundaries of the different layers of the neutron star, causing traveling waves with periods dependent on the local density and temperature at the interface. Typical predicted periods lie around a few hundred milliseconds.
• t-modes or torsional modes, are caused by material motions tangentially to the surface in the crust. Predicted periods are shorter than 20 ms.
• r-modes or Rossby modes (a second type of toroidal mode) only appear in rotating stars and are caused by the Coriolis force acting as restoring force along the surface. Their periods are on the same order as the star's rotation. A phenomenological description could be found in [1]
• w-modes or gravitational-wave modes are a relativistic effect, dissipating energy through gravitational waves. Their existence was first suggested through a simple model problem by Kokkotas and Schutz and verified numerically by Kojima, whose results were corrected and extended by Kokkotas and Schutz. Characteristic properties of these modes are the absence of any significant fluid motion and their rapid damping times of tenths of seconds. There are three types of w-mode oscillations: curvature, trapped and interface modes, with predicted periods in the range of microseconds.
  • Trapped modes would exist in extremely compact stars. Their existence was suggested by Chandrasekhar and Ferrari, but so far no realistic Equation of State has been found allowing the formation of stars compact enough to support these modes.
  • Curvature modes exist in all relativistic stars and are related to the spacetime curvature. Models and numerical studies suggest an unlimited number of these modes.
  • Interface modes or wII-modes are somewhat similar to acoustic waves scattered off a hard sphere; there seems to be a finite number of these modes. They are rapidly damped in less than a tenth of a millisecond, and so would be hard to observe.

More details on stellar pulsation modes and a comparison with the pulsation modes of black holes can be found in the Living Review by Kokkotas and Schmidt.

Oscillation excitation

Generally, oscillations are caused when a system is perturbed from its dynamical equilibrium, and the system, using a restoration force, tries to return to that equilibrium state. The oscillations in neutron stars are probably weak with small amplitudes, but exciting these oscillations might increase the amplitudes to observable levels. One of the general excitation mechanisms are eagerly awaited outbursts, comparable to how one creates a tone when hitting a bell. The hit adds energy to the system, which excites the amplitudes of the oscillations to greater magnitude, and so is more easily observed. Apart from such outbursts, flares as they are often called, other mechanisms have been proposed to contribute to these excitations:

• The core collapse during a supernova which produces a neutron star is one good candidate as it releases enormous amounts of energy.
• For a binary system with at least one neutron star, the accretion process as matter flows into the star might be a source of moderately high energy.
• Gravitational radiation is released as the components in a binary systems spiral closer to each other, releasing energy which might be energetic enough for visible excitations.
• So called sudden phase transition (similar to water freezing) during transitions to, e.g., a strange star or a pion condensate. This releases energy which partly could be channeled to excitations.

Mode damping

The oscillations are damped through different processes in the neutron star which are not yet fully understood. The damping time is the time for the amplitude of a mode to decay to e⁻¹. A wide variety of different mechanisms have been found, but the strength of their impact differs among the modes.

• As the relative concentrations of protons, neutrons and electrons are altered, a small portion of energy will be carried away through neutrino emission. The damping times are very long as the light neutrinos cannot relieve much energy from the system.
• An oscillating magnetic field emits electromagnetic radiation with a power mainly dependent on that of the magnetic field. The mechanism is not very strong with damping times reaching days and even years.
• Gravitational radiation has been discussed a lot, with damping times believed to be on order of tenths of milliseconds.
• As the core and crust of a neutron star move against each other, there is internal friction which releases some smaller portion of energy. This mechanism has not been investigated thoroughly, but damping times are believed to be in the range of years.
• When the kinetic energy of the oscillations is converted into thermal energy in non-adiabatic effects, there is a possibility that significant energy might be released, although this mechanism is hard to investigate.

Observations

So far, most data about neutron-star oscillations come from the blasts of four specific Soft Gamma Repeaters, SGR, especially the event of 27 December 2004 from SGR 1806-20. Because so few events have been observed, little is known for sure about neutron stars and the physics of their oscillations. The outbursts which are vital for analyses only happen sporadically and are relatively brief. Given the limited knowledge, many of the equations surrounding the physics around these objects are parameterized to fit observed data, and where data is not to be found solar values are used instead. However, with more projects capable of observing these kinds of blasts with higher accuracy, and the hopeful development of w-mode studies, the future looks promising for better understanding one of the Universe's most exotic objects.

These oscilations can be observed through a gravitational wave observatories, like LISA. These kind of observations carry important information of the matter content of a neutron star, as well as fundamental information of the very nature of the spacetime itself.

See also

• Quasi-periodic oscillation

References

• Israel, G. L. (2005). "Discovery of rapid x-ray oscillations in the tail of the SGR 1806–20 hyperflare". The Astrophysical Journal 628 (1): L53–L56. doi:10.1086/432615. Bibcode: 2005ApJ...628L..53I. 
• Strohmayer, T. E.; Watts, A.L. (2005). "Discovery of fast x-ray oscillations during the 1998 giant flare from SGR 1900+14". The Astrophysical Journal 632 (2): L111–L114. doi:10.1086/497911. Bibcode: 2005ApJ...632L.111S. 
• Piro, A. L.; Bildsten, L. (2005). "Surface modes on bursting neutron stars and X-ray burst oscillations". The Astrophysical Journal 629 (1): 438–450. doi:10.1086/430777. Bibcode: 2005ApJ...629..438P. 
• Piro, A. L.; Bildsten, L. (2005). "Neutron star crustal interface waves". The Astrophysical Journal 619 (2): 1054–1063. doi:10.1086/426682. Bibcode: 2005ApJ...619.1054P. 

External links

• Asteroseismology of Sun-like Stars
• University of Vienna