Beltrami identity

Short description: Special case of the Euler-Lagrange equations

The Beltrami identity, named after Eugenio Beltrami, is a special case of the Euler–Lagrange equation in the calculus of variations.

The Euler–Lagrange equation serves to extremize action functionals of the form

[math]\displaystyle{ I[u]=\int_a^b L[x,u(x),u'(x)] \, dx \, , }[/math]

where [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] are constants and [math]\displaystyle{ u'(x) = \frac{du}{dx} }[/math].

If [math]\displaystyle{ \frac{\partial L}{\partial x} = 0 }[/math], then the Euler–Lagrange equation reduces to the Beltrami identity,

[math]\displaystyle{ L-u'\frac{\partial L}{\partial u'}=C \, , }[/math]

where C is a constant.

Derivation

By the chain rule, the derivative of L is

[math]\displaystyle{ \frac{dL}{dx} = \frac{\partial L}{\partial x} \frac{dx}{dx} + \frac{\partial L}{\partial u} \frac{du}{dx} + \frac{\partial L}{\partial u'} \frac{du'}{dx} \, . }[/math]

Because [math]\displaystyle{ \frac{\partial L}{\partial x} = 0 }[/math], we write

[math]\displaystyle{ \frac{dL}{dx} = \frac{\partial L}{\partial u} u' + \frac{\partial L}{\partial u'} u'' \, . }[/math]

We have an expression for [math]\displaystyle{ \frac{\partial L}{\partial u} }[/math] from the Euler–Lagrange equation,

[math]\displaystyle{ \frac{\partial L}{\partial u} = \frac{d}{dx} \frac{\partial L}{\partial u'} \, }[/math]

that we can substitute in the above expression for [math]\displaystyle{ \frac{dL}{dx} }[/math] to obtain

[math]\displaystyle{ \frac{dL}{dx} =u'\frac{d}{dx} \frac{\partial L}{\partial u'} + u''\frac{\partial L}{\partial u'} \, . }[/math]

By the product rule, the right side is equivalent to

[math]\displaystyle{ \frac{dL}{dx} = \frac{d}{dx} \left( u' \frac{\partial L}{\partial u'} \right) \, . }[/math]

By integrating both sides and putting both terms on one side, we get the Beltrami identity,

[math]\displaystyle{ L - u'\frac{\partial L}{\partial u'} = C \, . }[/math]

Applications

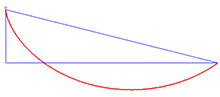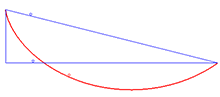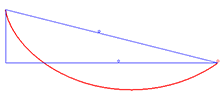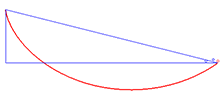
Solution to the brachistochrone problem

The solution to the brachistochrone problem is the cycloid.

An example of an application of the Beltrami identity is the brachistochrone problem, which involves finding the curve [math]\displaystyle{ y = y(x) }[/math] that minimizes the integral

[math]\displaystyle{ I[y] = \int_0^a \sqrt { {1+y'^{\, 2}} \over y } dx \, . }[/math]

The integrand

[math]\displaystyle{ L(y,y') = \sqrt{ {1+y'^{\, 2}} \over y } }[/math]

does not depend explicitly on the variable of integration [math]\displaystyle{ x }[/math], so the Beltrami identity applies,

[math]\displaystyle{ L-y'\frac{\partial L}{\partial y'}=C \, . }[/math]

Substituting for [math]\displaystyle{ L }[/math] and simplifying,

[math]\displaystyle{ y(1+y'^{\, 2}) = 1/C^2 ~~\text {(constant)} \, , }[/math]

which can be solved with the result put in the form of parametric equations

[math]\displaystyle{ x = A(\phi - \sin \phi) }[/math]

[math]\displaystyle{ y = A(1 - \cos \phi) }[/math]

with [math]\displaystyle{ A }[/math] being half the above constant, [math]\displaystyle{ \frac{1}{2C^{2}} }[/math], and [math]\displaystyle{ \phi }[/math] being a variable. These are the parametric equations for a cycloid.

Solution to the catenary problem

A chain hanging from points forms a catenary.

Consider a string with uniform density [math]\displaystyle{ \mu }[/math] of length [math]\displaystyle{ l }[/math] suspended from two points of equal height and at distance [math]\displaystyle{ D }[/math]. By the formula for arc length, [math]\displaystyle{ l = \int_S dS = \int_{s_1}^{s_2} \sqrt{1+y'^2}dx, }[/math] where [math]\displaystyle{ S }[/math] is the path of the string, and [math]\displaystyle{ s_1 }[/math] and [math]\displaystyle{ s_2 }[/math] are the boundary conditions.

The curve has to minimize its potential energy [math]\displaystyle{ U = \int_S g\mu y\cdot dS = \int_{s_1}^{s_2} g\mu y\sqrt{1+y'^2} dx, }[/math] and is subject to the constraint [math]\displaystyle{ \int_{s_1}^{s_2} \sqrt{1+y'^2} dx = l , }[/math] where [math]\displaystyle{ g }[/math] is the force of gravity.

Because the independent variable [math]\displaystyle{ x }[/math] does not appear in the integrand, the Beltrami identity may be used to express the path of the string as a separable first order differential equation

[math]\displaystyle{ L - \frac{\partial L}{\partial y\prime} = \mu gy\sqrt{1+y\prime ^2} + \lambda \sqrt{1+y\prime ^2} - \left[\mu gy\frac{y\prime ^2}{\sqrt{1+y\prime ^2}} + \lambda \frac{y\prime ^2}{\sqrt{1+y\prime ^2}}\right] = C, }[/math] where [math]\displaystyle{ \lambda }[/math] is the Lagrange multiplier.

It is possible to simplify the differential equation as such: [math]\displaystyle{ \frac{g\rho y - \lambda }{\sqrt{1+y'^2}} = C. }[/math]

Solving this equation gives the hyperbolic cosine, where [math]\displaystyle{ C_0 }[/math] is a second constant obtained from integration

[math]\displaystyle{ y = \frac{C}{\mu g}\cosh \left[ \frac{\mu g}{C} (x + C_0) \right] - \frac{\lambda}{\mu g}. }[/math]

The three unknowns [math]\displaystyle{ C }[/math], [math]\displaystyle{ C_0 }[/math], and [math]\displaystyle{ \lambda }[/math] can be solved for using the constraints for the string's endpoints and arc length [math]\displaystyle{ l }[/math], though a closed-form solution is often very difficult to obtain.