Biography:Anders Johan Lexell

Short description: Russian mathematician (1740–1784)

Anders Lexell
Silhouette by F. Anting (1784)
Born	(1740-12-24)24 December 1740 Åbo, Finland
Died	11 December 1784(1784-12-11) (aged 43) [OS: 30 November 1784] St. Petersburg, Russian Empire
Nationality	Swedish
Alma mater	The Royal Academy of Turku
Known for	Calculated the orbit of Lexell's Comet Calculated the orbit of Uranus
Scientific career
Fields	Mathematician Physicist Astronomer
Institutions	Uppsala Nautical School Imperial Russian Academy of Sciences
Doctoral advisor	Jakob Gadolin
Other academic advisors	M. J. Wallenius

Anders Johan Lexell (24 December 1740 – 11 December [O.S. 30 November] 1784) was a Finnish-Swedish astronomer, mathematician, and physicist who spent most of his life in Imperial Russia, where he was known as Andrei Ivanovich Leksel (Андрей Иванович Лексель).

Lexell made important discoveries in polygonometry and celestial mechanics; the latter led to a comet named in his honour. La Grande Encyclopédie states that he was the prominent mathematician of his time who contributed to spherical trigonometry with new and interesting solutions, which he took as a basis for his research of comet and planet motion. His name was given to a theorem of spherical triangles.

Lexell was one of the most prolific members of the Russian Academy of Sciences at that time, having published 66 papers in 16 years of his work there. A statement attributed to Leonhard Euler expresses high approval of Lexell's works: "Besides Lexell, such a paper could only be written by D'Alambert or me". Daniel Bernoulli also praised his work, writing in a letter to Johann Euler "I like Lexell's works, they are profound and interesting, and the value of them is increased even more because of his modesty, which adorns great men".

Lexell was unmarried, and kept up a close friendship with Leonhard Euler and his family. He witnessed Euler's death at his house and succeeded Euler to the chair of the mathematics department at the Russian Academy of Sciences, but died the following year. The asteroid 2004 Lexell is named in his honour, as is the lunar crater Lexell.

Life

Early years

Anders Johan Lexell was born in Turku to Johan Lexell, a goldsmith and local administrative officer, and Madeleine-Catherine née Björkegren. At the age of fourteen he enrolled at the Academy of Åbo and in 1760 received his Doctor of Philosophy degree with a dissertation Aphorismi mathematico-physici (academic advisor Jakob Gadolin). In 1763 Lexell moved to Uppsala and worked at Uppsala University as a mathematics lecturer. From 1766 he was a professor of mathematics at the Uppsala Nautical School.

St. Petersburg

In 1762, Catherine the Great ascended to the Russian throne and started the politics of enlightened absolutism. She was aware of the importance of science and ordered to offer Leonhard Euler to "state his conditions, as soon as he moves to St. Petersburg without delay". Soon after his return to Russia, Euler suggested that the director of the Russian Academy of Science should invite Lexell to study mathematics and its application to astronomy, especially spherical geometry. The invitation by Euler and the preparations that were made at that time to observe the 1769 transit of Venus from eight locations in the vast Russian Empire made Lexell seek the opportunity to become a member of the St. Petersburg scientific community.

To be admitted to the Russian Academy of Sciences, Lexell in 1768 wrote a paper on integral calculus called "Methodus integrandi nonnulis aequationum exemplis illustrata". Euler was appointed to evaluate the paper and highly praised it, and Count Vladimir Orlov, director of the Russian Academy of Sciences, invited Lexell to the position of mathematics adjunct, which Lexell accepted. In the same year he received permission from the Swedish king to leave Sweden, and moved to St. Petersburg.

His first task was to become familiar with the astronomical instruments that would be used in the observations of the transit of Venus. He participated in observing the 1769 transit at St. Petersburg together with Christian Mayer, who was hired by the Academy to work at the observatory while the Russian astronomers went to other locations.

Lexell made a large contribution to Lunar theory and especially to determining the parallax of the Sun from the results of observations of the transit of Venus. He earned universal recognition and, in 1771, when the Russian Academy of Sciences affiliated new members, Lexell was admitted as an Astronomy academician, he also became a member of the Academy of Stockholm and Academy of Uppsala in 1773 and 1774, and became a corresponding member of the Paris Royal Academy of Sciences.

Foreign trip

In 1775, the Swedish King appointed Lexell to a chair of the mathematics department at the University of Åbo with permission to stay at St. Petersburg for another three years to finish his work there; this permission was later prolonged for two more years. Hence, in 1780, Lexell was supposed to leave St. Petersburg and return to Sweden, which would have been a great loss for the Russian Academy of Sciences. Therefore, Director Domashnev proposed that Lexell travel to Germany, England, and France and then to return to St. Petersburg via Sweden. Lexell made the trip and, to the Academy's pleasure, got a discharge from the Swedish King and returned to St. Petersburg in 1781, after more than a year of absence, very satisfied with his trip.

Sending academicians abroad was quite rare at that time (as opposed to the early years of the Russian Academy of Sciences), so Lexell willingly agreed to make the trip. He was instructed to write his itinerary, which without changes was signed by Domashnev. The aims were as follows: since Lexell would visit major observatories on his way, he should learn how they were built, note the number and types of scientific instruments used, and if he found something new and interesting he should buy the plans and design drawings. He should also learn everything about cartography and try to get new geographic, hydrographic, military, and mineralogic maps. He should also write letters to the Academy regularly to report interesting news on science, arts, and literature.

Lexell departed St. Petersburg in late July 1780 on a sailing ship and via Swinemünde arrived in Berlin, where he stayed for a month and travelled to Potsdam, seeking in vain for an audience with King Frederick II. In September he left for Bavaria, visiting Leipzig, Göttingen, and Mannheim. In October he traveled to Straßbourg and then to Paris, where he spent the winter. In March 1781 he moved to London. In August he left London for Belgium, where he visited Flanders and Brabant, then moved to the Netherlands, visited The Hague, Amsterdam, and Saardam, and then returned to Germany in September. He visited Hamburg and then boarded a ship in Kiel to sail to Sweden; he spent three days in Kopenhagen on the way. In Sweden he spent time in his native city Åbo, and also visited Stockholm, Uppsala, and Åland. In early December 1781 Lexell returned to St. Petersburg, after having travelled for almost a year and a half.

There are 28 letters in the archive of the academy that Lexell wrote during the trip to Johann Euler, while the official reports that Euler wrote to the Director of the academy, Domashnev, were lost. However, unofficial letters to Johann Euler often contain detailed descriptions of places and people whom Lexell had met, and his impressions.

Last years

Lexell became very attached to Leonhard Euler, who lost his sight in his last years but continued working using his elder son Johann Euler to read for him. Lexell helped Leonhard Euler greatly, especially in applying mathematics to physics and astronomy. He helped Euler to write calculations and prepare papers. On 18 September 1783, after a lunch with his family, during a conversation with Lexell about the newly discovered Uranus and its orbit, Euler felt sick. He died a few hours later.

After Euler's passing, Academy Director, Princess Dashkova, appointed Lexell in 1783 Euler's successor. Lexell became a corresponding member of the Turin Royal Academy, and the London Board of Longitude put him on the list of scientists receiving its proceedings.

Lexell did not enjoy his position for long: he died on 30 November 1784.

Contribution to science

Lexell's theorem: the spherical triangles of constant area on a fixed base AB have their free vertex C along a small circle through the points antipodal to A and B.

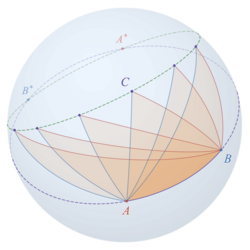
Lexell is mainly known for his works in astronomy and celestial mechanics, but he also worked in almost all areas of mathematics: algebra, differential calculus, integral calculus, geometry, analytic geometry, trigonometry, and continuum mechanics. Being a mathematician and working on the main problems of mathematics, he never missed the opportunity to look into specific problems in applied science, allowing for experimental proof of theory underlying the physical phenomenon. In 16 years of his work at the Russian Academy of Sciences, he published 62 works, and 4 more with coauthors, among whom are Leonhard Euler, Johann Euler, Wolfgang Ludwig Krafft, Stephan Rumovski, and Christian Mayer.

Differential equations

When applying for a position at the Russian Academy of Sciences, Lexell submitted a paper called "Method of analysing some differential equations, illustrated with examples", which was highly praised by Leonhard Euler in 1768. Lexell's method is as follows: for a given nonlinear differential equation (e.g. second order) we pick an intermediate integral—a first-order differential equation with undefined coefficients and exponents. After differentiating this intermediate integral we compare it with the original equation and get the equations for the coefficients and exponents of the intermediate integral. After we express the undetermined coefficients via the known coefficients we substitute them in the intermediate integral and get two particular solutions of the original equation. Subtracting one particular solution from another we get rid of the differentials and get a general solution, which we analyse at various values of constants. The method of reducing the order of the differential equation was known at that time, but in another form. Lexell's method was significant because it was applicable to a broad range of linear differential equations with constant coefficients that were important for physics applications. In the same year, Lexell published another article "On integrating the differential equation aⁿdⁿy + ba^n-1d^m-1ydx + ca^n-2d^m-2ydx² + ... + rydxⁿ = Xdxⁿ" presenting a general highly algorithmic method of solving higher order linear differential equations with constant coefficients.

Lexell also looked for criteria of integrability of differential equations. He tried to find criteria for the whole differential equations and also for separate differentials. In 1770 he derived a criterion for integrating differential function, proved it for any number of items, and found the integrability criteria for [math]\displaystyle{ dx\int{Vdx} }[/math], [math]\displaystyle{ dx\int{dx\int{Vdx}} }[/math], [math]\displaystyle{ dx\int{dx\int{dx\int{Vdx}}} }[/math]. His results agreed with those of Leonhard Euler but were more general and were derived without the means of calculus of variations. At Euler's request, in 1772 Lexell communicated these results to Lagrange and Lambert.

Concurrently with Euler, Lexell worked on expanding the integrating factor method to higher order differential equations. He developed the method of integrating differential equations with two or three variables by means of the integrating factor. He stated that his method could be expanded for the case of four variables: "The formulas will be more complicated, while the problems leading to such equations are rare in analysis".

Also of interest is the integration of differential equations in Lexell's paper "On reducing integral formulas to rectification of ellipses and hyperbolae", which discusses elliptic integrals and their classification, and in his paper "Integrating one differential formula with logarithms and circular functions", which was reprinted in the transactions of the Swedish Academy of Sciences. He also integrated a few complicated differential equations in his papers on continuum mechanics, including a four-order partial differential equation in a paper about coiling a flexible plate to a circular ring.

There is an unpublished Lexell paper in the archive of the Russian Academy of Sciences with the title "Methods of integration of some differential equations", in which a complete solution of the equation [math]\displaystyle{ x=y\phi(x')+\psi(x') }[/math], now known as the Lagrange–d'Alembert equation (ru), is presented.

Polygonometry

Polygonometry was a significant part of Lexell's work. He used the trigonometric approach using the advance in trigonometry made mainly by Euler and presented a general method of solving simple polygons in two articles "On solving rectilinear polygons". Lexell discussed two separate groups of problems: the first had the polygon defined by its sides and angles, the second with its diagonals and angles between diagonals and sides. For the problems of the first group Lexell derived two general formulas giving [math]\displaystyle{ n }[/math] equations allowing to solve a polygon with [math]\displaystyle{ n }[/math] sides. Using these theorems he derived explicit formulas for triangles and tetragons and also gave formulas for pentagons, hexagons, and heptagons. He also presented a classification of problems for tetragons, pentagons, and hexagons. For the second group of problems, Lexell showed that their solutions can be reduced to a few general rules and presented a classification of these problems, solving the corresponding combinatorial problems. In the second article he applied his general method for specific tetragons and showed how to apply his method to a polygon with any number of sides, taking a pentagon as an example.

The successor of Lexell's trigonometric approach (as opposed to a coordinate approach) was Swiss mathematician L'Huilier. Both L'Huilier and Lexell emphasized the importance of polygonometry for theoretical and practical applications.

Celestial mechanics and astronomy

File:Lexell - Disquisitio de investiganda vera quantitate parallaxeos solis ex transitus veneris ante discum solis anno 1769, 1772 - 726057 F.tif Lexell's first work at the Russian Academy of Sciences was to analyse data collected from the observation of the 1769 transit of Venus. He published four papers in "Novi Commentarii Academia Petropolitanae" and ended his work with a monograph on determining the parallax of the Sun, published in 1772.

Lexell aided Euler in finishing his Lunar theory, and was credited as a co-author in Euler's 1772 "Theoria motuum Lunae".

After that, Lexell spent most of his effort on comet astronomy (though his first paper on calculating the orbit of a comet is dated 1770). In the next ten years he calculated the orbits of all the newly discovered comets, among them the comet which Charles Messier discovered in 1770. Lexell calculated its orbit, showed that the comet had had a much larger perihelion before the encounter with Jupiter in 1767 and predicted that after encountering Jupiter again in 1779 it would be altogether expelled from the inner Solar System. This comet was later named Lexell's Comet.

Lexell also was the first to calculate the orbit of Uranus and to actually prove that it was a planet rather than a comet. He made preliminary calculations while travelling in Europe in 1781 based on Hershel's and Maskelyne's observations. Having returned to Russia, he estimated the orbit more precisely based on new observations, but due to the long orbital period it was still not enough data to prove that the orbit was not parabolic. Lexell then found the record of a star observed in 1759 by Christian Mayer in Pisces that was neither in the Flamsteed catalogues nor in the sky by the time Bode sought it. Lexell presumed that it was an earlier sighting of the same astronomical object and using this data he calculated the exact orbit, which proved to be elliptical, and proved that the new object was actually a planet. In addition to calculating the parameters of the orbit Lexell also estimated the planet's size more precisely than his contemporaries using Mars that was in the vicinity of the new planet at that time. Lexell also noticed that the orbit of Uranus was being perturbed. He then stated that, based on his data on various comets, the size of the Solar System can be 100 AU or even more, and that it could be other planets there that perturb the orbit of Uranus (although the position of the eventual Neptune was not calculated until much later by Urbain Le Verrier).

Further reading

• Stén, Johan C.-E. (2015): A Comet of the Enlightenment: Anders Johan Lexell's Life and Discoveries. Basel: Birkhäuser. ISBN:978-3-319-00617-8