Chemistry:Multipole density formalism

Isosurface of static electron density for doxycycline resulting from the Multipole Model refinement at [math]\displaystyle{ 1.5 \AA /e^3 }[/math] level.

Equivalent isosurface resulting from the Independent Atom Model. Notice the lack of covalent bonds' electrons.

The Multipole Density Formalism (also referred to as Hansen-Coppens Formalism) is an X-ray crystallography method of electron density modelling proposed by Niels K. Hansen and Philip Coppens in 1978. Unlike the commonly used Independent Atom Model, the Hansen-Coppens Formalism presents an aspherical approach, allowing one to model the electron distribution around a nucleus separately in different directions and therefore describe numerous chemical features of a molecule inside the unit cell of an examined crystal in detail.

Theory

Visual representations of a few real spherical harmonics used in Multipole Density Formalism. The distance of the surface from the origin is proportional to the value for given angles, while the color denotes the sign (blue for positive, yellow for negative).

Independent Atom Model

The Independent Atom Model (abbreviated to IAM), upon which the Multipole Model is based, is a method of charge density modelling. It relies on an assumption that electron distribution around the atom is isotropic, and that therefore charge density is dependent only on the distance from a nucleus. The choice of the radial function used to describe this electron density is arbitrary, granted that its value at the origin is finite. In practice either Gaussian- or Slater-type 1s-orbital functions are used.

Due to its simplistic approach, this method provides a straightforward model that requires no additional parameters (other than positional and Debye–Waller factors) to be refined. This allows the IAM to perform satisfactorily while a relatively low amount of data from the diffraction experiment is available. However, the fixed shape of the singular basis function prevents any detailed description of aspherical atomic features.

Kappa Formalism

In order to adjust some valence shell parameters, the Kappa formalism was proposed. It introduces two additional refineable parameters: an outer shell population (denoted as [math]\displaystyle{ P_{val} }[/math]) and its expansion/contraction ([math]\displaystyle{ \kappa }[/math]). Therefore, the electron density is formulated as:

[math]\displaystyle{ \rho_{atom} = \rho_{core} + \rho'_{valence}(\kappa r) = \rho_{core} + P_{val} \kappa^3 \rho_{val} (\kappa r) }[/math]

While [math]\displaystyle{ P_{val} }[/math], being responsible for the charge flow part, is linearly coupled with partial charge, the normalised [math]\displaystyle{ \kappa }[/math] parameter scales radial coordinate [math]\displaystyle{ r }[/math]. Therefore, lowering the [math]\displaystyle{ \kappa }[/math] parameter results in expansion of the outer shell and, conversely, raising it results in contraction. Although the Kappa formalism is still, strictly speaking, a spherical method, it is an important step towards understanding modern approaches as it allows one to distinguish chemically different atoms of the same element.

Multipole description

In the multipole model description, the charge density around a nucleus is given by the following equation:

[math]\displaystyle{ \rho_{atom}(r,\theta,\phi) = P_{core}\rho_{core}(r) + P_{val} \kappa^3 \rho_{val} (\kappa r) + \sum_{l=0}^{l_{max}}\kappa'^3 R_l (\kappa' r) \sum_{m=-l}^{l} P_{lm\pm}Y_{lm\pm}(\theta,\phi) }[/math]

The spherical part remains almost indistinguishable from the Kappa formalism, the only difference being one parameter corresponding to the population of the inner shell. The real strength of the Hansen-Coppens formalism lies in the right, deformational part of the equation. Here [math]\displaystyle{ \kappa' }[/math] fulfils a role similar to [math]\displaystyle{ \kappa }[/math] in the Kappa formalism (expansion/contraction of the aspherical part), whereas individual [math]\displaystyle{ R_l }[/math] are fixed spherical functions, analogous to [math]\displaystyle{ \rho }[/math]. Spherical harmonics [math]\displaystyle{ Y_{lm} }[/math] (each with its populational parameter [math]\displaystyle{ P_{lm} }[/math]) are, however, introduced to simulate the electrically anisotropic charge distribution.

In this approach, a fixed coordinate system for each atom needs to be applied. Although at first glance it seems practical to arbitrarily and indiscriminately make it contingent on the unit cell for all atoms present, it is far more beneficial to assign each atom its own local coordinates, which allows for focusing on hybridisation-specific interactions. While the singular sigma bond of the hydrogen can be described well using certain z-parallel pseudoorbitals, xy-plane oriented multipoles with a 3-fold rotational symmetry will prove more beneficial for flat aromatic structures.

Applications

Electron density isosurface map around a covalent bond modelled with the Multipole Model, with populational parameters taken from the ELMAM2 database. Note the elongated high-density area next to the hydrogen atom, pointing in the direction of oxygen.

Electron density isosurface map around a covalent bond modelled with the Independent Atom Model in the same scale. Nucleus-centred functions impose lower charge density on the bond path.

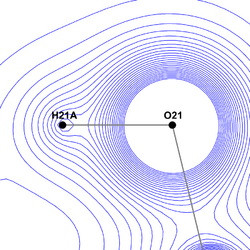
The primary advantage of the Hansen-Coppens formalism is its ability to free the model from spherical restraints and describe the surroundings of a nucleus far more accurately. In this way it becomes possible to examine some molecular features which would normally be only roughly approximated or completely ignored.

Hydrogen positioning

X-ray crystallography allows the researcher to precisely determine the position of peak electron density and to reason about the placement of nuclei based on this information. This approach works without any problems for heavy (non-hydrogen) atoms, whose inner shell electrons contribute to the density function to a far greater degree then outer shell electrons.

However, hydrogen atoms possess a feature unique among all the elements - they possess exactly one electron, which additionally is located on their valence shell and therefore is involved in creating strong covalent bonds with atoms of various other elements. While a bond is forming, the maximum of the electron density function moves significantly away from the nucleus and towards the other atom. This prevents any spherical approach from determining hydrogen position correctly by itself. Therefore, usually the hydrogen position is estimated basing on neutron crystallography data for similar molecules, or it is not modelled at all in the case of low-quality diffraction data.

It is possible (albeit disputable) to freely refine hydrogen atoms' positions using the Hansen-Coppens formalism, after releasing the bond lengths from any restraints derived from neutron measurements. The bonding orbital simulated with adequate multipoles describes the density distribution neatly while preserving believable bond lengths. It may be worth approximating hydrogen atoms' anisotropic displacement parameters, e.g. using SHADE, before introducing the formalism and, possibly, discarding bond distance constraints.

Bonding modelling

In order to analyse the length and strength of various interactions within the molecule, Richard Bader's "Atoms in molecules" theorem may be applied. Due to the complex description of the electron field provided by this aspherical model, it becomes possible to establish realistic bond paths between interacting atoms as well as to find and characterise their critical points. Deeper insight into this data yields useful information about bond strength, type, polarity or ellipticity, and when compared with other molecules brings greater understanding about the actual electron structure of the examined compound.

Charge flow

Due to the fact that for each multipole of every atom its population is being refined independently, individual charges will rarely be integers. In real cases, electron density flows freely through the molecule and is not bound by any restrictions resulting from the outdated Bohr atom model and found in IAM. Therefore, through e.g. an accurate Bader analysis, net atomic charges may be estimated, which again is beneficial for deepening the understanding of systems under investigation.

Drawbacks and limitations

Although the Multipole Formalism is a simple and straightforward alternative means of structure refinement, it is definitely not flawless. While usually for each atom either three or nine parameters are to be refined, depending on whether an anisotropic displacement is being taken into account or not, a full multipole description of heavy atoms belonging to the fourth and subsequent periods (such as chlorine, iron or bromine) requires refinement of up to 37 parameters. This proves problematic for any crystals possessing large asymmetric units (especially macromolecular compounds) and renders a refinement using the Hansen-Coppens Formalism unachievable for low-quality data with an unsatisfactory ratio of independent reflections to refined parameters.

Caution should be taken while refining some of the parameters simultaneously (i.e. [math]\displaystyle{ \kappa }[/math] or [math]\displaystyle{ \kappa' }[/math], multipole populations and thermal parameters), as they may correlate strongly, resulting in an unstable refinement or unphysical parameter values. Applying additional constraints resulting from local symmetry for each atom in a molecule (which decreases the number of refined multipoles) or importing populational parameters from existing databases may also be necessary to achieve a passable model. On the other hand, the aforementioned approaches significantly reduce the amount of information required from experiments, while preserving some level of detail concerning aspherical charge distribution. Therefore, even macromolecular structures with satisfactory X-ray diffraction data can be modelled aspherically in a similar fashion.

Despite their similarity, individual multipoles do not correspond to atomic projections of molecular orbitals of a wavefuntion as resulting from quantum calculations. Nevertheless, as brilliantly summarized by Stewart, "The structure of the model crystal density, as a superposition of pseudoatoms [...] does have quantitative features which are close to many results based on quantum chemical calculations". If the overlap between the atomic wavefunctions is small enough, as it occurs for example in transition metal complexes, the atomic multipoles may be correlated with the atomic valence orbitals and multipolar coefficients may be correlated with populations of metal d-orbitals. A stronger correlation between the X-ray measured diffracted intensities and quantum mechanical wavefunctions is possible using the wavefunction based methods of Quantum Crystallography, as for example the X-ray atomic orbital model, the so-called experimental wavefunction or the Hirshfeld Atom Refinement.