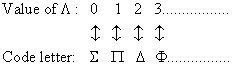Chemistry:Symmetry of diatomic molecules

Short description: Class of molecular symmetry

Molecular symmetry in physics and chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in the application of Quantum Mechanics in physics and chemistry, for example it can be used to predict or explain many of a molecule's properties, such as its dipole moment and its allowed spectroscopic transitions (based on selection rules), without doing the exact rigorous calculations (which, in some cases, may not even be possible). To do this it is necessary to classify the states of the molecule using the irreducible representations from the character table of the symmetry group of the molecule. Among all the molecular symmetries, diatomic molecules show some distinct features and they are relatively easier to analyze.

Symmetry and group theory

The physical laws governing a system is generally written as a relation (equations, differential equations, integral equations etc.). An operation on the ingredients of this relation, which keeps the form of the relations invariant is called a symmetry transformation or a symmetry of the system.

• These symmetry operations can involve external or internal co-ordinates; giving rise to geometrical or internal symmetries.
• These symmetry operations can be global or local; giving rise to global or gauge symmetries.
• These symmetry operations can be discrete or continuous.

Symmetry is a fundamentally important concept in quantum mechanics. It can predict conserved quantities and provide quantum numbers. It can predict degeneracies of eigenstates and gives insights about the matrix elements of the Hamiltonian without calculating them. Rather than looking into individual symmetries, it is sometimes more convenient to look into the general relations between the symmetries. It turns out that Group theory is the most efficient way of doing this.

Groups

A group is a mathematical structure (usually denoted in the form (G,*)) consisting of a set G and a binary operation [math]\displaystyle{ '*' }[/math] (sometimes loosely called 'multiplication'), satisfying the following properties:

1. closure: For every pair of elements [math]\displaystyle{ x,y\in G }[/math], the product [math]\displaystyle{ x*y\in G }[/math].
2. associativity: For every x and y and z in G, both (x*y)*z and x*(y*z) result with the same element in G  (in symbols, [math]\displaystyle{ (x*y)*z=x*(y*z)\forall x,y,z\in G }[/math]).
3. existence of identity: There must be an element (say e ) in G such that product any element of G with e make no change to the element (in symbols, [math]\displaystyle{ x*e=e*x=x;\forall x\in G }[/math] ).
4. existence of inverse: For each element ( x ) in G, there must be an element y in G such that product of x and y is the identity element e  (in symbols, for each [math]\displaystyle{ x\in G }[/math][math]\displaystyle{ \text{ }\exists \text{ }y\in G }[/math] such that [math]\displaystyle{ x*y=y*x=e }[/math]).

• In addition to the above four, if it so happens that [math]\displaystyle{ \forall x,y\in G }[/math],[math]\displaystyle{ x*y=y*x }[/math], i.e., the operation in commutative, then the group is called an abelian group. Otherwise it is called a non-abelian group.

Groups, symmetry and conservation

The set of all symmetry transformations of a Hamiltonian has the structure of a group, with group multiplication equivalent to applying the transformations one after the other. The group elements can be represented as matrices, so that the group operation becomes the ordinary matrix multiplication. In quantum mechanics, the evolution of an arbitrary superposition of states are given by unitary operators, so each of the elements of the symmetry groups are unitary operators. Now any unitary operator can be expressed as the exponential of some Hermitian operator. So, the corresponding Hermitian operators are the 'generators' of the symmetry group. These unitary transformations act on the Hamiltonian operator in some Hilbert space in a way that the Hamiltonian remains invariant under the transformations. In other words, the symmetry operators commute with the Hamiltonian. If [math]\displaystyle{ U }[/math] represents the unitary symmetry operator and acts on the Hamiltonian [math]\displaystyle{ H }[/math], then;

[math]\displaystyle{ [H,U]=0 }[/math]
[math]\displaystyle{ \begin{align} & {H}'={{U}^{\dagger }}HU=H \\ & \Rightarrow HU=UH \\ & \Rightarrow [H,U]=0;\forall U\in G \\ \end{align} }[/math]

These operators have the above-mentioned properties of a group:

• The symmetry operations are closed under multiplication.
• Application of symmetry transformations are associative.
• There is always a trivial transformation, where nothing is done to the original co-ordinates. This is the identity element of the group.
• And as long as an inverse transformation exists, it is a symmetry transformation, i.e. it leaves the Hamiltonian invariant. Thus the inverse is part of this set.

So, by the symmetry of a system, we mean a set of operators, each of which commutes with the Hamiltonian, and they form a symmetry group. This group may be abelian or non-abelian. Depending upon which one it is, the properties of the system changes (for example, if the group is abelian, there would be no degeneracy). Corresponding to every different kind of symmetry in a system, we can find a symmetry group associated with it.

It follows that the generator [math]\displaystyle{ T }[/math] of the symmetry group also commutes with the Hamiltonian. Now, it follows that:

The observable corresponding to the generator Hermitian matrix, is conserved.

The derivative of the expectation value of the operator T can be written as: [math]\displaystyle{ \frac{d\left\langle T \right\rangle }{dt}=\frac{d\left\langle \Psi |T|\Psi \right\rangle }{dt}=\left\langle \frac{\partial \Psi }{\partial t}|T|\Psi \right\rangle +\left\langle \Psi |\frac{\partial T}{\partial t}|\Psi \right\rangle +\left\langle \Psi |T|\frac{\partial \Psi }{\partial t} \right\rangle }[/math] Now, [math]\displaystyle{ i\hbar \frac{\partial \left| \Psi \right\rangle }{\partial t}=H\left| \Psi \right\rangle }[/math] So, [math]\displaystyle{ \frac{d\left\langle T \right\rangle }{dt}=-\frac{1}{i\hbar }\left\langle \Psi |HT|\Psi \right\rangle +\frac{1}{i\hbar }\left\langle \Psi |TH|\Psi \right\rangle +\left\langle \frac{\partial T}{\partial t} \right\rangle }[/math] as H is also Hermitian. So we have, [math]\displaystyle{ \frac{d\left\langle T \right\rangle }{dt}=\frac{1}{i\hbar }\left\langle [H,T] \right\rangle +\left\langle \frac{\partial T}{\partial t} \right\rangle }[/math] Now, [math]\displaystyle{ [H,T]=0 }[/math] as stated above, and if the operator T does not have any explicit time-dependence; [math]\displaystyle{ \frac{d\left\langle T \right\rangle }{dt}=0 }[/math] [math]\displaystyle{ \Rightarrow \left\langle T \right\rangle }[/math] is a constant, independent of what the state [math]\displaystyle{ \left| \Psi \right\rangle }[/math] may be. So the observable corresponding to the operator T, is conserved.

Some specific examples can be systems having rotational, translational invariance etc. For a rotationally invariant system, the symmetry group of the Hamiltonian is the general rotation group. Now, if (say) the system is invariant about any rotation about Z-axis (i.e., the system has axial symmetry), then the symmetry group of the Hamiltonian is the group of rotation about the symmetry axis. Now, this group is generated by the Z-component of the orbital angular momentum, [math]\displaystyle{ {{L}}_{{z}} }[/math] (general group element [math]\displaystyle{ R(\alpha)={{e}^{\frac{-i\alpha {{L}_{z}}}{\hbar }}} }[/math]). Thus, [math]\displaystyle{ {{L}}_{{z}} }[/math] commutes with [math]\displaystyle{ H }[/math] for this system and Z-component of the angular momentum is conserved. Similarly, translation symmetry gives rise to conservation of linear momentum, inversion symmetry gives rise to parity conservation and so on.

Geometrical symmetries

Symmetry operations, point groups and permutation-inversion groups

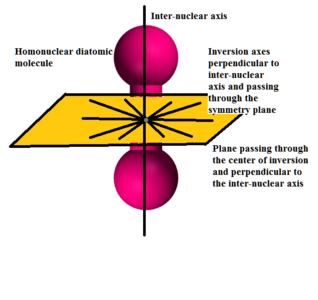
A molecule at equilibrium in a certain electronic state usually has some geometrical symmetry. This symmetry is described by a certain point group which consists of operations (called symmetry operations) that produce a spatial orientation of the molecule that is indistinguishable from the starting configuration. There are five types of point group symmetry operation: identity, rotation, reflection, inversion and improper rotation or rotation-reflection. Common to all symmetry operations is that the geometrical center-point of the molecule does not change its position; hence the name point group. One can determine the elements of the point group for a particular molecule by considering the geometrical symmetry of its molecular model. However, when one uses a point group, the elements are not to be interpreted in the same way. Instead the elements rotate and/or reflect the vibronic (vibration-electronic) coordinates and these elements commute with the vibronic Hamiltonian. The point group is used to classify by symmetry the vibronic eigenstates. The symmetry classification of the rotational levels, the eigenstates of the full (rovibronic nuclear spin) Hamiltonian, requires the use of the appropriate permutation-inversion group as introduced by Longuet-Higgins. See the Section Inversion symmetry and nuclear permutation symmetry below. The elements of permutation-inversion groups commute with the full molecular Hamiltonian. In addition to point groups, there exists another kind of group important in crystallography, where translation in 3-D also needs to be taken care of. They are known as space groups.

Basic point group symmetry operations

The five basic symmetry operations mentioned above are:

1. Identity Operation E (from the German 'Einheit' meaning unity): The identity operation leaves the molecule unchanged. It forms the identity element in the symmetry group. Though its inclusion seems to be trivial, it is important also because even for the most asymmetric molecule, this symmetry is present. The corresponding symmetry element is the entire molecule itself.
2. Inversion, i : This operation inverts the molecule about its center of inversion (if it has any). The center of inversion is the symmetry element in this case. There may or may not be an atom at this center. A molecule may or may not have a center of inversion. For example: the benzene molecule, a cube, and spheres do have a center of inversion, whereas a tetrahedron does not.
3. Reflection σ: The reflection operation produces a mirror image geometry of the molecule about a certain plane. The mirror plane bisects the molecule and must include its center of geometry. The plane of symmetry is the symmetry element in this case. A symmetry plane parallel with the principal axis (defined below) is dubbed vertical (σ_v) and one perpendicular to it horizontal (σ_h). A third type of symmetry plane exists: If a vertical symmetry plane additionally bisects the angle between two 2-fold rotation axes perpendicular to the principal axis, the plane is dubbed dihedral (σ_d).
4. n-Fold Rotation [math]\displaystyle{ {{c}_{n}} }[/math]: The n-fold rotation operation about a n-fold axis of symmetry  produces molecular orientations indistinguishable from the initial for each rotation of  [math]\displaystyle{ \frac{{{360}^{0}}}{n} }[/math] (clockwise and counter-clockwise).It is denoted by [math]\displaystyle{ {{c}_{n}} }[/math]. The axis of symmetry is the symmetry element in this case. A molecule can have more than one symmetry axis; the one with the highest n is called the principal axis, and by convention is assigned the z-axis in a Cartesian coordinate system.
5. n-Fold Rotation-Reflection or improper rotation S_n : The n-fold improper rotation operation about an n-fold axis of improper rotation is composed of two successive geometry transformations: first, a rotation through [math]\displaystyle{ \frac{{{360}^{0}}}{n} }[/math] about the axis of that rotation, and second, reflection through a plane perpendicular (and through the molecular center of geometry) to that axis. This axis is the symmetry element in this case. It is abbreviated S_n.

All other symmetry present in a specific molecule are a combination of these 5 operations.

Schoenflies notation

The Schoenflies (or Schönflies) notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe point groups. This notation is used in spectroscopy and is used here to specify a molecular point group.

Point groups for diatomic molecules

There are two point groups for diatomic molecules: [math]\displaystyle{ }[/math] for heteronuclear diatomics, and [math]\displaystyle{ }[/math] for homonuclear diatomics.

• [math]\displaystyle{ }[/math]:

The group [math]\displaystyle{ }[/math], contains rotations [math]\displaystyle{ C(\phi) }[/math] through any angle [math]\displaystyle{ \phi }[/math] about the axis of symmetry and an infinite number of reflections [math]\displaystyle{ {{\sigma }_{v}} }[/math] through the planes containing the inter-nuclear axis (or the vertical axis, that is reason of the subscript 'v').In the group [math]\displaystyle{ }[/math] all planes of symmetry are equivalent, so that all reflections [math]\displaystyle{ {{\sigma }_{v}} }[/math] form a single class with a continuous series of elements; the axis of symmetry is bilateral, so that there is a continuous series of classes, each containing two elements [math]\displaystyle{ C(\pm \phi) }[/math]. Note that this group is non-abelian and there exists an infinite number of irreducible representations in the group. The character table of the group is as follows:

	E	2c∞[math]\displaystyle{ {\phi} }[/math]	...	[math]\displaystyle{ \infty {{\sigma }_{v}} }[/math]	linear functions, rotations	quadratic
A1=Σ+	1	1	...	1	z	x2+y2, z2
A2=Σ−	1	1	...	-1	Rz
E1=Π	2	[math]\displaystyle{ 2\cos (\phi) }[/math]	...	0	(x, y) (Rx, Ry)	(xz, yz)
E2=Δ	2	[math]\displaystyle{ 2\cos (2\phi) }[/math]	...	0		(x2-y2, xy)
E3=Φ	2	[math]\displaystyle{ 2\cos (3\phi) }[/math]	....	0
...	...	...	...

• [math]\displaystyle{ {{D}_{\infty h}} }[/math]:

In addition to axial reflection symmetry, homonuclear diatomic molecules are symmetric with respect to inversion or reflection through any axis in the plane passing through the point of symmetry and perpendicular to the inter-nuclear axis.

Inversion symmetry in homonuclear diatomic molecules, giving rise to symmetry group [math]\displaystyle{ {{D}_{\infty h}} }[/math]

The classes of the group [math]\displaystyle{ {{D}_{\infty h}} }[/math] can be obtained from those of the group [math]\displaystyle{ }[/math] using the relation between the two groups: [math]\displaystyle{ {{D}_{\infty h}}={{C}_{\infty v}}\times {{C}_{i}} }[/math]. Like [math]\displaystyle{ }[/math], [math]\displaystyle{ {{D}_{\infty h}} }[/math] is non-abelian and there are an infinite number of irreducible representations in the group. The character table of this group is as follows:

	E	2c∞[math]\displaystyle{ {\phi} }[/math]	...	[math]\displaystyle{ \infty {{\sigma }_{h}} }[/math]	i	2S∞[math]\displaystyle{ {\phi} }[/math]	...	[math]\displaystyle{ \infty }[/math][math]\displaystyle{ c_{2}^{'} }[/math]	linear functions, rotations	quadratic
A1g=Σ+g	1	1	...	1	1	1	...		z	x2+y2, z2
A2g=Σ−g	1	1	...	-1	1	1	...		Rz
E1g=Πg	2	[math]\displaystyle{ 2\cos (\phi) }[/math]	...	0	2	[math]\displaystyle{ -2\cos (\phi) }[/math]	...		(x, y) (Rx, Ry)	(xz, yz)
E2g=Δg	2	[math]\displaystyle{ 2\cos (2\phi) }[/math]	...	0	2	[math]\displaystyle{ 2\cos (2\phi) }[/math]	...			(x2-y2, xy)
E3g=Φg	2	[math]\displaystyle{ 2\cos (3\phi) }[/math]	....	0	2	[math]\displaystyle{ -2\cos (3\phi) }[/math]	...
...	...	...	...	...	...	...	...
A1u=Σ+u	1	1	...	1	-1	-1	...		z
A2u=Σ−u	1	1	...	-1	-1	-1	...
E1u=Πu	2	[math]\displaystyle{ 2\cos (\phi) }[/math]	...	0	-2	[math]\displaystyle{ 2\cos (\phi) }[/math]	...		(x, y)
E2u=Δu	2	[math]\displaystyle{ 2\cos (2\phi) }[/math]	...	0	-2	[math]\displaystyle{ -2\cos (2\phi) }[/math]	...
E3u=Φu	2	[math]\displaystyle{ 2\cos (3\phi) }[/math]	...	0	-2	[math]\displaystyle{ 2\cos (3\phi) }[/math]	...
...	...	...	...	...	...	...	...

Summary examples

Point group	Symmetry operations or group operations	Symmetry elements or group elements	Simple description of typical geometry	Group order	Number of classes and irreducible representations (irreps)	Example
[math]\displaystyle{ }[/math]	E, [math]\displaystyle{ c_{_{\infty }}^{\phi } }[/math] ,σv	E, [math]\displaystyle{ 2c_{_{\infty }} }[/math] ,[math]\displaystyle{ \infty {{\sigma }_{v}} }[/math]	linear	[math]\displaystyle{ \infty }[/math]	[math]\displaystyle{ \infty }[/math]	Hydrogen fluoride
[math]\displaystyle{ {{D}_{\infty h}} }[/math]	E, [math]\displaystyle{ c_{_{\infty }}^{\phi } }[/math], σh ,i,[math]\displaystyle{ c_{2}^{'} }[/math]	S∞ ,E ,[math]\displaystyle{ 2c_{_{\infty }} }[/math] ,[math]\displaystyle{ \infty {{\sigma }_{h}} }[/math],[math]\displaystyle{ \infty }[/math][math]\displaystyle{ c_{2}^{'} }[/math]	linear with inversion center	[math]\displaystyle{ \infty }[/math]	[math]\displaystyle{ \infty }[/math]	oxygen

Complete set of commuting operators

Unlike a single atom, the Hamiltonian of a diatomic molecule doesn't commute with [math]\displaystyle{ {{L}^{2}} }[/math]. So the quantum number [math]\displaystyle{ l }[/math] is no longer a good quantum number. The internuclear axis chooses a specific direction in space and the potential is no longer spherically symmetric. Instead, [math]\displaystyle{ {{L}_{z}} }[/math] and [math]\displaystyle{ {{J}_{z}} }[/math] commutes with the Hamiltonian [math]\displaystyle{ H }[/math] (taking the arbitrary internuclear axis as the Z axis). But [math]\displaystyle{ {{L}_{x}},{{L}_{y}} }[/math] do not commute with [math]\displaystyle{ H }[/math] due to the fact that the electronic Hamiltonian of a diatomic molecule is invariant under rotations about the internuclear line (the Z axis), but not under rotations about the X or Y axes. Again, [math]\displaystyle{ {{S}^{2}} }[/math] and [math]\displaystyle{ {{S}_{z}} }[/math] act on a different Hilbert space, so they commute with [math]\displaystyle{ H }[/math] in this case also. The electronic Hamiltonian for a diatomic molecule is also invariant under reflections in all planes containing the internuclear line. The (X-Z) plane is such a plane, and reflection of the coordinates of the electrons in this plane corresponds to the operation [math]\displaystyle{ {{y}_{i}}\to -{{y}_{i}} }[/math]. If [math]\displaystyle{ {{A}_{y}} }[/math] is the operator that performs this reflection, then [math]\displaystyle{ [{{A}_{y}},H]=0 }[/math]. So the Complete Set of Commuting Operators (CSCO) for a general heteronuclear diatomic molecule is [math]\displaystyle{ \{H,\text{ }{{J}_{z}},{{L}_{z}},{{S}^{2}},{{S}_{z}},A\} }[/math]; where [math]\displaystyle{ A }[/math] is an operator that inverts only one of the two spatial co-ordinates (x or y).

In the special case of a homonuclear diatomic molecule, there is an extra symmetry since in addition to the axis of symmetry provided by the internuclear axis, there is a centre of symmetry at the midpoint of the distance between the two nuclei (the symmetry discussed in this paragraph only depends on the two nuclear charges being the same. The two nuclei can therefore have different mass, that is they can be two isotopes of the same species such as the proton and the deuteron, or [math]\displaystyle{ {{O}^{16}} }[/math] and [math]\displaystyle{ {{O}^{18}} }[/math], and so on). Choosing this point as the origin of the coordinates, the Hamiltonian is invariant under an inversion of the coordinates of all electrons with respect to that origin, namely in the operation [math]\displaystyle{ {{\vec{r}}_{i}}\to -{{\vec{r}}_{i}} }[/math]. Thus the parity operator [math]\displaystyle{ \Pi }[/math]. Thus the CSCO for a homonuclear diatomic molecule is [math]\displaystyle{ \left\{ H,\text{ }{{J}_{z}},{{L}_{z}},{{S}^{2}},{{S}_{z}},A,\text{ }\Pi \right\} }[/math].

Molecular term symbol, Λ-doubling

Molecular term symbol is a shorthand expression of the group representation and angular momenta that characterize the state of a molecule. It is the equivalent of the term symbol for the atomic case. We already know the CSCO of the most general diatomic molecule. So, the good quantum numbers can sufficiently describe the state of the diatomic molecule. Here, the symmetry is explicitly stated in the nomenclature.

Angular momentum

Here, the system is not spherically symmetric. So, [math]\displaystyle{ [H,{{L}^{2}}]\ne 0 }[/math], and the state cannot be depicted in terms of [math]\displaystyle{ l }[/math] as an eigenstate of the Hamiltonian is not an eigenstate of [math]\displaystyle{ {{L}^{2}} }[/math] anymore (in contrast to the atomic term symbol, where the states were written as [math]\displaystyle{ ^{2S+1}{{L}_{J}} }[/math]). But, as [math]\displaystyle{ [H,{{L}_{z}}]= 0 }[/math], the eigenvalues corresponding to [math]\displaystyle{ {{L}_{z}} }[/math] can still be used. If,

[math]\displaystyle{ \begin{align} & {{L}_{z}}\left| \Psi \right\rangle ={{M}_{L}}\hbar \left| \Psi \right\rangle ;{{M}_{L}}=0,\pm 1,\pm 2,.......... \\ & \Rightarrow {{L}_{z}}\left| \Psi \right\rangle =\pm \Lambda \hbar \left| \Psi \right\rangle ;\Lambda =0,1,2,........... \\ \end{align} }[/math]

where [math]\displaystyle{ \Lambda =\left| {{M}_{L}} \right| }[/math] is the absolute value (in a.u.) of the projection of the total electronic angular momentum on the internuclear axis; [math]\displaystyle{ \Lambda }[/math] can be used as a term symbol. By analogy with the spectroscopic notation S, P, D, F, ... used for atoms, it is customary to associate code letters with the values of [math]\displaystyle{ \Lambda }[/math] according to the correspondence:

For the individual electrons, the notation and the correspondence used are:

[math]\displaystyle{ \lambda =\left| {{m}_{l}} \right| }[/math] and

Axial symmetry

Again, [math]\displaystyle{ [{{A}_{y}},H]=0 }[/math], and in addition: [math]\displaystyle{ {{A}_{y}}{{L}_{z}}=-{{L}_{z}}{{A}_{y}} }[/math] [as [math]\displaystyle{ {{L}_{z}}=-i\hbar (x\frac{\partial }{\partial y}-y\frac{\partial }{\partial x}) }[/math]]. It follows immediately that if [math]\displaystyle{ \Lambda \ne 0 }[/math] the action of the operator [math]\displaystyle{ {{A}_{y}} }[/math] on an eigenstate corresponding to the eigenvalue [math]\displaystyle{ \Lambda \hbar }[/math] of [math]\displaystyle{ {{L}}_{{z}} }[/math] converts this state into another one corresponding to the eigenvalue [math]\displaystyle{ -\Lambda \hbar }[/math], and that both eigenstates have the same energy. The electronic terms such that [math]\displaystyle{ \Lambda \ne 0 }[/math] (that is, the terms [math]\displaystyle{ \Pi ,\Delta ,\Phi ,................ }[/math]) are thus doubly degenerate, each value of the energy corresponding to two states which differ by the direction of the projection of the orbital angular momentum along the molecular axis. This twofold degeneracy is actually only approximate and it is possible to show that the interaction between the electronic and rotational motions leads to a splitting of the terms with [math]\displaystyle{ \Lambda \ne 0 }[/math] into two nearby levels, which is called [math]\displaystyle{ \Lambda }[/math]-doubling.

[math]\displaystyle{ \Lambda=0 }[/math] corresponds to the [math]\displaystyle{ \Sigma }[/math] states. These states are non-degenerate, so that the states of a [math]\displaystyle{ \Sigma }[/math] term can only be multiplied by a constant in a reflection through a plane containing the molecular axis. When [math]\displaystyle{ \Lambda=0 }[/math], simultaneous eigenfunctions of [math]\displaystyle{ H }[/math],[math]\displaystyle{ {{L}}_{{z}} }[/math] and [math]\displaystyle{ {{A}}_{{y}} }[/math] can be constructed. Since [math]\displaystyle{ A_{y}^{2}=1 }[/math], the eigenfunctions of [math]\displaystyle{ {{A}}_{{y}} }[/math] have eigenvalues [math]\displaystyle{ \pm 1 }[/math]. So to completely specify [math]\displaystyle{ \Sigma }[/math] states of diatomic molecules, [math]\displaystyle{ {{\Sigma }^{+}} }[/math] states, which is left unchanged upon reflection in a plane containing the nuclei, needs to be distinguished from [math]\displaystyle{ {{\Sigma }^{-}} }[/math] states, for which it changes sign in performing that operation.

Inversion symmetry and nuclear permutation symmetry

Homonuclear diatomic molecules have a center of symmetry at their midpoint. Choosing this point (which is the nuclear center of mass) as the origin of the coordinates, the electronic Hamiltonian is invariant under the point group operation i of inversion of the coordinates of all electrons at that origin. This operation is not the parity operation P (or E*); the parity operation involves the inversion of nuclear and electronic spatial coordinates at the molecular center of mass. Electronic states either remain unchanged by the operation i, or they are changed in sign by i. The former are denoted by the subscript g and are called gerade, while the latter are denoted by the subscript u and are called ungerade. The subscripts g or u are therefore added to the term symbol, so that for homonuclear diatomic molecules electronic states can have the symmetries [math]\displaystyle{ \Sigma _{g}^{+},\Sigma _{g}^{-},\Sigma _{u}^{+},\Sigma _{u}^{-},{{\Pi }_{g}},{{\Pi }_{u}} }[/math],......according to the irreducible representations of the [math]\displaystyle{ {{D}_{\infty h}} }[/math] point group.

The complete Hamiltonian of a diatomic molecule (as for all molecules) commutes with the parity operation P or E* and rovibronic (rotation-vibration-electronic) energy levels (often called rotational levels) can be given the parity symmetry label + or -. The complete Hamiltonian of a homonuclear diatomic molecule also commutes with the operation of permuting (or exchanging) the coordinates of the two (identical) nuclei and rotational levels gain the additional label s or a depending on whether the total wavefunction is unchanged (symmetric) or changed in sign (antisymmetric) by the permutation operation. Thus, the rotational levels of heteronuclear diatomic molecules are labelled + or -, whereas those of homonuclear diatomic molecules are labelled +s, +a, -s or -a. The rovibronic nuclear spin states are classified using the appropriate permutation-inversion group.

The complete Hamiltonian of a homonuclear diatomic molecule (as for all centro-symmetric molecules) does not commute with the point group inversion operation i because of the effect of the nuclear hyperfine Hamiltonian. The nuclear hyperfine Hamiltonian can mix the rotational levels of g and u vibronic states (called ortho-para mixing) and give rise to ortho-para transitions

Spin and total angular momentum

If S denotes the resultant of the individual electron spins, [math]\displaystyle{ s(s+1){{\hbar }^{2}} }[/math] are the eigenvalues of S and as in the case of atoms, each electronic term of the molecule is also characterised by the value of S. If spin-orbit coupling is neglected, there is a degeneracy of order [math]\displaystyle{ 2s+1 }[/math] associated with each [math]\displaystyle{ s }[/math] for a given [math]\displaystyle{ \Lambda }[/math]. Just as for atoms, the quantity [math]\displaystyle{ 2s+1 }[/math] is called the multiplicity of the term and.is written as a (left) superscript, so that the term symbol is written as [math]\displaystyle{ {}^{2s+1}\Lambda }[/math]. For example, the symbol [math]\displaystyle{ {}^{3}\Pi }[/math]denotes a term such that [math]\displaystyle{ \Lambda = 1 }[/math] and [math]\displaystyle{ s=1 }[/math]. It is worth noting that the ground state (often labelled by the symbol [math]\displaystyle{ X }[/math]) of most diatomic molecules is such that [math]\displaystyle{ s=0 }[/math] and exhibits maximum symmetry. Thus, in most cases it is a [math]\displaystyle{ {}^{1}{{\Sigma }^{+}} }[/math] state (written as [math]\displaystyle{ X{}^{1}{{\Sigma }^{+}} }[/math], excited states are written with [math]\displaystyle{ A,B,C,... }[/math] in front) for a heteronuclear molecule and a [math]\displaystyle{ {}^{1}\Sigma _{g}^{+} }[/math] state (written as [math]\displaystyle{ X{}^{1}\Sigma _{g}^{+} }[/math]) for a homonuclear molecule.

Spin–orbit coupling lifts the degeneracy of the electronic states. This is because the z-component of spin interacts with the z-component of the orbital angular momentum, generating a total electronic angular momentum along the molecule axis J_z. This is characterized by the quantum number [math]\displaystyle{ {{M}_{J}} }[/math], where [math]\displaystyle{ {{M}_{J}}={{M}_{S}}+{{M}_{L}} }[/math]. Again, positive and negative values of [math]\displaystyle{ {{M}_{J}} }[/math] are degenerate, so the pairs (M_L, M_S) and (−M_L, −M_S) are degenerate. These pairs are grouped together with the quantum number [math]\displaystyle{ \Omega }[/math], which is defined as the sum of the pair of values (M_L, M_S) for which M_L is positive: [math]\displaystyle{ \Omega =\Lambda +{{M}_{S}} }[/math]

Molecular term symbol

So, the overall molecular term symbol for the most general diatomic molecule is given by:

[math]\displaystyle{ {}^{2S+1}\!\Lambda^{(+/-)}_{\Omega,(g/u)} }[/math]

where

• S is the total spin quantum number
• [math]\displaystyle{ \Lambda }[/math] is the projection of the orbital angular momentum along the internuclear axis
• [math]\displaystyle{ \Omega }[/math] is the projection of the total angular momentum along the internuclear axis
• u/g is the effect of the point group operation i
• +/− is the reflection symmetry along an arbitrary plane containing the internuclear axis

von Neumann-Wigner non-crossing rule

Effect of symmetry on the matrix elements of the Hamiltonian

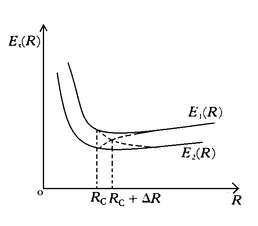
The electronic terms or potential curves [math]\displaystyle{ {{E}_{S}}(R) }[/math] of a diatomic molecule depend only on the internuclear distance [math]\displaystyle{ R }[/math], and it is important to investigate the behaviour of these potential curves as R varies. It is of considerable interest to examine the intersection of the curves representing the different terms.

The non-crossing rule of von Neumann and Wigner. Two potential curves [math]\displaystyle{ {{E}_{1}}(R) }[/math] and [math]\displaystyle{ {{E}_{2}}(R) }[/math] cannot cross if the states 1 and 2 have the same point group symmetry

Let [math]\displaystyle{ {{E}_{1}}(R) }[/math] and [math]\displaystyle{ {{E}_{2}}(R) }[/math] two different electronic potential curves. If they intersect at some point, then the functions [math]\displaystyle{ {{E}_{1}}(R) }[/math] and [math]\displaystyle{ {{E}_{2}}(R) }[/math] will have neighbouring values near this point. To decide whether such an intersection can occur, it is convenient to put the problem as follows. Suppose at some internuclear distance [math]\displaystyle{ {{R}}_{{c}} }[/math] the values [math]\displaystyle{ {{E}_{1}}({{R}_{C}}) }[/math] and [math]\displaystyle{ {{E}_{2}}({{R}_{C}}) }[/math] are close, but distinct (as shown in the figure). Then it is to be examined whether or [math]\displaystyle{ {{E}_{1}}(R) }[/math] and [math]\displaystyle{ {{E}_{2}}(R) }[/math] can be made to intersect by the modification [math]\displaystyle{ {{R}_{C}}\to {{R}_{C}}+\Delta R }[/math]. The energies [math]\displaystyle{ E_{1}^{(0)}={{E}_{1}}({{R}_{C}}) }[/math] and [math]\displaystyle{ E_{2}^{(0)}={{E}_{2}}({{R}_{C}}) }[/math] are eigenvalues of the Hamiltonian [math]\displaystyle{ {{H}_{0}}=H({{R}_{C}}) }[/math]. The corresponding orthonormal electronic eigenstates will be denoted by [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] and are assumed to be real. The Hamiltonian now becomes [math]\displaystyle{ H\equiv H({{R}_{C}}+\Delta R)={{H}_{0}}+H' }[/math], where [math]\displaystyle{ H'=\frac{\partial {{H}_{0}}}{\partial {{R}_{C}}}\Delta R }[/math] is the small perturbation operator (though it is a degenerate case, so ordinary method of perturbation won't work). setting [math]\displaystyle{ H_{ij}^{'}=\left\langle \Phi _{i}^{(0)}|H'|\Phi _{j}^{(0)} \right\rangle ;i,j=1,2 }[/math], it can be deduced that in order for [math]\displaystyle{ {{E}_{1}}(R) }[/math] and [math]\displaystyle{ {{E}_{2}}(R) }[/math] to be equal at the point [math]\displaystyle{ {{R}_{C}}+\Delta R }[/math] the following two conditions are required to be fulfilled:

[math]\displaystyle{ E_{1}^{(0)}-E_{2}^{(0)}+H_{11}^{'}-H_{22}^{'}=0 }[/math] and [math]\displaystyle{ H_{12}^{'}=0 }[/math]

As an initial zero-order approximation, instead of [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] themselves, linear combinations of them of the form [math]\displaystyle{ \left| {{\Phi }^{(0)}} \right\rangle ={{c}_{1}}\left| \Phi _{1}^{(0)} \right\rangle +{{c}_{2}}\left| \Phi _{2}^{(0)} \right\rangle }[/math], can be taken as the eigenstate of the Hamiltonian [math]\displaystyle{ H }[/math] (where [math]\displaystyle{ {{c}_{1}} }[/math] and [math]\displaystyle{ {{c}_{2}} }[/math] are, in general, complex). Substituting this expression in the perturbed Schrödinger  equation: [math]\displaystyle{ ({{H}_{0}}+H')\left| {{\Phi }^{(0)}} \right\rangle =E\left| {{\Phi }^{(0)}} \right\rangle }[/math] Expanding: [math]\displaystyle{ {{c}_{1}}(E_{1}^{(0)}+H'-E)\left| \Phi _{1}^{(0)} \right\rangle +{{c}_{2}}(E_{2}^{(0)}+H'-E)\left| \Phi _{2}^{(0)} \right\rangle =0 }[/math] Taking inner product with the respective bra's: [math]\displaystyle{ {{c}_{1}}(E_{1}^{(0)}+H'-E)\left\langle \Phi _{1}^{(0)}|\Phi _{1}^{(0)} \right\rangle +{{c}_{2}}(E_{2}^{(0)}+H'-E)\left\langle \Phi _{1}^{(0)}|\Phi _{2}^{(0)} \right\rangle =0 }[/math]; and [math]\displaystyle{ {{c}_{1}}(E_{1}^{(0)}+H'-E)\left\langle \Phi _{2}^{(0)}|\Phi _{1}^{(0)} \right\rangle +{{c}_{2}}(E_{2}^{(0)}+H'-E)\left\langle \Phi _{2}^{(0)}|\Phi _{2}^{(0)} \right\rangle =0 }[/math] Now, [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] are eigenstates of the Hamiltonian [math]\displaystyle{ }[/math] corresponding to different eigenvalues and as [math]\displaystyle{ }[/math] is itself Hermitian, they are orthonormal: [math]\displaystyle{ \left\langle \Phi _{i}^{(0)}|\Phi _{j}^{(0)} \right\rangle ={{\delta }_{ij}} }[/math] Thus: [math]\displaystyle{ {{c}_{1}}(E_{1}^{(0)}+H_{11}^{'}-E)+{{c}_{2}}H_{12}^{'}=0 }[/math]; and [math]\displaystyle{ {{c}_{1}}H_{21}^{'}+{{c}_{2}}(E_{2}^{(0)}+H_{22}^{'}-E)=0 }[/math] Since the operator [math]\displaystyle{ H' }[/math] is Hermitian, the matrix elements [math]\displaystyle{ H_{11}^{'} }[/math] and [math]\displaystyle{ H_{22}^{'} }[/math] are real, while [math]\displaystyle{ H_{12}^{'}=H_{21}^{'*} }[/math]. The compatibility condition for these equations is (such that both [math]\displaystyle{ {{c}_{1}} }[/math] and [math]\displaystyle{ {{c}_{2}} }[/math] are not simultaneously zero): [math]\displaystyle{ \left| \begin{matrix} E_{1}^{(0)}+H_{11}^{'}-E & H_{12}^{'} \\ H_{21}^{'} & E_{2}^{(0)}+H_{22}^{'}-E \\ \end{matrix} \right|=0 }[/math] This gives: [math]\displaystyle{ E=\frac{1}{2}(E_{1}^{(0)}+E_{2}^{(0)}+H_{11}^{'}+H_{22}^{'})\pm \sqrt{\frac{1}{4}{{(E_{1}^{(0)}-E_{2}^{(0)}+H_{11}^{'}-H_{22}^{'})}^{2}}+{{\left| H_{12}^{'} \right|}^{2}}} }[/math] This formula gives the required eigenvalues of the energy in the first approximation. If the energy values of the two terms become equal at the point [math]\displaystyle{ ({{R}_{C}}+\Delta R) }[/math] (i.e. the terms intersect), this means that the two values of [math]\displaystyle{ E }[/math] given by formula, are the same. For this to happen, the expression under the radical must vanish. Since it is the sum of two squares, both are simultaneously zero. So, it gives the conditions: [math]\displaystyle{ E_{1}^{(0)}-E_{2}^{(0)}+H_{11}^{'}-H_{22}^{'}=0 }[/math] and [math]\displaystyle{ H_{12}^{'}=0 }[/math]

However, we have at our disposal only one arbitrary parameter [math]\displaystyle{ \Delta R }[/math] giving the perturbation [math]\displaystyle{ H' }[/math]. Hence the

two conditions involving more than one parameter cannot in general be simultaneously satisfied (the initial assumption that [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] real, implies that [math]\displaystyle{ H_{12}^{'} }[/math] is also real). So, two case can arise: 

1. The matrix element [math]\displaystyle{ H_{12}^{'} }[/math] vanishes identically. It is then possible to satisfy the first condition independently. Therefore, it is possible for the crossing to occur if, for a certain value of [math]\displaystyle{ \Delta R }[/math] (i.e., for a certain value of [math]\displaystyle{ R }[/math]) the first equation is satisfied. As the perturbation operator [math]\displaystyle{ H' }[/math] (or [math]\displaystyle{ H }[/math]) commutes with the symmetry operators of the molecule, this case will happen if the two electronic states [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] have different point group symmetries (for example if they correspond to two electronic terms having different values of [math]\displaystyle{ \Lambda }[/math], different electronic parities g and u, different multiplicities, or for example are the two terms [math]\displaystyle{ {{\Sigma }^{+}} }[/math]) as it can be shown that, for a scalar quantity whose operator commutes with the angular momentum and inversion operators, only the matrix elements for transitions between states of the same angular momentum and parity are non-zero and the proof remains valid, in essentially the same form, for the general case of an arbitrary symmetry operator.  
2. If the electronic states [math]\displaystyle{ \left| \Phi _{1}^{(0)} \right\rangle }[/math] and [math]\displaystyle{ \left| \Phi _{2}^{(0)} \right\rangle }[/math] have the same point group symmetry, then [math]\displaystyle{ H_{12}^{'} }[/math] can be, and will in general be, non-zero. Except for accidental crossing which would occur if, by coincidence, the two equations were satisfied at the same value of [math]\displaystyle{ R }[/math], it is in general impossible to find a single value of [math]\displaystyle{ \Delta R }[/math] (i.e., a single value of [math]\displaystyle{ R }[/math]) for which the two conditions are satisfied simultaneously.  

Thus, in a diatomic molecule, only terms of different symmetry can intersect, while the intersection of terms of like symmetry is forbidden. This is, in general, true for any case in quantum mechanics where the Hamiltonian contains some parameter and its eigenvalues are consequently functions of that parameter. This general rule is known as von Neumann - Wigner non-crossing rule.

This general symmetry principle has important consequences is molecular spectra. In fact, in the applications of valence bond method in case of diatomic molecules, three main correspondence between the atomic and the molecular orbitals are taken care of:

1. Molecular orbitals having a given value of [math]\displaystyle{ \lambda }[/math] (the component of the orbital angular momentum along the internuclear axis) must connect with atomic orbitals having the same value of [math]\displaystyle{ \lambda }[/math] (i.e. the same value of [math]\displaystyle{ \left| m \right| }[/math]).
2. The electronic parity of the wave function (g or u) must be preserved as [math]\displaystyle{ R }[/math] varies from [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ \infty }[/math].
3. The von Neumann-Wigner non-crossing rule must be obeyed, so that energy curves corresponding to orbitals having the same symmetry do not cross as [math]\displaystyle{ R }[/math] varies from [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ \infty }[/math].

Thus, von Neumann-Wigner non-crossing rule also acts as a starting point for valence bond theory.

Observable consequences

Symmetry in diatomic molecules manifests itself directly by influencing the molecular spectra of the molecule. The effect of symmetry on different types of spectra in diatomic molecules are:

Rotational spectrum

In the electric dipole approximation the transition amplitude for emission or absorption of radiation can be shown to be proportional to the vibronic matrix element of the component of the electric dipole operator [math]\displaystyle{ D }[/math] along the molecular axis. This is the permanent electric dipole moment. In homonuclear diatomic molecules, the permanent electric dipole moment vanishes and there is no pure rotation spectrum (but see N.B. below). Heteronuclear diatomic molecules possess a permanent electric dipole moment and exhibit spectra corresponding to rotational transitions, without change in the vibronic state. For [math]\displaystyle{ \Lambda =0 }[/math], the selection rules for a rotational transition are: [math]\displaystyle{ \begin{align} & \Delta \Im =\pm 1 \\ & \Delta {{M}_{\Im }}=0,\pm 1 \\ \end{align} }[/math]. For [math]\displaystyle{ \Lambda \ne 0 }[/math], the selection rules become: [math]\displaystyle{ \begin{align} & \Delta \Im =0,\pm 1 \\ & \Delta {{M}_{\Im }}=0,\pm 1 \\ \end{align} }[/math].This is due to the fact that although the photon absorbed or emitted carries one unit of angular momentum, the nuclear rotation can change, with no change in [math]\displaystyle{ \Im }[/math], if the electronic angular momentum makes an equal and opposite change. Symmetry considerations require that the electric dipole moment of a diatomic molecule is directed along the internuclear line, and this leads to the additional selection rule [math]\displaystyle{ \Delta \Lambda =0 }[/math].The pure rotational spectrum of a diatomic molecule consists of lines in the far infra-red or the microwave region, the frequencies of these lines given by:

[math]\displaystyle{ \hbar {{\omega }_{\Im +1,\Im }}={{E}_{r}}(\Im +1)-{{E}_{r}}(\Im)=2B(\Im +1) }[/math]; where [math]\displaystyle{ B=\frac{{{\hbar }^{2}}}{2\mu R_{0}^{2}} }[/math], and [math]\displaystyle{ \Im \ge \Lambda }[/math]

• N.B. In exceptional circumstances the hyperfine Hamiltonian can mix the rotational levels of g and u vibronic states of homonuclear diatomic molecules giving rise to pure rotational (ortho - para) transitions in a homonuclear diatomic molecule.

Vibrational spectrum

The transition matrix elements for pure vibrational transition are [math]\displaystyle{ {{\mu }_{v,v'}}=\left\langle v'|\mu |v \right\rangle }[/math], where [math]\displaystyle{ \mu }[/math] is the dipole moment of the diatomic molecule in the electronic state [math]\displaystyle{ \alpha }[/math]. Because the dipole moment depends on the bond length [math]\displaystyle{ R }[/math], its variation with displacement of the nuclei from equilibrium can be expressed as: [math]\displaystyle{ \mu ={{\mu }_{0}}+{{(\frac{d\mu }{dx})}_{0}}x+\frac{1}{2}{{(\frac{{{d}^{2}}\mu }{d{{x}^{2}}})}_{0}}{{x}^{2}}+....... }[/math]; where [math]\displaystyle{ {{\mu }_{0}} }[/math] is the dipole moment when the displacement is zero. The transition matrix elements are, therefore: [math]\displaystyle{ \left\langle v'|\mu |v \right\rangle ={{\mu }_{0}}\left\langle v'|v \right\rangle +{{(\frac{d\mu }{dx})}_{0}}\left\langle v'|x|v \right\rangle +\frac{1}{2}{{(\frac{{{d}^{2}}\mu }{d{{x}^{2}}})}_{0}}\left\langle v'|{{x}^{2}}|v \right\rangle +.......={{(\frac{d\mu }{dx})}_{0}}\left\langle v'|x|v \right\rangle +\frac{1}{2}{{(\frac{{{d}^{2}}\mu }{d{{x}^{2}}})}_{0}}\left\langle v'|{{x}^{2}}|v \right\rangle +....... }[/math]using orthogonality of the states. So, the transition matrix is non-zero only if the molecular dipole moment varies with displacement, for otherwise the derivatives of [math]\displaystyle{ \mu }[/math] would be zero. The gross selection rule for the vibrational transitions of diatomic molecules is then: To show a vibrational spectrum, a diatomic molecule must have a dipole moment that varies with extension. So, homonuclear diatomic molecules do not undergo electric-dipole vibrational transitions. So, a homonuclear diatomic molecule doesn't show purely vibrational spectra.

For small displacements, the electric dipole moment of a molecule can be expected to vary linearly with the extension of the bond. This would be the case for a heteronuclear molecule in which the partial charges on the two atoms were independent of the internuclear distance. In such cases (known as harmonic approximation), the quadratic and higher terms in the expansion can be ignored and [math]\displaystyle{ {{\mu }_{v,v'}}=\left\langle v'|\mu |v \right\rangle ={{(\frac{d\mu }{dx})}_{0}}\left\langle v'|x|v \right\rangle }[/math]. Now, the matrix elements can be expressed in position basis in terms of the harmonic oscillator wavefunctions: Hermite polynomials. Using the property of Hermite polynomials: [math]\displaystyle{ 2(\alpha x){{H}_{v}}(\alpha x)=2v{{H}_{v-1}}(\alpha x)+{{H}_{v+1}}(\alpha x) }[/math], it is evident that [math]\displaystyle{ x\left| v \right\rangle }[/math] which is proportional to [math]\displaystyle{ x{{H}_{v}}(\alpha x) }[/math], produces two terms, one proportional to [math]\displaystyle{ \left| v+1 \right\rangle }[/math] and the other to [math]\displaystyle{ \left| v-1 \right\rangle }[/math]. So, the only non-zero contributions to [math]\displaystyle{ {{\mu }_{v,v'}} }[/math] comes from [math]\displaystyle{ v'=v\pm 1 }[/math]. So, the selection rule for heteronuclear diatomic molecules is: [math]\displaystyle{ \Delta v=\pm 1 }[/math]

• Conclusion: Homonuclear diatomic molecules show no pure vibrational spectral lines, and the vibrational spectral lines of heteronuclear diatomic molecules are governed by the above-mentioned selection rule.

Rovibrational spectrum

Homonuclear diatomic molecules show neither pure vibrational nor pure rotational spectra. However, as the absorption of a photon requires the molecule to take up one unit of angular momentum, vibrational transitions are accompanied by a change in rotational state, which is subject to the same selection rules as for the pure rotational spectrum. For a molecule in a [math]\displaystyle{ \Sigma }[/math] state, the transitions between two vibration-rotation (or rovibrational) levels [math]\displaystyle{ (v,\Im) }[/math] and [math]\displaystyle{ (v',\Im') }[/math], with vibrational quantum numbers [math]\displaystyle{ v }[/math] and [math]\displaystyle{ v' = v + 1 }[/math], fall into two sets according to whether [math]\displaystyle{ \Delta \Im =+1 }[/math] or [math]\displaystyle{ \Delta \Im =-1 }[/math]. The set corresponding to [math]\displaystyle{ \Delta \Im =+1 }[/math] is called the R branch. The corresponding frequencies are given by: [math]\displaystyle{ \hbar {{\omega }^{R}}=E(v+1,\Im +1)-E(v,\Im)=2B(\Im +1)+\hbar {{\omega }_{0}};\text{ }\Im =0,1,2,...... }[/math]

The set corresponding to [math]\displaystyle{ \Delta \Im =-1 }[/math] is called the P branch. The corresponding frequencies are given by: [math]\displaystyle{ \hbar {{\omega }^{P}}=E(v+1,\Im -1)-E(v,\Im)=-2B\Im +\hbar {{\omega }_{0}};\text{ }\Im =1,2,3,...... }[/math]

Both branches make up what is called a rotational-vibrational band or a rovibrational band. These bands are in the infra-red part of the spectrum.

If the molecule is not in a [math]\displaystyle{ \Sigma }[/math] state, so that [math]\displaystyle{ \Lambda \ne 0 }[/math], transitions with [math]\displaystyle{ \Delta \Im =0 }[/math] are allowed. This gives rise to a further branch of the vibrational-rotational spectrum, called the Q branch. The frequencies [math]\displaystyle{ {{\omega }^{Q}} }[/math] corresponding to the lines in this branch are given by a quadratic function of [math]\displaystyle{ \Im }[/math] if [math]\displaystyle{ {{B}_{v}} }[/math] and [math]\displaystyle{ {{B}_{v+1}} }[/math] are unequal, and reduce to the single frequency: [math]\displaystyle{ \hbar {{\omega }^{Q}}=E(v+1,\Im)-E(v,\Im)=\hbar {{\omega }_{0}} }[/math] if [math]\displaystyle{ {{B}_{v+1}}={{B}_{v}} }[/math].

For a heteronuclear diatomic molecule, this selection rule has two consequences:

1. Both the vibrational and rotational quantum numbers must change. The Q-branch is therefore forbidden.
2. The energy change of rotation can be either subtracted from or added to the energy change of vibration, giving the P- and R- branches of the spectrum, respectively.

Homonuclear diatomic molecules also show this kind of spectra. The selection rules, however, are a bit different.

• Conclusion: Both homo- and hetero-nuclear diatomic molecules show rovibrational spectra. A Q-branch is absent in the spectra of heteronuclear diatomic molecules.

A special example: Hydrogen molecule ion

An explicit implication of symmetry on the molecular structure can be shown in case of the simplest bi-nuclear system: a hydrogen molecule ion or a di-hydrogen cation, [math]\displaystyle{ \text{H}_{2}^{+} }[/math]. A natural trial wave function for the [math]\displaystyle{ \text{H}_{2}^{+} }[/math] is determined by first considering the lowest-energy state of the system when the two protons are widely separated. Then there are clearly two possible states: the electron is attached either to one of the protons, forming a hydrogen atom in the ground state, or the electron is attached to the other proton, again in the ground state of a hydrogen atom (as depicted in the picture).

Two possible initial states of the system

The trial states in the position basis (or the 'wave functions') are then:

[math]\displaystyle{ \left\langle \mathbf{r}|\mathbf{1} \right\rangle =\frac{1}{\sqrt{\pi a_{0}^{3}}}{{e}^{-\frac{\left| \mathbf{r}-\frac{\mathbf{R}}{2} \right|}{{{a}_{0}}}}} }[/math] and [math]\displaystyle{ \left\langle \mathbf{r}|\mathbf{2} \right\rangle =\frac{1}{\sqrt{\pi a_{0}^{3}}}{{e}^{-\frac{\left| \mathbf{r}+\frac{\mathbf{R}}{2} \right|}{{{a}_{0}}}}} }[/math]

The analysis of [math]\displaystyle{ \text{H}_{2}^{+} }[/math] using variational method starts assuming these forms. Again, this is only one possible combination of states. There can be other combination of states also, for example, the electron is in an excited state of the hydrogen atom. The corresponding Hamiltonian of the system is:

[math]\displaystyle{ H=\frac{{{\mathbf{p}}^{2}}}{2{{m}_{e}}}-\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}-\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}+\frac{{{e}^{2}}}{R} }[/math]

Clearly, using the states [math]\displaystyle{ \left| 1 \right\rangle }[/math] and [math]\displaystyle{ \left| 2 \right\rangle }[/math] as basis will introduce off-diagonal elements in the Hamiltonian. Here, because of the relative simplicity of the [math]\displaystyle{ \text{H}_{2}^{+} }[/math] ion, the matrix elements can actually be calculated. The electronic Hamiltonian of [math]\displaystyle{ \text{H}_{2}^{+} }[/math] commutes with the point group inversion symmetry operation i. Using its symmetry properties, we can relate the diagonal and off-diagonal elements of the Hamiltonian as:

[math]\displaystyle{ {{H}_{11}}={{H}_{22}}\text{ and }{{H}_{12}}={{H}_{21}} }[/math]

The diagonal terms: [math]\displaystyle{ {{H}_{11}}=\left\langle 1|\frac{{{\mathbf{p}}^{2}}}{2{{m}_{e}}}-\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}|1 \right\rangle -\left\langle 1|\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}|1 \right\rangle +\frac{{{e}^{2}}}{R}\left\langle 1|1 \right\rangle }[/math][math]\displaystyle{ \Rightarrow {{H}_{11}}={{E}_{1}}-\int{{{d}^{3}}r}\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}{{\left| \left\langle \mathbf{r}|1 \right\rangle \right|}^{2}}+\frac{{{e}^{2}}}{R} }[/math][math]\displaystyle{ \Rightarrow {{H}_{11}}={{E}_{1}}-\int{{{d}^{3}}r}\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}{{\left| \left\langle \mathbf{r}|1 \right\rangle \right|}^{2}}+\frac{{{e}^{2}}}{R} }[/math] Where, [math]\displaystyle{ {{E}_{1}} }[/math]is the ground-state energy of the hydrogen atom. Again,[math]\displaystyle{ {{H}_{22}}=\left\langle 2|\frac{{{\mathbf{p}}^{2}}}{2{{m}_{e}}}-\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}|2 \right\rangle -\left\langle 2|\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}|2 \right\rangle +\frac{{{e}^{2}}}{R}\left\langle 2|2 \right\rangle }[/math] [math]\displaystyle{ \Rightarrow {{H}_{22}}={{E}_{1}}-\int{{{d}^{3}}r}\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}{{\left| \left\langle \mathbf{r}|2 \right\rangle \right|}^{2}}+\frac{{{e}^{2}}}{R}={{H}_{11}} }[/math] where the last step follows from the fact that [math]\displaystyle{ {{\left| \left\langle \mathbf{r}|2 \right\rangle \right|}^{2}}={{\left| \left\langle \mathbf{r}|1 \right\rangle \right|}^{2}}=\frac{1}{\pi a_{0}^{3}} }[/math] and from the symmetry of the system, the value of the integrals are same. Now the off-diagonal terms: [math]\displaystyle{ {{H}_{12}}=\left\langle 1|\frac{{{\mathbf{p}}^{2}}}{2{{m}_{e}}}-\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}|2 \right\rangle -\left\langle 1|\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}|2 \right\rangle +\frac{{{e}^{2}}}{R}\left\langle 1|2 \right\rangle }[/math] [math]\displaystyle{ \Rightarrow {{H}_{12}}=({{E}_{1}}+\frac{{{e}^{2}}}{R})\left\langle 1|2 \right\rangle -\int{{{d}^{3}}r}\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}\left\langle 1\left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \right|2 \right\rangle }[/math] by inserting a complete set of states [math]\displaystyle{ \int{{{d}^{3}}r}\left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \right| }[/math] in the last term. [math]\displaystyle{ \left\langle 1|2 \right\rangle =\int{{{d}^{3}}r}\left\langle 1\left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \right|2 \right\rangle }[/math] is called the 'overlap integral' And, [math]\displaystyle{ {{H}_{21}}=\left\langle 2|\frac{{{\mathbf{p}}^{2}}}{2{{m}_{e}}}-\frac{{{e}^{2}}}{\left| \mathbf{r}-\mathbf{R}/2 \right|}|1 \right\rangle -\left\langle 2|\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}|1 \right\rangle +\frac{{{e}^{2}}}{R}\left\langle 2|1 \right\rangle }[/math] [math]\displaystyle{ \Rightarrow {{H}_{21}}=({{E}_{1}}+\frac{{{e}^{2}}}{R})\left\langle 2|1 \right\rangle -\int{{{d}^{3}}r}\frac{{{e}^{2}}}{\left| \mathbf{r}+\mathbf{R}/2 \right|}\left\langle 2\left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \right|1 \right\rangle ={{H}_{12}} }[/math] (as the wave functions are real) So, [math]\displaystyle{ {{H}_{11}}={{H}_{22}}\text{ and }{{H}_{12}}={{H}_{21}} }[/math]

Because [math]\displaystyle{ {{H}_{11}}={{H}_{22}} }[/math] as well as [math]\displaystyle{ {{H}_{12}}={{H}_{21}} }[/math], the linear combination of [math]\displaystyle{ \left| 1 \right\rangle }[/math] and[math]\displaystyle{ \left| 2 \right\rangle }[/math] that diagonalizes the Hamiltonian is [math]\displaystyle{ \left| \pm \right\rangle =\frac{1}{\sqrt{2\pm 2\left\langle 1|2 \right\rangle }}(\left| 1 \right\rangle \pm \left| 2 \right\rangle) }[/math] (after normalization). Now as [math]\displaystyle{ [H, }[/math]i[math]\displaystyle{ ]=0 }[/math] for [math]\displaystyle{ \text{H}_{2}^{+} }[/math], the states [math]\displaystyle{ \left| \pm \right\rangle }[/math] are also eigenstates of i. It turns out that [math]\displaystyle{ \left| + \right\rangle }[/math] and [math]\displaystyle{ \left| - \right\rangle }[/math] are the eigenstates of i with eigenvalues +1 and -1 (in other words, the wave functions [math]\displaystyle{ \left\langle \mathbf{r}|+ \right\rangle }[/math] and [math]\displaystyle{ \left\langle \mathbf{r}|- \right\rangle }[/math] are gerade (symmetric) and ungerade (unsymmetric), respectively). The corresponding expectation value of the energies are [math]\displaystyle{ {{E}_{\pm }}=\frac{1}{1\pm \left\langle 1|2 \right\rangle }({{H}_{11}}\pm {{H}_{12}}) }[/math].

The energy vs separation graphs of [math]\displaystyle{ \text{H}_{2}^{+} }[/math]. The two lowest curves denote the [math]\displaystyle{ {{E}_{-}} }[/math] and [math]\displaystyle{ {{E}_{+}} }[/math] states respectively. Higher ones are the excited states. The minimum of [math]\displaystyle{ {{E}_{+}} }[/math] corresponds to an energy [math]\displaystyle{ -15.4 \text{ eV} }[/math]

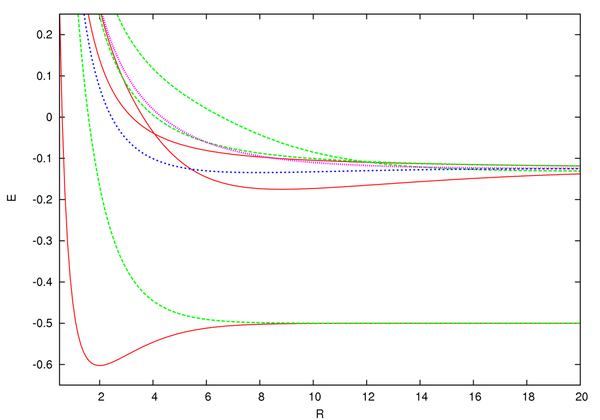
From the graph, we see that only [math]\displaystyle{ {{E}_{+}} }[/math] has a minimum corresponding to a separation of 1.3 Å and a total energy [math]\displaystyle{ {{E}_{+}}=-15.4 \text{ eV} }[/math], which is less than the initial energy of the system, [math]\displaystyle{ -13.6 \text{ eV} }[/math]. Thus, only the gerade state stabilizes the ion with a binding energy of [math]\displaystyle{ 1.8 \text{ eV} }[/math]. As a result, the ground state of [math]\displaystyle{ \text{H}_{2}^{+} }[/math] is [math]\displaystyle{ {{X}^{2}}\Sigma _{g}^{+} }[/math] and this state [math]\displaystyle{ \left(\left| + \right\rangle \right) }[/math] is called a bonding molecular orbital.

Thus, symmetry plays an explicit role in the formation of [math]\displaystyle{ \text{H}_{2}^{+} }[/math].

See also

• Character table
• Irreducible representation § Applications in theoretical physics and chemistry
• Parity (physics) § Molecules
• Diatomic molecule
• Molecular symmetry
• Schoenflies notation
• List of character tables for chemically important 3D point groups
• Hund's cases
• Rotational-vibrational spectroscopy
• Molecular term symbol
• Avoided crossing
• Dihydrogen cation
• Symmetry in quantum mechanics
• Group (mathematics)
• Point groups in three dimensions
• Complete set of commuting observables
• Born-Oppenheimer approximation

Further reading

1. Quantum Mechanics, Third Edition: Non-Relativistic Theory (Volume 3)by L. D. Landau, L. M. Lifshitz; ISBN:978-0750635394 Edition: 3rd; chapters: XI and XII.
2. Physics of Atoms & Molecules by B.H. Bransden, C.J. Joachain; ISBN:978-8177582796 Edition: 2nd edition; chapter: 9
3. Molecular Spectra and Molecular Structure: Spectra of Diatomic Molecules by Gerhard Herzberg; ISBN:978-0894642685 Edition: 2nd
4. Molecular Quantum Mechanics by Peter W. Atkins, Ronald S. Friedman; ISBN:978-0199541423 Edition: 5th; chapter: 10.
5. Lecture notes on Quantum Mechanics (handouts: 12, 10) by Prof. Sourendu Gupta, Tata Institute of Fundamental Research, Mumbai.
6. Symmetry in Physics: Principles and Simple Applications Volume 1 by James Philip Elliott, P.G. Dawber; ISBN:978-0195204551
7. A Modern Approach to Quantum Mechanics by John S. Townsend; Edition 2nd; ISBN:978-1891389788
8. http://www.astro.uwo.ca/~jlandstr/p467/lec5-mol_spect/index.html

External links

1. http://www.astro.uwo.ca/~jlandstr/p467/lec5-mol_spect/index.html
2. http://csi.chemie.tu-darmstadt.de/ak/immel/script/redirect.cgi?filename=http://csi.chemie.tu-darmstadt.de/ak/immel/tutorials/symmetry/index1.html
3. http://theory.tifr.res.in/~sgupta/courses/qm2014/index.php
4. A pdf file explaining the relation between Point Groups and Permutation-Inversion Groups Link