Non-abelian group
| Algebraic structure → Group theory Group theory |
|---|
 |
In mathematics, and specifically in group theory, a non-abelian group, sometimes called a non-commutative group, is a group (G, ∗) in which there exists at least one pair of elements a and b of G, such that a ∗ b ≠ b ∗ a.[1][2] This class of groups contrasts with the abelian groups, where all pairs of group elements commute.
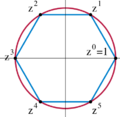
Non-abelian groups are pervasive in mathematics and physics. One of the simplest examples of a non-abelian group is the dihedral group of order 6. It is the smallest finite non-abelian group. A common example from physics is the rotation group SO(3) in three dimensions (for example, rotating something 90 degrees along one axis and then 90 degrees along a different axis is not the same as doing them in reverse order).
Both discrete groups and continuous groups may be non-abelian. Most of the interesting Lie groups are non-abelian, and these play an important role in gauge theory.
See also
References
- ↑ Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra (3rd ed.). John Wiley & Sons. ISBN 0-471-43334-9.
- ↑ Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. Springer. ISBN 0-387-95385-X.
 |

