Clairaut's equation (mathematical analysis)
| Differential equations |
|---|
 |
| Classification |
| Solution |
In mathematical analysis, Clairaut's equation (or the Clairaut equation) is a differential equation of the form
where f is continuously differentiable. It is a particular case of the Lagrange differential equation. It is named after the French mathematician Alexis Clairaut, who introduced it in 1734.[1]
Definition
To solve Clairaut's equation, one differentiates with respect to x, yielding
so
Hence, either
or
In the former case, C = dy/dx for some constant C. Substituting this into the Clairaut's equation, one obtains the family of straight line functions given by
the so-called general solution of Clairaut's equation.
The latter case,
defines only one solution y(x), the so-called singular solution, whose graph is the envelope of the graphs of the general solutions. The singular solution is usually represented using parametric notation, as (x(p), y(p)), where p = dy/dx.
The parametric description of the singular solution has the form
where t is a parameter.
Examples
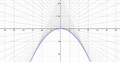
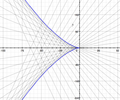
The following curves represent the solutions to two Clairaut's equations:
In each case, the general solutions are depicted in black while the singular solution is in violet.
Extension
By extension, a first-order partial differential equation of the form
is also known as Clairaut's equation.[2]
See also
Notes
References
- Clairaut, Alexis Claude (1734), "Solution de plusieurs problèmes où il s'agit de trouver des Courbes dont la propriété consiste dans une certaine relation entre leurs branches, exprimée par une Équation donnée.", Histoire de l'Académie royale des sciences: 196–215, http://gallica.bnf.fr/ark:/12148/bpt6k3531x/f344.table.
- Kamke, E. (1944) (in de), Differentialgleichungen: Lösungen und Lösungsmethoden, 2. Partielle Differentialgleichungen 1er Ordnung für eine gesuchte Funktion, Akad. Verlagsgesell.
- Hazewinkel, Michiel, ed. (2001), "Clairaut equation", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=C/c022350.