Compound of two tetrahedra
In geometry, a compound of two tetrahedra is constructed by two overlapping tetrahedra, usually implied as regular tetrahedra.
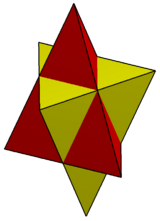
Stellated octahedron
There is only one uniform polyhedral compound, the stellated octahedron, which has octahedral symmetry, order 48. It has a regular octahedron core, and shares the same 8 vertices with the cube.
If the edge crossings were treated as their own vertices, the compound would have identical surface topology to the rhombic dodecahedron; were face crossings also considered edges of their own the shape would effectively become a nonconvex triakis octahedron.
|
A tetrahedron and its dual tetrahedron |
|
|
Orthographic projections from the different symmetry axes |
If the edge crossings were vertices, the mapping on a sphere would be the same as that of a rhombic dodecahedron. |
Lower symmetry constructions
There are lower symmetry variations on this compound, based on lower symmetry forms of the tetrahedron.
- A facetting of a rectangular cuboid, creating compounds of two tetragonal or two rhombic disphenoids, with a bipyramid or rhombic fusil cores. This is first in a set of uniform compound of two antiprisms.
- A facetting of a trigonal trapezohedron creates a compound of two right triangular pyramids with a triangular antiprism core. This is first in a set of compounds of two pyramids positioned as point reflections of each other.
| D4h, [4,2], order 16 | C4v, [4], order 8 | D3d, [2+,6], order 12 |
|---|---|---|
 Compound of two tetragonal disphenoids in square prism ß{2,4} or    
|
 Compound of two digonal disphenoids |
 Compound of two right triangular pyramids in triangular trapezohedron |
Other compounds
If two regular tetrahedra are given the same orientation on the 3-fold axis, a different compound is made, with D3h, [3,2] symmetry, order 12.
Other orientations can be chosen as 2 tetrahedra within the compound of five tetrahedra and compound of ten tetrahedra the latter of which can be seen as a hexagrammic pyramid:
See also
- Compound of cube and octahedron
- Compound of dodecahedron and icosahedron
- Compound of small stellated dodecahedron and great dodecahedron
- Compound of great stellated dodecahedron and great icosahedron
References
- Cundy, H. and Rollett, A. "Five Tetrahedra in a Dodecahedron". §3.10.8 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 139–141, 1989.
External links
- Weisstein, Eric W.. "Compound of two tetrahedra". http://mathworld.wolfram.com/Tetrahedron2-Compound.html.
- Compounds of Polyhedra VRML model: [1]
 |  |
