Shor's algorithm

Short description: Quantum algorithm for integer factorization

Shor's algorithm is a quantum algorithm for finding the prime factors of an integer. It was developed in 1994 by the American mathematician Peter Shor. It is one of the few known quantum algorithms with compelling potential applications and strong evidence of superpolynomial speedup compared to best known classical (that is, non-quantum) algorithms. On the other hand, factoring numbers of practical significance requires far more qubits than available in the near future. Another concern is that noise in quantum circuits may undermine results, requiring additional qubits for quantum error correction.

Shor proposed multiple similar algorithms solving the factoring problem, the discrete logarithm problem, and the period finding problem. "Shor's algorithm" usually refers to his algorithm solving factoring, but may also refer to each of the three. The discrete logarithm algorithm and the factoring algorithm are instances of the period finding algorithm, and all three are instances of the hidden subgroup problem.

On a quantum computer, to factor an integer [math]\displaystyle{ N }[/math], Shor's algorithm runs in polynomial time, meaning the time taken is polynomial in [math]\displaystyle{ \log N }[/math], the size of the integer given as input. Specifically, it takes quantum gates of order [math]\displaystyle{ O \! \left((\log N)^{2} (\log \log N) (\log \log \log N) \right) }[/math] using fast multiplication, or even [math]\displaystyle{ O \! \left((\log N)^{2} (\log \log N) \right) }[/math] utilizing the asymptotically fastest multiplication algorithm currently known due to Harvey and Van Der Hoven, thus demonstrating that the integer factorization problem can be efficiently solved on a quantum computer and is consequently in the complexity class BQP. This is significantly faster than the most efficient known classical factoring algorithm, the general number field sieve, which works in sub-exponential time: [math]\displaystyle{ O \! \left(e^{1.9 (\log N)^{1/3} (\log \log N)^{2/3}} \right) }[/math].

Feasibility and impact

If a quantum computer with a sufficient number of qubits could operate without succumbing to quantum noise and other quantum-decoherence phenomena, then Shor's algorithm could be used to break public-key cryptography schemes, such as

• The RSA scheme
• The Finite Field Diffie-Hellman key exchange
• The Elliptic Curve Diffie-Hellman key exchange

RSA is based on the assumption that factoring large integers is computationally intractable. As far as is known, this assumption is valid for classical (non-quantum) computers; no classical algorithm is known that can factor integers in polynomial time. However, Shor's algorithm shows that factoring integers is efficient on an ideal quantum computer, so it may be feasible to defeat RSA by constructing a large quantum computer. It was also a powerful motivator for the design and construction of quantum computers, and for the study of new quantum-computer algorithms. It has also facilitated research on new cryptosystems that are secure from quantum computers, collectively called post-quantum cryptography.

Physical implementation

Given the high error rates of contemporary quantum computers and too few qubits to use quantum error correction, laboratory demonstrations obtain correct results only in a fraction of attempts.

In 2001, Shor's algorithm was demonstrated by a group at IBM, who factored [math]\displaystyle{ 15 }[/math] into [math]\displaystyle{ 3 \times 5 }[/math], using an NMR implementation of a quantum computer with seven qubits. After IBM's implementation, two independent groups implemented Shor's algorithm using photonic qubits, emphasizing that multi-qubit entanglement was observed when running the Shor's algorithm circuits. In 2012, the factorization of [math]\displaystyle{ 15 }[/math] was performed with solid-state qubits. Later, in 2012, the factorization of [math]\displaystyle{ 21 }[/math] was achieved. In 2019, an attempt was made to factor the number [math]\displaystyle{ 35 }[/math] using Shor's algorithm on an IBM Q System One, but the algorithm failed because of accumulating errors. Though larger numbers have been factored by quantum computers using other algorithms, these algorithms are similar to classical brute-force checking of factors, so unlike Shor's algorithm, they are not expected to ever perform better than classical factoring algorithms.

Theoretical analyses of Shor's algorithm assume a quantum computer free of noise and errors. However, near-term practical implementations will have to deal with such undesired phenomena (when more qubits are available, Quantum error correction can help). In 2023, Jin-Yi Cai studied the impact of noise and concluded that there is a special class of numbers (products of two primes from A073024, which are dense in the semiprimes), Shor's algorithm cannot factor such numbers in the presence of noise. Hence error-correction will be needed to be able to factor all numbers with Shor's algorithm.

Algorithm

The problem that we are trying to solve is: given an odd composite number [math]\displaystyle{ N }[/math], find its integer factors.

To achieve this, Shor's algorithm consists of two parts:

1. A classical reduction of the factoring problem to the problem of order-finding. This reduction is similar to that used for other factoring algorithms, such as the quadratic sieve.
2. A quantum algorithm to solve the order-finding problem.

Classical reduction

A complete factoring algorithm is possible if we're able to efficiently factor arbitrary [math]\displaystyle{ N }[/math] into just two integers [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] greater than 1, since if either [math]\displaystyle{ p }[/math] or [math]\displaystyle{ q }[/math] are not prime then the factoring algorithm can in turn be run on those until only primes remain.

A basic observation is that, using Euclid's algorithm, we can always compute the GCD between two integers efficiently. In particular, this means we can check efficiently whether [math]\displaystyle{ N }[/math] is even, in which case 2 is trivially a factor. Let us thus assume that [math]\displaystyle{ N }[/math] is odd for the remainder of this discussion. Afterwards, we can use efficient classical algorithms to check if [math]\displaystyle{ N }[/math] is a prime power. For prime powers, efficient classical factorization algorithms exist, hence the rest of the quantum algorithm may assume that [math]\displaystyle{ N }[/math] is not a prime power.

If those easy cases do not produce a nontrivial factor of [math]\displaystyle{ N }[/math], the algorithm proceeds to handle the remaining case. We pick a random integer [math]\displaystyle{ 2 \leq a \lt N }[/math]. A possible nontrivial divisor of [math]\displaystyle{ N }[/math] can be found by computing [math]\displaystyle{ \gcd(a, N) }[/math], which can be done classically and efficiently using the Euclidean algorithm. If this produces a nontrivial factor (meaning [math]\displaystyle{ \gcd(a, N) \ne 1 }[/math]), the algorithm is finished, and the other nontrivial factor is [math]\displaystyle{ \frac{N}{\gcd(a,N)} }[/math]. If a nontrivial factor was not identified, then that means that [math]\displaystyle{ N }[/math] and the choice of [math]\displaystyle{ a }[/math] are coprime. Here, the algorithm runs the quantum subroutine, which will return the order [math]\displaystyle{ r }[/math] of [math]\displaystyle{ a }[/math], meaning

[math]\displaystyle{ a^{r} \equiv 1 \bmod N. }[/math]

The quantum subroutine requires that [math]\displaystyle{ a }[/math] and [math]\displaystyle{ N }[/math] are coprime, which is true since at this point in the algorithm, [math]\displaystyle{ \gcd(a, N) }[/math] did not produce a nontrivial factor of [math]\displaystyle{ N }[/math]. It can be seen from the congruence that [math]\displaystyle{ N }[/math] divides [math]\displaystyle{ a^{r} - 1 }[/math], written [math]\displaystyle{ N \mid a^{r} - 1 }[/math]. This can be factored using difference of squares:[math]\displaystyle{ N \mid (a^{r/2} - 1)(a^{r/2} + 1) }[/math] Since we have factored the expression in this way, the algorithm doesn't work for odd [math]\displaystyle{ r }[/math] (because [math]\displaystyle{ a^{r/2} }[/math] must be an integer), meaning the algorithm would have to restart with a new [math]\displaystyle{ a }[/math]. Hereafter we can therefore assume [math]\displaystyle{ r }[/math] is even. It cannot be the case that [math]\displaystyle{ N \mid a^{r/2} - 1 }[/math], since this would imply [math]\displaystyle{ a^{r/2} \equiv 1 \bmod N }[/math], which would contradictorily imply that [math]\displaystyle{ \frac{r}{2} }[/math] would be the order of [math]\displaystyle{ a }[/math], which was already [math]\displaystyle{ r }[/math]. At this point, it may or may not be the case that [math]\displaystyle{ N \mid a^{r/2} + 1 }[/math]. If it is not true that [math]\displaystyle{ N \mid a^{r/2} + 1 }[/math], then that means we are able to find a nontrivial factor of [math]\displaystyle{ N }[/math]. We compute[math]\displaystyle{ d = \gcd(N, a^{r/2} - 1) }[/math]If [math]\displaystyle{ d = 1 }[/math], then that means [math]\displaystyle{ N \mid a^{r/2} + 1 }[/math] was true, and a nontrivial factor of [math]\displaystyle{ N }[/math] cannot be achieved from [math]\displaystyle{ a }[/math], and the algorithm must restart with a new [math]\displaystyle{ a }[/math]. Otherwise, we have found a nontrivial factor of [math]\displaystyle{ N }[/math], with the other being [math]\displaystyle{ \frac{N}{d} }[/math], and the algorithm is finished. For this step, it is also equivalent to compute [math]\displaystyle{ \gcd(N, a^{r/2} + 1) }[/math]; it will produce a nontrivial factor if [math]\displaystyle{ \gcd(N, a^{r/2} - 1) }[/math] is nontrivial, and will not if it's trivial (where [math]\displaystyle{ N \mid a^{r/2} + 1 }[/math]).

The algorithm restated shortly follows: let [math]\displaystyle{ N }[/math] be odd, and not a prime power. We want to output two nontrivial factors of [math]\displaystyle{ N }[/math].

1. Pick a random number [math]\displaystyle{ 1 \lt a \lt N }[/math].
2. Compute [math]\displaystyle{ K=\gcd(a,N) }[/math], the greatest common divisor of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ N }[/math].
3. If [math]\displaystyle{ K \neq 1 }[/math], then [math]\displaystyle{ K }[/math] is a nontrivial factor of [math]\displaystyle{ N }[/math], with the other factor being [math]\displaystyle{ \frac{N}{K} }[/math] and we are done.
4. Otherwise, use the quantum subroutine to find the order [math]\displaystyle{ r }[/math] of [math]\displaystyle{ a }[/math].
5. If [math]\displaystyle{ r }[/math] is odd, then go back to step 1.
6. Compute [math]\displaystyle{ g = \gcd(N, a^{r/2} + 1) }[/math]. If [math]\displaystyle{ g }[/math] is nontrivial, the other factor is [math]\displaystyle{ \frac{N}{g} }[/math], and we're done. Otherwise, go back to step 1.

It has been shown that this will be likely to succeed after a few runs. In practice, a single call to the quantum order-finding subroutine is enough to completely factor [math]\displaystyle{ N }[/math] with very high probability of success if one uses a more advanced reduction.

Quantum order-finding subroutine

The goal of the quantum subroutine of Shor's algorithm is, given coprime integers [math]\displaystyle{ N }[/math] and [math]\displaystyle{ 1\lt a\lt N }[/math], to find the order [math]\displaystyle{ r }[/math] of [math]\displaystyle{ a }[/math] modulo [math]\displaystyle{ N }[/math], which is the smallest positive integer such that [math]\displaystyle{ a^r \equiv 1 \pmod N }[/math]. To achieve this, Shor's algorithm uses a quantum circuit involving two registers. The second register uses [math]\displaystyle{ n }[/math] qubits, where [math]\displaystyle{ n }[/math] is the smallest integer such that [math]\displaystyle{ N\le 2^n }[/math]. The size of the first register determines how accurate of an approximation the circuit produces. It can be shown that using [math]\displaystyle{ 2n + 1 }[/math] qubits gives sufficient accuracy to find [math]\displaystyle{ r }[/math]. The exact quantum circuit depends on the parameters [math]\displaystyle{ a }[/math] and [math]\displaystyle{ N }[/math], which define the problem. The following description of the algorithm uses bra–ket notation to denote quantum states, and [math]\displaystyle{ \otimes }[/math] to denote the tensor product, rather than logical OR or logical XOR.

The algorithm consists of two main steps:

1. Use quantum phase estimation with unitary [math]\displaystyle{ U }[/math] representing the operation of multiplying by [math]\displaystyle{ a }[/math] (modulo [math]\displaystyle{ N }[/math]), and input state [math]\displaystyle{ |0\rangle^{\otimes 2 n + 1}\otimes|1\rangle }[/math] (where the second register is [math]\displaystyle{ |1\rangle }[/math] made from [math]\displaystyle{ n }[/math] qubits). The eigenvalues of this [math]\displaystyle{ U }[/math] encode information about the period, and [math]\displaystyle{ |1\rangle }[/math] can be seen to be writable as a sum of its eigenvectors. Thanks to these properties, the quantum phase estimation stage gives as output a random integer of the form [math]\displaystyle{ \frac{j}{r} 2^{2n + 1} }[/math] for random [math]\displaystyle{ j=0,1,...,r-1 }[/math].
2. Use the continued fractions algorithm to extract the period [math]\displaystyle{ r }[/math] from the measurement outcomes obtained in the previous stage. This is a procedure to post-process (with a classical computer) the measurement data obtained from measuring the output quantum states, and retrieve the period.

The connection with quantum phase estimation was not discussed in the original formulation of Shor's algorithm, but was later proposed by Kitaev.

Quantum phase estimation

Quantum subroutine in Shor's algorithm

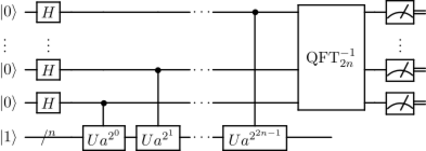
In general the quantum phase estimation algorithm, for any unitary [math]\displaystyle{ U }[/math] and eigenstate [math]\displaystyle{ |\psi\rangle }[/math] such that [math]\displaystyle{ U|\psi\rangle=e^{2\pi i\theta} |\psi\rangle }[/math], sends inputs states [math]\displaystyle{ |0\rangle|\psi\rangle }[/math] into output states close to [math]\displaystyle{ |\phi\rangle|\psi\rangle }[/math], where [math]\displaystyle{ \phi }[/math] is an integer close to [math]\displaystyle{ 2^{2n + 1} \theta }[/math]. In other words, it sends each eigenstate [math]\displaystyle{ |\psi_j\rangle }[/math] of [math]\displaystyle{ U }[/math] into a state close to the associated eigenvalue. For the purposes of quantum order-finding, we employ this strategy using the unitary defined by the action[math]\displaystyle{ U|k\rangle = \begin{cases} |ak \pmod N\rangle & 0 \le k \lt N, \\ |k\rangle & N \le k \lt 2^n.\end{cases} }[/math]The action of [math]\displaystyle{ U }[/math] on states [math]\displaystyle{ |k\rangle }[/math] with [math]\displaystyle{ N \leq k \lt 2^n }[/math] is not crucial to the functioning of the algorithm, but needs to be included to ensure the overall transformation is a well-defined quantum gate. Implementing the circuit for quantum phase estimation with [math]\displaystyle{ U }[/math] requires being able to efficiently implement the gates [math]\displaystyle{ U^{2^j} }[/math]. This can be accomplished via modular exponentiation, which is the slowest part of the algorithm. The gate thus defined satisfies [math]\displaystyle{ U^r=I }[/math], which immediately implies that its eigenvalues are the [math]\displaystyle{ r }[/math]-th roots of unity [math]\displaystyle{ \omega_r^k=e^{2\pi ik/r} }[/math]. Furthermore, each eigenvalue [math]\displaystyle{ \omega_r^k }[/math] has an eigenvector of the form [math]\displaystyle{ |\psi_j\rangle=r^{-1/2}\sum_{k=0}^{r-1}\omega_r^{-kj}|a^k\rangle }[/math], and these eigenvectors are such that[math]\displaystyle{ \begin{align} \frac{1}{\sqrt{r}} \sum_{j = 0}^{r - 1} |\psi_j\rangle &= \frac{1}{r} \sum_{j = 0}^{r - 1} \sum_{k = 0}^{r - 1} \omega_r^{jk}|a^k\rangle \\ &= |1\rangle + \frac{1}{r} \sum_{k = 1}^{r - 1} \left(\sum_{j = 0}^{r - 1} \omega_r^{jk} \right) |a^k\rangle =|1\rangle, \end{align} }[/math]

where the last identity follows from the geometric series formula, which implies [math]\displaystyle{ \sum_{j = 0}^{r - 1} \omega_r^{jk} = 0 }[/math].

Using quantum phase estimation on an input state [math]\displaystyle{ |0\rangle^{\otimes 2 n + 1}|\psi_j\rangle }[/math] would then return the integer [math]\displaystyle{ 2^{2n + 1} j/r }[/math] with high probability. More precisely, the quantum phase estimation circuit sends [math]\displaystyle{ |0\rangle^{\otimes 2 n + 1}|\psi_j\rangle }[/math] to [math]\displaystyle{ |\phi_j\rangle|\psi_j\rangle }[/math] such that the resulting probability distribution [math]\displaystyle{ p_k \equiv|\langle k|\phi_j\rangle|^2 }[/math] is peaked around [math]\displaystyle{ k=2^{2n + 1} j/r }[/math], with [math]\displaystyle{ p_{2^{2n+1}j/r}\ge \frac{4}{\pi^2} \approx 0.4053 }[/math]. This probability can be made arbitrarily close to 1 using extra qubits.

Applying the above reasoning to the input [math]\displaystyle{ |0\rangle^{\otimes 2 n + 1}|1\rangle }[/math], quantum phase estimation thus results in the evolution[math]\displaystyle{ |0\rangle^{\otimes 2 n}|1\rangle = \frac{1}{\sqrt{r}} \sum_{j = 0}^{r - 1} |0\rangle^{\otimes 2 n} |\psi_j\rangle \to \frac{1}{\sqrt{r}} \sum_{j = 0}^{r - 1} |\phi_j\rangle|\psi_j\rangle. }[/math]Measuring the first register, we now have a balanced probability [math]\displaystyle{ 1/r }[/math] to find each [math]\displaystyle{ |\phi_j\rangle }[/math], each one giving an integer approximation to [math]\displaystyle{ 2^{2 n + 1} j/r }[/math], which can be divided by [math]\displaystyle{ 2^{2n + 1} }[/math] to get a decimal approximation for [math]\displaystyle{ j/r }[/math].

Continued fraction algorithm to retrieve the period

Then, we apply the continued fractions algorithm to find integers [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math], where [math]\displaystyle{ \frac{b}{c} }[/math] gives the best fraction approximation for the approximation measured from the circuit, for [math]\displaystyle{ b, c \lt N }[/math] and coprime [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math]. The number of qubits in the first register, [math]\displaystyle{ 2n + 1 }[/math], which determines the accuracy of the approximation, guarantees that[math]\displaystyle{ \frac{b}{c} = \frac{j}{r} }[/math]given the best approximation from the superposition of [math]\displaystyle{ |\phi_j\rangle }[/math] was measured (which can be made arbitrarily likely by using extra bits and truncating the output). However, while [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] are coprime, it may be the case that [math]\displaystyle{ j }[/math] and [math]\displaystyle{ r }[/math] are not coprime. Because of that, [math]\displaystyle{ b }[/math] and [math]\displaystyle{ c }[/math] may have lost some factors that were in [math]\displaystyle{ j }[/math] and [math]\displaystyle{ r }[/math]. This can be remedied by rerunning the quantum subroutine an arbitrary number of times, to produce a list of fraction approximations[math]\displaystyle{ \frac{b_1}{c_1}_{\textstyle ,} \; \frac{b_2}{c_2}_{\textstyle ,} \ldots \vphantom{\frac{b_1}{c_1}}_{\textstyle ,} \; \frac{b_s}{c_s} }[/math]where [math]\displaystyle{ s }[/math] is the number of times the algorithm was run. Each [math]\displaystyle{ c_k }[/math] will have different factors taken out of it because the circuit will (likely) have measured multiple different possible values of [math]\displaystyle{ j }[/math]. To recover the actual [math]\displaystyle{ r }[/math] value, we can take the least common multiple of each [math]\displaystyle{ c_k }[/math]:[math]\displaystyle{ \mathrm{lcm}(c_1, c_2, \ldots, c_s) }[/math]The least common multiple will be the order [math]\displaystyle{ r }[/math] of the original integer [math]\displaystyle{ a }[/math] with high probability.

Choosing the size of the first register

Phase estimation requires choosing the size of the first register to determine the accuracy of the algorithm, and for the quantum subroutine of Shor's algorithm, [math]\displaystyle{ 2n + 1 }[/math] qubits is sufficient to guarantee that the optimal bitstring measured from phase estimation (meaning the [math]\displaystyle{ |k\rangle }[/math] where [math]\displaystyle{ k / 2^{2n + 1} }[/math] is the most accurate approximation of the phase from phase estimation) will allow the actual value of [math]\displaystyle{ r }[/math] to be recovered.

Each [math]\displaystyle{ |\phi_j\rangle }[/math] before measurement in Shor's algorithm represents a superposition of integers approximating [math]\displaystyle{ 2^{2 n + 1} j/r }[/math]. Let [math]\displaystyle{ |k\rangle }[/math] represent the most optimal integer in [math]\displaystyle{ |\phi_j\rangle }[/math]. The following theorem guarantees that the continued fractions algorithm will recover [math]\displaystyle{ j/r }[/math] from [math]\displaystyle{ k/2^{2 {n} + 1} }[/math]:

Theorem — If [math]\displaystyle{ j }[/math] and [math]\displaystyle{ r }[/math] are [math]\displaystyle{ n }[/math] bit integers, and [math]\displaystyle{ \left\vert \frac{j}{r} - \phi\right\vert \leq \frac{1}{2 r^2} }[/math] then the continued fractions algorithm run on [math]\displaystyle{ \phi }[/math] will recover both [math]\displaystyle{ \frac{j}{\gcd(j,\; r)} }[/math] and [math]\displaystyle{ \frac{r}{\gcd(j,\; r)} }[/math].

As [math]\displaystyle{ k }[/math] is the optimal bitstring from phase estimation, [math]\displaystyle{ k/2^{2 {n} + 1} }[/math] is accurate to [math]\displaystyle{ j/r }[/math] by [math]\displaystyle{ 2n + 1 }[/math] bits. Thus,[math]\displaystyle{ \left\vert\frac{j}{r} - \frac{k}{2^{2n + 1}}\right\vert \leq \frac{1}{2^{2 {n} + 1}} \leq \frac{1}{2N^2} \leq \frac{1}{2r^2} }[/math]which implys that the continued fractions algorithm will recover [math]\displaystyle{ j }[/math] and [math]\displaystyle{ r }[/math] (or with their greatest common divisor taken out).

The bottleneck

The runtime bottleneck of Shor's algorithm is quantum modular exponentiation, which is by far slower than the quantum Fourier transform and classical pre-/post-processing. There are several approaches to constructing and optimizing circuits for modular exponentiation. The simplest and (currently) most practical approach is to mimic conventional arithmetic circuits with reversible gates, starting with ripple-carry adders. Knowing the base and the modulus of exponentiation facilitates further optimizations. Reversible circuits typically use on the order of [math]\displaystyle{ n^3 }[/math] gates for [math]\displaystyle{ n }[/math] qubits. Alternative techniques asymptotically improve gate counts by using quantum Fourier transforms, but are not competitive with fewer than 600 qubits owing to high constants.

Period finding and discrete logarithms

Shor's algorithms for the discrete log and the order finding problems are instances of an algorithm solving the period finding problem.. All three are instances of the hidden subgroup problem.

Shor's algorithm for discrete logarithms

Given a group [math]\displaystyle{ G }[/math] with order [math]\displaystyle{ p }[/math] and generator [math]\displaystyle{ g \in G }[/math], suppose we know that [math]\displaystyle{ x = g^{r} \in G }[/math], for some [math]\displaystyle{ r \in \mathbb{Z}_p }[/math], and we wish to compute [math]\displaystyle{ r }[/math], which is the discrete logarithm: [math]\displaystyle{ r = {\log_{g}}(x) }[/math]. Consider the abelian group [math]\displaystyle{ \mathbb{Z}_{p} \times \mathbb{Z}_{p} }[/math], where each factor corresponds to modular addition of values. Now, consider the function

[math]\displaystyle{ f \colon \mathbb{Z}_{p} \times \mathbb{Z}_{p} \to G \;;\; f(a,b) = g^{a} x^{- b} . }[/math]

This gives us an abelian hidden subgroup problem, where [math]\displaystyle{ f }[/math] corresponds to a group homomorphism. The kernel corresponds to the multiples of [math]\displaystyle{ (r,1) }[/math]. So, if we can find the kernel, we can find [math]\displaystyle{ r }[/math]. A quantum algorithm for solving this problem exists. This algorithm is, like the factor-finding algorithm, due to Peter Shor and both are implemented by creating a superposition through using Hadamard gates, followed by implementing [math]\displaystyle{ f }[/math] as a quantum transform, followed finally by a quantum Fourier transform. Due to this, the quantum algorithm for computing the discrete logarithm is also occasionally referred to as "Shor's Algorithm."

The order-finding problem can also be viewed as a hidden subgroup problem. To see this, consider the group of integers under addition, and for a given [math]\displaystyle{ a\in\mathbb{Z} }[/math] such that: [math]\displaystyle{ a^{r}=1 }[/math], the function

[math]\displaystyle{ f \colon \mathbb{Z}\to \mathbb{Z} \;;\; f(x) = a^{x},\; f(x+r) = f(x) . }[/math]

For any finite abelian group [math]\displaystyle{ G }[/math], a quantum algorithm exists for solving the hidden subgroup for [math]\displaystyle{ G }[/math] in polynomial time.

See also

• GEECM, a factorization algorithm said to be "often much faster than Shor's"
• Grover's algorithm

Further reading

• Nielsen, Michael A.; Chuang, Isaac L. (2010), Quantum Computation and Quantum Information, 10th Anniversary Edition, Cambridge University Press, ISBN 9781107002173 .
• Phillip Kaye, Raymond Laflamme, Michele Mosca, An introduction to quantum computing, Oxford University Press, 2007, ISBN 0-19-857049-X
• "Explanation for the man in the street" by Scott Aaronson, "approved" by Peter Shor. (Shor wrote "Great article, Scott! That’s the best job of explaining quantum computing to the man on the street that I’ve seen."). An alternate metaphor for the QFT was presented in one of the comments. Scott Aaronson suggests the following 12 references as further reading (out of "the 10¹⁰⁵⁰⁰⁰ quantum algorithm tutorials that are already on the web."):
• Shor, Peter W. (1997), "Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer", SIAM J. Comput. 26 (5): 1484–1509, doi:10.1137/S0036144598347011, Bibcode: 1999SIAMR..41..303S . Revised version of the original paper by Peter Shor ("28 pages, LaTeX. This is an expanded version of a paper that appeared in the Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, Nov. 20--22, 1994. Minor revisions made January, 1996").
• Quantum Computing and Shor's Algorithm, Matthew Hayward's Quantum Algorithms Page, 2005-02-17, imsa.edu, LaTeX2HTML version of the original LaTeX document, also available as PDF or postscript document.
• Quantum Computation and Shor's Factoring Algorithm, Ronald de Wolf, CWI and University of Amsterdam, January 12, 1999, 9 page postscript document.
• Shor's Factoring Algorithm, Notes from Lecture 9 of Berkeley CS 294–2, dated 4 Oct 2004, 7 page postscript document.
• Chapter 6 Quantum Computation , 91 page postscript document, Caltech, Preskill, PH229.
• Quantum computation: a tutorial by Samuel L. Braunstein.
• The Quantum States of Shor's Algorithm, by Neal Young, Last modified: Tue May 21 11:47:38 1996.
• III. Breaking RSA Encryption with a Quantum Computer: Shor's Factoring Algorithm, Lecture notes on Quantum computation, Cornell University, Physics 481–681, CS 483; Spring, 2006 by N. David Mermin. Last revised 2006-03-28, 30 page PDF document.
• Lavor, C.; Manssur, L. R. U.; Portugal, R. (2003). "Shor's Algorithm for Factoring Large Integers". arXiv:quant-ph/0303175.
• Lomonaco, Jr (2000). "Shor's Quantum Factoring Algorithm". arXiv:quant-ph/0010034. This paper is a written version of a one-hour lecture given on Peter Shor's quantum factoring algorithm. 22 pages.
• Chapter 20 Quantum Computation, from Computational Complexity: A Modern Approach, Draft of a book: Dated January 2007, Sanjeev Arora and Boaz Barak, Princeton University. Published as Chapter 10 Quantum Computation of Sanjeev Arora, Boaz Barak, "Computational Complexity: A Modern Approach", Cambridge University Press, 2009, ISBN 978-0-521-42426-4
• A Step Toward Quantum Computing: Entangling 10 Billion Particles , from "Discover Magazine", Dated January 19, 2011.
• Josef Gruska - Quantum Computing Challenges also in Mathematics unlimited: 2001 and beyond, Editors Björn Engquist, Wilfried Schmid, Springer, 2001, ISBN 978-3-540-66913-5

External links

• Version 1.0.0 of libquantum: contains a C language implementation of Shor's algorithm with their simulated quantum computer library, but the width variable in shor.c should be set to 1 to improve the runtime complexity.
• PBS Infinite Series created two videos explaining the math behind Shor's algorithm, "How to Break Cryptography" and "Hacking at Quantum Speed with Shor's Algorithm".