Degenerate distribution
|
Cumulative distribution function 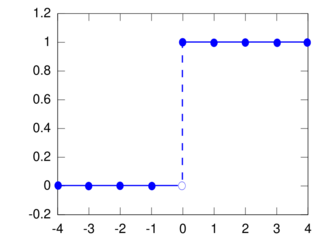 CDF for k0=0. The horizontal axis is x. | |||
| Parameters | |||
|---|---|---|---|
| Support | |||
| pmf | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | undefined | ||
| Kurtosis | undefined | ||
| Entropy | |||
| MGF | |||
| CF | |||
In mathematics, a degenerate distribution is a probability distribution in a space (discrete or continuous) with support only on a space of lower dimension. If the degenerate distribution is univariate (involving only a single random variable) it is a deterministic distribution and takes only a single value. Examples include a two-headed coin and rolling a die whose sides all show the same number. This distribution satisfies the definition of "random variable" even though it does not appear random in the everyday sense of the word; hence it is considered degenerate.
In the case of a real-valued random variable, the degenerate distribution is localized at a point k0 on the real line. The probability mass function equals 1 at this point and 0 elsewhere.
The degenerate univariate distribution can be viewed as the limiting case of a continuous distribution whose variance goes to 0 causing the probability density function to be a delta function at k0, with infinite height there but area equal to 1.
The cumulative distribution function of the univariate degenerate distribution is:
Constant random variable
In probability theory, a constant random variable is a discrete random variable that takes a constant value, regardless of any event that occurs. This is technically different from an almost surely constant random variable, which may take other values, but only on events with probability zero. Constant and almost surely constant random variables, which have a degenerate distribution, provide a way to deal with constant values in a probabilistic framework.
Let X: Ω → R be a random variable defined on a probability space (Ω, P). Then X is an almost surely constant random variable if there exists such that
and is furthermore a constant random variable if
Note that a constant random variable is almost surely constant, but not necessarily vice versa, since if X is almost surely constant then there may exist γ ∈ Ω such that X(γ) ≠ k0 (but then necessarily Pr({γ}) = 0, in fact Pr(X ≠ k0) = 0).
For practical purposes, the distinction between X being constant or almost surely constant is unimportant, since the cumulative distribution function F(x) of X does not depend on whether X is constant or 'merely' almost surely constant. In either case,
The function F(x) is a step function; in particular it is a translation of the Heaviside step function.
Higher dimensions
Degeneracy of a multivariate distribution in n random variables arises when the support lies in a space of dimension less than n. This occurs when at least one of the variables is a deterministic function of the others. For example, in the 2-variable case suppose that Y = aX + b for scalar random variables X and Y and scalar constants a ≠ 0 and b; here knowing the value of one of X or Y gives exact knowledge of the value of the other. All the possible points (x, y) fall on the one-dimensional line y = ax + b.
In general when one or more of n random variables are exactly linearly determined by the others, if the covariance matrix exists its determinant is 0, so it is positive semi-definite but not positive definite, and the joint probability distribution is degenerate.
Degeneracy can also occur even with non-zero covariance. For example, when scalar X is symmetrically distributed about 0 and Y is exactly given by Y = X 2, all possible points (x, y) fall on the parabola y = x 2, which is a one-dimensional subset of the two-dimensional space.
This article does not cite any external source. HandWiki requires at least one external source. See citing external sources. (2021) (Learn how and when to remove this template message) |
 |
