Physics:Baroclinity

Short description: Measure of misalignment between the gradients of pressure and density in a fluid

Density lines and isobars cross vertically in a baroclinic fluid.

Visualization of a (fictive) formation of isotherms (red-orange) and isobars (blue) in a baroclinic atmospheric layering.

File:DIYnamics – Baroclinic eddies in a tank and in Earth's atmosphere.webm In fluid dynamics, the baroclinity (often called baroclinicity) of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure (the fully general case). A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.

Baroclinity is proportional to:

[math]\displaystyle{ \nabla p \times \nabla \rho }[/math]

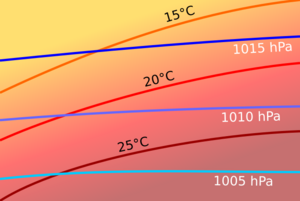
which is proportional to the sine of the angle between surfaces of constant pressure and surfaces of constant density. Thus, in a barotropic fluid (which is defined by zero baroclinity), these surfaces are parallel.

In Earth's atmosphere, barotropic flow is a better approximation in the tropics, where density surfaces and pressure surfaces are both nearly level, whereas in higher latitudes the flow is more baroclinic. These midlatitude belts of high atmospheric baroclinity are characterized by the frequent formation of synoptic-scale cyclones, although these are not really dependent on the baroclinity term per se: for instance, they are commonly studied on pressure coordinate iso-surfaces where that term has no contribution to vorticity production.

Baroclinic instability

Baroclinic instability is a fluid dynamical instability of fundamental importance in the atmosphere and in the oceans. In the atmosphere it is the dominant mechanism shaping the cyclones and anticyclones that dominate weather in mid-latitudes. In the ocean it generates a field of mesoscale eddies (100 km or smaller) that play various roles in oceanic dynamics and the transport of tracers.

Whether a fluid counts as rapidly rotating is determined in this context by the Rossby number, which is a measure of how close the flow is to solid body rotation. More precisely, a flow in solid body rotation has vorticity that is proportional to its angular velocity. The Rossby number is a measure of the departure of the vorticity from that of solid body rotation. The Rossby number must be small for the concept of baroclinic instability to be relevant. When the Rossby number is large, other kinds of instabilities, often referred to as inertial, become more relevant.

The simplest example of a stably stratified flow is an incompressible flow with density decreasing with height.

In a compressible gas such as the atmosphere, the relevant measure is the vertical gradient of the entropy, which must increase with height for the flow to be stably stratified.

The strength of the stratification is measured by asking how large the vertical shear of the horizontal winds has to be in order to destabilize the flow and produce the classic Kelvin–Helmholtz instability. This measure is called the Richardson number. When the Richardson number is large, the stratification is strong enough to prevent this shear instability.

Before the classic work of Jule Charney and Eric Eady on baroclinic instability in the late 1940s, most theories trying to explain the structure of mid-latitude eddies took as their starting points the high Rossby number or small Richardson number instabilities familiar to fluid dynamicists at that time. The most important feature of baroclinic instability is that it exists even in the situation of rapid rotation (small Rossby number) and strong stable stratification (large Richardson's number) typically observed in the atmosphere.

The energy source for baroclinic instability is the potential energy in the environmental flow. As the instability grows, the center of mass of the fluid is lowered. In growing waves in the atmosphere, cold air moving downwards and equatorwards displaces the warmer air moving polewards and upwards.

Baroclinic instability can be investigated in the laboratory using a rotating, fluid filled annulus. The annulus is heated at the outer wall and cooled at the inner wall, and the resulting fluid flows give rise to baroclinically unstable waves.

The term "baroclinic" refers to the mechanism by which vorticity is generated. Vorticity is the curl of the velocity field. In general, the evolution of vorticity can be broken into contributions from advection (as vortex tubes move with the flow), stretching and twisting (as vortex tubes are pulled or twisted by the flow) and baroclinic vorticity generation, which occurs whenever there is a density gradient along surfaces of constant pressure. Baroclinic flows can be contrasted with barotropic flows in which density and pressure surfaces coincide and there is no baroclinic generation of vorticity.

The study of the evolution of these baroclinic instabilities as they grow and then decay is a crucial part of developing theories for the fundamental characteristics of midlatitude weather.

Baroclinic vector

Beginning with the equation of motion for a frictionless fluid (the Euler equations) and taking the curl, one arrives at the equation of motion for the curl of the fluid velocity, that is to say, the vorticity.

In a fluid that is not all of the same density, a source term appears in the vorticity equation whenever surfaces of constant density (isopycnic surfaces) and surfaces of constant pressure (isobaric surfaces) are not aligned. The material derivative of the local vorticity is given by:

[math]\displaystyle{ \frac{D\vec\omega}{Dt} \equiv \frac{\partial\vec{\omega}}{\partial t} + \left(\vec{u} \cdot \vec{\nabla}\right) \vec{\omega} = \left(\vec{\omega} \cdot \vec{\nabla}\right) \vec{u} - \vec{\omega} \left(\vec{\nabla} \cdot \vec{u}\right) + \underbrace{\frac{1}{\rho^2}\vec{\nabla}\rho \times \vec{\nabla}p}_\text{baroclinic contribution} }[/math]

(where [math]\displaystyle{ \vec u }[/math] is the velocity and [math]\displaystyle{ \vec \omega = \vec \nabla \times \vec u }[/math] is the vorticity, [math]\displaystyle{ p }[/math] is the pressure, and [math]\displaystyle{ \rho }[/math] is the density). The baroclinic contribution is the vector:

[math]\displaystyle{ \frac{1}{\rho^2} \vec{\nabla}\rho \times \vec{\nabla}p }[/math]

This vector, sometimes called the solenoidal vector, is of interest both in compressible fluids and in incompressible (but inhomogeneous) fluids. Internal gravity waves as well as unstable Rayleigh–Taylor modes can be analyzed from the perspective of the baroclinic vector. It is also of interest in the creation of vorticity by the passage of shocks through inhomogeneous media, such as in the Richtmyer–Meshkov instability.

Experienced divers are familiar with the very slow waves that can be excited at a thermocline or a halocline, which are known as internal waves. Similar waves can be generated between a layer of water and a layer of oil. When the interface between these two surfaces is not horizontal and the system is close to hydrostatic equilibrium, the gradient of the pressure is vertical but the gradient of the density is not. Therefore the baroclinic vector is nonzero, and the sense of the baroclinic vector is to create vorticity to make the interface level out. In the process, the interface overshoots, and the result is an oscillation which is an internal gravity wave. Unlike surface gravity waves, internal gravity waves do not require a sharp interface. For example, in bodies of water, a gradual gradient in temperature or salinity is sufficient to support internal gravity waves driven by the baroclinic vector.

Bibliography

• Holton, James R. (2004). An Introduction to Dynamic Meteorology. International Geophysics Series. 88 (4th ed.). Burlington, MA: Elsevier Academic Press. ISBN 978-0-12-354015-7. 
• Gill, Adrian E. (1982). Atmosphere-Ocean Dynamics. International Geophysical Series. 30. San Diego, CA: Academic Press. ISBN 978-0-12-283522-3. https://archive.org/details/atmosphereoceand0000gill. 
• Pedlosky, Joseph (1987). Geophysical Fluid Dynamics (2nd ed.). New York: Springer-Verlag. ISBN 978-0-387-96387-7. https://archive.org/details/geophysicalfluid00jose. 
• Tritton, D.J. (1988). Physical Fluid Dynamics (2nd ed.). New York, NJ: Oxford University Press. ISBN 978-0-19-854493-7. 
• Vallis, Geoffrey K. (2007). "Vorticity and Potential Vorticity". Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge: Cambridge University Press. ISBN 978-0-521-84969-2.