Earth:Potential temperature

Short description: Temperature that a fluid would attain if adiabatically brought to a standard reference pressure

The potential temperature of a parcel of fluid at pressure [math]\displaystyle{ P }[/math] is the temperature that the parcel would attain if adiabatically brought to a standard reference pressure [math]\displaystyle{ P_{0} }[/math], usually 1,000 hPa (1,000 mb). The potential temperature is denoted [math]\displaystyle{ \theta }[/math] and, for a gas well-approximated as ideal, is given by

[math]\displaystyle{ \theta = T \left(\frac{P_0}{P}\right)^{R/c_p}, }[/math]

where [math]\displaystyle{ T }[/math] is the current absolute temperature (in K) of the parcel, [math]\displaystyle{ R }[/math] is the gas constant of air, and [math]\displaystyle{ c_p }[/math] is the specific heat capacity at a constant pressure. [math]\displaystyle{ R/c_p = 0.286 }[/math] for air (meteorology). The reference point for potential temperature in the ocean is usually at the ocean's surface which has a water pressure of 0 dbar. The potential temperature in the ocean doesn't account for the varying heat capacities of seawater, therefore it is not a conservative measure of heat content. Graphical representation of potential temperature will always be less than the actual temperature line in a temperature vs depth graph.

Contexts

The concept of potential temperature applies to any stratified fluid. It is most frequently used in the atmospheric sciences and oceanography. The reason that it is used in both fields is that changes in pressure can result in warmer fluid residing under colder fluid – examples being dropping air temperature with altitude and increasing water temperature with depth in very deep ocean trenches and within the ocean mixed layer. When the potential temperature is used instead, these apparently unstable conditions vanish as a parcel of fluid is invariant along its isolines. In the oceans, the potential temperature referenced to the surface will be slightly less than the in-situ temperature (the temperature that a water volume has at the specific depth that the instrument measured it in) since the expansion due to reduction in pressure leads to cooling. The numeric difference between the in situ and potential temperature is almost always less than 1.5 degrees Celsius. However, it's important to use potential temperature when comparing temperatures of water from very different depths.

Comments

Potential temperature is a more dynamically important quantity than the actual temperature. This is because it is not affected by the physical lifting or sinking associated with flow over obstacles or large-scale atmospheric turbulence. A parcel of air moving over a small mountain will expand and cool as it ascends the slope, then compress and warm as it descends on the other side- but the potential temperature will not change in the absence of heating, cooling, evaporation, or condensation (processes that exclude these effects are referred to as dry adiabatic). Since parcels with the same potential temperature can be exchanged without work or heating being required, lines of constant potential temperature are natural flow pathways.

Under almost all circumstances, potential temperature increases upwards in the atmosphere, unlike actual temperature which may increase or decrease. Potential temperature is conserved for all dry adiabatic processes, and as such is an important quantity in the planetary boundary layer (which is often very close to being dry adiabatic).

Potential temperature and hydrostatic stability

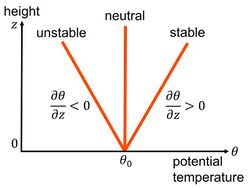
Potential temperature is a useful measure of the static stability of the unsaturated atmosphere. Under normal, stably stratified conditions, the potential temperature increases with height,

[math]\displaystyle{ \frac{\partial \theta}{\partial z} \gt 0 }[/math]

and vertical motions are suppressed. If the potential temperature decreases with height,

[math]\displaystyle{ \frac{\partial \theta}{\partial z} \lt 0 }[/math]

the atmosphere is unstable to vertical motions, and convection is likely. Since convection acts to quickly mix the atmosphere and return to a stably stratified state, observations of decreasing potential temperature with height are uncommon, except while vigorous convection is underway or during periods of strong insolation. Situations in which the equivalent potential temperature decreases with height, indicating instability in saturated air, are much more common.

Since potential temperature is conserved under adiabatic or isentropic air motions, in steady, adiabatic flow lines or surfaces of constant potential temperature act as streamlines or flow surfaces, respectively. This fact is used in isentropic analysis, a form of synoptic analysis which allows visualization of air motions and in particular analysis of large-scale vertical motion.

Potential temperature perturbations

The atmospheric boundary layer (ABL) potential temperature perturbation is defined as the difference between the potential temperature of the ABL and the potential temperature of the free atmosphere above the ABL. This value is called the potential temperature deficit in the case of a katabatic flow, because the surface will always be colder than the free atmosphere and the PT perturbation will be negative.

Derivation

The enthalpy form of the first law of thermodynamics can be written as:

[math]\displaystyle{ dh = T \, ds + v \, dp, }[/math]

where [math]\displaystyle{ dh }[/math] denotes the enthalpy change, [math]\displaystyle{ T }[/math] the temperature, [math]\displaystyle{ ds }[/math] the change in entropy, [math]\displaystyle{ v }[/math] the specific volume, and [math]\displaystyle{ p }[/math] the pressure.

For adiabatic processes, the change in entropy is 0 and the 1st law simplifies to:

[math]\displaystyle{ dh = v \, dp. }[/math]

For approximately ideal gases, such as the dry air in the Earth's atmosphere, the equation of state, [math]\displaystyle{ pv = RT }[/math] can be substituted into the 1st law yielding, after some rearrangement:

[math]\displaystyle{ \frac{dp}{p} = {\frac{c_p}{R}\frac{dT}{T}}, }[/math]

where the [math]\displaystyle{ dh = c_{p}dT }[/math] was used and both terms were divided by the product [math]\displaystyle{ pv }[/math]

Integrating yields:

[math]\displaystyle{ \left(\frac{p_1}{p_0}\right)^{R/c_p} = \frac{T_1}{T_0}, }[/math]

and solving for [math]\displaystyle{ T_{0} }[/math], the temperature a parcel would acquire if moved adiabatically to the pressure level [math]\displaystyle{ p_{0} }[/math], you get:

[math]\displaystyle{ T_0 = T_1 \left(\frac{p_0}{p_1}\right)^{R/c_p} \equiv \theta. }[/math]

Potential virtual temperature

The potential virtual temperature [math]\displaystyle{ \theta_{v} }[/math], defined by

[math]\displaystyle{ \theta_v = \theta \left( 1 + 0.61 r - r_L \right), }[/math]

is the theoretical potential temperature of the dry air which would have the same density as the humid air at a standard pressure P₀. It is used as a practical substitute for density in buoyancy calculations. In this definition [math]\displaystyle{ \theta }[/math] is the potential temperature, [math]\displaystyle{ r }[/math] is the mixing ratio of water vapor, and [math]\displaystyle{ r_L }[/math] is the mixing ratio of liquid water in the air.

Related quantities

The Brunt–Väisälä frequency is a closely related quantity that uses potential temperature and is used extensively in investigations of atmospheric stability.

See also

• Wet-bulb potential temperature
• Atmospheric thermodynamics
• Conservative temperature
• Equivalent potential temperature

Bibliography

• M K Yau and R.R. Rogers, Short Course in Cloud Physics, Third Edition, published by Butterworth-Heinemann, January 1, 1989, 304 pages. ISBN:9780750632157 ISBN:0-7506-3215-1

External links

• Eric Weisstein's World of Physics at Wolfram Research