Erdős–Ko–Rado theorem

Short description: Upper bound on intersecting set families

Two intersecting families of two-element subsets of a four-element set. The sets in the left family all contain the bottom left element. The sets in the right family avoid this element.

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.

The theorem applies to families of sets that all have the same size, [math]\displaystyle{ r }[/math], and are all subsets of some larger set of size [math]\displaystyle{ n }[/math]. One way to construct a family of sets with these parameters, each two sharing an element, is to choose a single element to belong to all the subsets, and then form all of the subsets that contain the chosen element. The Erdős–Ko–Rado theorem states that when [math]\displaystyle{ n }[/math] is large enough for the problem to be nontrivial ([math]\displaystyle{ n\ge 2r }[/math]) this construction produces the largest possible intersecting families. When [math]\displaystyle{ n=2r }[/math] there are other equally-large families, but for larger values of [math]\displaystyle{ n }[/math] only the families constructed in this way can be largest.

The Erdős–Ko–Rado theorem can also be described in terms of hypergraphs or independent sets in Kneser graphs. Several analogous theorems apply to other kinds of mathematical object than sets, including linear subspaces, permutations, and strings. They again describe the largest possible intersecting families as being formed by choosing an element and forming the family of all objects that contain the chosen element.

Statement

Suppose that [math]\displaystyle{ \mathcal{A} }[/math] is a family of distinct [math]\displaystyle{ r }[/math]-element subsets of an [math]\displaystyle{ n }[/math]-element set with [math]\displaystyle{ n\ge 2r }[/math], and that each two subsets share at least one element. Then the theorem states that the number of sets in [math]\displaystyle{ \mathcal{A} }[/math] is at most the binomial coefficient [math]\displaystyle{ \binom{n-1}{r-1}. }[/math] The requirement that [math]\displaystyle{ n\ge 2r }[/math] is necessary for the problem to be nontrivial: when [math]\displaystyle{ n\lt 2r }[/math], all [math]\displaystyle{ r }[/math]-element sets intersect, and the largest intersecting family consists of all [math]\displaystyle{ r }[/math]-element sets, with size [math]\displaystyle{ \tbinom{n}{r} }[/math].

The same result can be formulated as part of the theory of hypergraphs. A family of sets may also be called a hypergraph, and when all the sets (which are called "hyperedges" in this context) are the same size [math]\displaystyle{ r }[/math], it is called an [math]\displaystyle{ r }[/math]-uniform hypergraph. The theorem thus gives an upper bound for the number of pairwise overlapping hyperedges in an [math]\displaystyle{ r }[/math]-uniform hypergraph with [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ n\ge 2r }[/math].

The Kneser graph [math]\displaystyle{ KG_{5,2} }[/math], with a vertex for each 2-element subset of the 5-element set {1,2,3,4,5} and an edge for each pair of disjoint subsets. According to the Erdős–Ko–Rado theorem, the independent sets in this graph have at most four vertices.

The theorem may also be formulated in terms of graph theory: the independence number of the Kneser graph [math]\displaystyle{ KG_{n,r} }[/math] for [math]\displaystyle{ n\ge 2r }[/math] is [math]\displaystyle{ \alpha(KG_{n,r})=\binom{n-1}{r-1}. }[/math] This is a graph with a vertex for each [math]\displaystyle{ r }[/math]-element subset of an [math]\displaystyle{ n }[/math]-element set, and an edge between every pair of disjoint sets. An independent set is a collection of vertices that has no edges between its pairs, and the independence number is the size of the largest independent set. Because Kneser graphs have symmetries taking any vertex to any other vertex (they are vertex-transitive graphs), their fractional chromatic number equals the ratio of their number of vertices to their independence number, so another way of expressing the Erdős–Ko–Rado theorem is that these graphs have fractional chromatic number exactly [math]\displaystyle{ n/r }[/math].

History

Paul Erdős, Chao Ko, and Richard Rado proved this theorem in 1938 after working together on it in England. Rado had moved from Berlin to the University of Cambridge and Erdős from Hungary to the University of Manchester, both escaping the influence of Nazi Germany; Ko was a student of Louis J. Mordell at Manchester. However, they did not publish the result until 1961, with the long delay occurring in part because of a lack of interest in combinatorial set theory in the 1930s, and increased interest in the topic in the 1960s. The 1961 paper stated the result in an apparently more general form, in which the subsets were only required to be size at most [math]\displaystyle{ r }[/math], and to satisfy the additional requirement that no subset be contained in any other. A family of subsets meeting these conditions can be enlarged to subsets of size exactly [math]\displaystyle{ r }[/math] either by an application of Hall's marriage theorem, or by choosing each enlarged subset from the same chain in a symmetric chain decomposition of sets.

Maximum and maximal families

Families of maximum size

The Johnson graph [math]\displaystyle{ J(4,2) }[/math], with a vertex for each two-element subset of {1,2,3,4} and an edge connecting intersecting pairs of subsets, arranged geometrically as an octahedron with disjoint sets at opposite vertices. The largest intersecting families for [math]\displaystyle{ r=2 }[/math] and [math]\displaystyle{ n=2r=4 }[/math] come from the triangular faces of this octahedron. Replacing a set in one of these families by its complement corresponds to moving from a triangle to one of its three neighboring triangles.

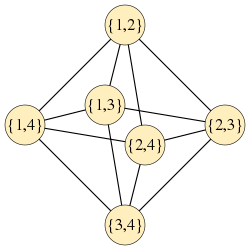
A simple way to construct an intersecting family of [math]\displaystyle{ r }[/math]-element sets whose size exactly matches the Erdős–Ko–Rado bound is to choose any fixed element [math]\displaystyle{ x }[/math], and let [math]\displaystyle{ \mathcal{A} }[/math] consist of all [math]\displaystyle{ r }[/math]-element subsets that include [math]\displaystyle{ x }[/math]. For instance, for 2-element subsets of the 4-element set [math]\displaystyle{ \{1,2,3,4\} }[/math], with [math]\displaystyle{ x=1 }[/math], this produces the family

[math]\displaystyle{ \{1,2\} }[/math], [math]\displaystyle{ \{1,3\} }[/math], and [math]\displaystyle{ \{1,4\} }[/math].

Any two sets in this family intersect, because they both include [math]\displaystyle{ 1 }[/math]. The number of sets is [math]\displaystyle{ \tbinom{n-1}{r-1} }[/math], because after the fixed element is chosen there remain [math]\displaystyle{ n-1 }[/math] other elements to choose, and each set chooses [math]\displaystyle{ r-1 }[/math] of these remaining elements.

When [math]\displaystyle{ n\gt 2r }[/math] this is the only intersecting family of this size. However, when [math]\displaystyle{ n=2r }[/math], there is a more general construction. Each [math]\displaystyle{ r }[/math]-element set can be matched up to its complement, the only [math]\displaystyle{ r }[/math]-element set from which it is disjoint. Then, choose one set from each of these complementary pairs. For instance, for the same parameters above, this more general construction can be used to form the family

[math]\displaystyle{ \{3,4\} }[/math], [math]\displaystyle{ \{2,4\} }[/math], and [math]\displaystyle{ \{2,3\} }[/math],

where every two sets intersect despite no element belonging to all three sets. In this example, all of the sets have been complemented from the ones in the first example, but it is also possible to complement only some of the sets.

When [math]\displaystyle{ n\gt 2r }[/math], families of the first type (variously known as stars, dictatorships, juntas, centered families, or principal families) are the unique maximum families. In this case, a family of nearly-maximum size has an element which is common to almost all of its sets. This property has been called stability, although the same term has also been used for a different property, the fact that (for a wide range of parameters) deleting randomly-chosen edges from the Kneser graph does not increase the size of its independent sets.

Maximal intersecting families

The seven points and seven lines (one drawn as a circle) of the Fano plane form a maximal intersecting family.

An intersecting family of [math]\displaystyle{ r }[/math]-element sets may be maximal, in that no further set can be added (even by extending the ground set) without destroying the intersection property, but not of maximum size. An example with [math]\displaystyle{ n=7 }[/math] and [math]\displaystyle{ r=3 }[/math] is the set of seven lines of the Fano plane, much less than the Erdős–Ko–Rado bound of 15. More generally, the lines of any finite projective plane of order [math]\displaystyle{ q }[/math] form a maximal intersecting family that includes only [math]\displaystyle{ n }[/math] sets, for the parameters [math]\displaystyle{ r=q+1 }[/math] and [math]\displaystyle{ n=q^2+q+1 }[/math]. The Fano plane is the case [math]\displaystyle{ q=2 }[/math] of this construction.

The smallest possible size of a maximal intersecting family of [math]\displaystyle{ r }[/math]-element sets, in terms of [math]\displaystyle{ r }[/math], is unknown but at least [math]\displaystyle{ 3r }[/math] for [math]\displaystyle{ r\ge 4 }[/math]. Projective planes produce maximal intersecting families whose number of sets is [math]\displaystyle{ r^2-r+1 }[/math], but for infinitely many choices of [math]\displaystyle{ r }[/math] there exist smaller maximal intersecting families of size [math]\displaystyle{ \tfrac34r^2 }[/math].

The largest intersecting families of [math]\displaystyle{ r }[/math]-element sets that are maximal but not maximum have size [math]\displaystyle{ \binom{n-1}{r-1}-\binom{n-r-1}{r-1}+1. }[/math] They are formed from an element [math]\displaystyle{ x }[/math] and an [math]\displaystyle{ r }[/math]-element set [math]\displaystyle{ Y }[/math] not containing [math]\displaystyle{ x }[/math], by adding [math]\displaystyle{ Y }[/math] to the family of [math]\displaystyle{ r }[/math]-element sets that include both [math]\displaystyle{ x }[/math] and at least one element of [math]\displaystyle{ Y }[/math]. This result is called the Hilton–Milner theorem, after its proof by Anthony Hilton and Eric Charles Milner in 1967.

Proofs

The original proof of the Erdős–Ko–Rado theorem used induction on [math]\displaystyle{ n }[/math]. The base case, for [math]\displaystyle{ n=2r }[/math], follows easily from the facts that an intersecting family cannot include both a set and its complement, and that in this case the bound of the Erdős–Ko–Rado theorem is exactly half the number of all [math]\displaystyle{ r }[/math]-element sets. The induction step for larger [math]\displaystyle{ n }[/math] uses a method called shifting, of substituting elements in intersecting families to make the family smaller in lexicographic order and reduce it to a canonical form that is easier to analyze.

In 1972, Gyula O. H. Katona gave the following short proof using double counting.

Let [math]\displaystyle{ \mathcal{A} }[/math] be any intersecting family of [math]\displaystyle{ r }[/math]-element subsets of an [math]\displaystyle{ n }[/math]-element set. Arrange all [math]\displaystyle{ n }[/math] elements into any cyclic order, and consider the sets from [math]\displaystyle{ \mathcal{A} }[/math] that form intervals of length [math]\displaystyle{ r }[/math] within this chosen cyclic order. For example if [math]\displaystyle{ n=8 }[/math] and [math]\displaystyle{ r=3 }[/math], one possible cyclic order for the numbers [math]\displaystyle{ \{1,2,...,8\} }[/math] is the order [math]\displaystyle{ (3,1,5,4,2,7,6,8) }[/math], which has eight 3-element intervals (including the ones that wrap around):

[math]\displaystyle{ (3,1,5) }[/math], [math]\displaystyle{ (1,5,4) }[/math], [math]\displaystyle{ (5,4,2) }[/math], [math]\displaystyle{ (4,2,7) }[/math], [math]\displaystyle{ (2,7,6) }[/math], [math]\displaystyle{ (7,6,8) }[/math], [math]\displaystyle{ (6,8,3) }[/math], and [math]\displaystyle{ (8,3,1) }[/math].

However, only some of these intervals can belong to [math]\displaystyle{ \mathcal{A} }[/math], because they do not all intersect. Katona's key observation is that at most [math]\displaystyle{ r }[/math] intervals from a single cyclic order may belong to [math]\displaystyle{ \mathcal{A} }[/math]. This is because, if [math]\displaystyle{ (a_1,a_2,\dots,a_r) }[/math] is one of these intervals, then every other interval of the same cyclic order that belongs to [math]\displaystyle{ \mathcal{A} }[/math] separates [math]\displaystyle{ a_i }[/math] from [math]\displaystyle{ a_{i+1} }[/math], for some [math]\displaystyle{ i }[/math], by containing precisely one of these two elements. The two intervals that separate these elements are disjoint, so at most one of them can belong to [math]\displaystyle{ \mathcal{A} }[/math]. Thus, the number of intervals in [math]\displaystyle{ \mathcal{A} }[/math] is at most one plus the number [math]\displaystyle{ r-1 }[/math] of pairs that can be separated.

Based on this idea, it is possible to count the pairs [math]\displaystyle{ (S,C) }[/math], where [math]\displaystyle{ S }[/math] is a set in [math]\displaystyle{ \mathcal{A} }[/math] and [math]\displaystyle{ C }[/math] is a cyclic order for which [math]\displaystyle{ S }[/math] is an interval, in two ways. First, for each set [math]\displaystyle{ S }[/math] one may generate [math]\displaystyle{ C }[/math] by choosing one of [math]\displaystyle{ r! }[/math] permutations of [math]\displaystyle{ S }[/math] and [math]\displaystyle{ (n-r)! }[/math] permutations of the remaining elements, showing that the number of pairs is [math]\displaystyle{ |\mathcal{A}|r!(n-r)! }[/math]. And second, there are [math]\displaystyle{ (n-1)! }[/math] cyclic orders, each of which has at most [math]\displaystyle{ r }[/math] intervals of [math]\displaystyle{ \mathcal{A} }[/math], so the number of pairs is at most [math]\displaystyle{ r(n-1)! }[/math]. Comparing these two counts gives the inequality [math]\displaystyle{ |\mathcal{A}|r!(n-r)!\le r(n-1)! }[/math] and dividing both sides by [math]\displaystyle{ r!(n-r)! }[/math] gives the result

[math]\displaystyle{ |\mathcal{A}|\le \frac{r(n-1)!}{r!(n-r)!}={n-1\choose r-1}. }[/math]

It is also possible to derive the Erdős–Ko–Rado theorem as a special case of the Kruskal–Katona theorem, another important result in extremal set theory. Many other proofs are known.

Related results

Generalizations

A generalization of the theorem applies to subsets that are required to have large intersections. This version of the theorem has three parameters: [math]\displaystyle{ n }[/math], the number of elements the subsets are drawn from, [math]\displaystyle{ r }[/math], the size of the subsets, as before, and [math]\displaystyle{ t }[/math], the minimum size of the intersection of any two subsets. For the original form of the Erdős–Ko–Rado theorem, [math]\displaystyle{ t=1 }[/math]. In general, for [math]\displaystyle{ n }[/math] large enough with respect to the other two parameters, the generalized theorem states that the size of a [math]\displaystyle{ t }[/math]-intersecting family of subsets is at most [math]\displaystyle{ \binom{n-t}{k-t}. }[/math] More precisely, this bound holds when [math]\displaystyle{ n\ge(t+1)(k-t+1) }[/math], and does not hold for smaller values of [math]\displaystyle{ n }[/math]. When [math]\displaystyle{ n\gt (t+1)(k-t+1) }[/math], the only [math]\displaystyle{ t }[/math]-intersecting families of this size are obtained by designating [math]\displaystyle{ t }[/math] elements as the common intersection of all the subsets, and constructing the family of all [math]\displaystyle{ r }[/math]-element subsets that include these [math]\displaystyle{ t }[/math] designated elements. The maximal size of a t-intersecting family when [math]\displaystyle{ n \lt (t+1)(k-t+1) }[/math] was determined by Ahlswede and Khachatrian, in their Ahlswede–Khachatrian theorem.

The corresponding graph-theoretic formulation of this generalization involves Johnson graphs in place of Kneser graphs. For large enough values of [math]\displaystyle{ n }[/math] and in particular for [math]\displaystyle{ n\gt \tfrac12k^2 }[/math], both the Erdős–Ko–Rado theorem and its generalization can be strengthened from the independence number to the Shannon capacity of a graph: the Johnson graph corresponding to the [math]\displaystyle{ t }[/math]-intersecting [math]\displaystyle{ r }[/math]-element subsets has Shannon capacity [math]\displaystyle{ \tbinom{n-t}{k-t} }[/math].

The theorem can also be generalized to families in which every [math]\displaystyle{ h }[/math] subsets have a common intersection. Because this strengthens the condition that every pair intersects (for which [math]\displaystyle{ h=2 }[/math]), these families have the same bound on their maximum size, [math]\displaystyle{ \tbinom{n-1}{r-1} }[/math] when [math]\displaystyle{ n }[/math] is sufficiently large. However, in this case the meaning of "sufficiently large" can be relaxed from [math]\displaystyle{ n\ge 2r }[/math] to [math]\displaystyle{ n\ge \tfrac{h}{h-1}r }[/math].

Analogs

Many results analogous to the Erdős–Ko–Rado theorem, but for other classes of objects than finite sets, are known. These generally involve a statement that the largest families of intersecting objects, for some definition of intersection, are obtained by choosing an element and constructing the family of all objects that include that chosen element. Examples include the following:

There is a q-analog of the Erdős–Ko–Rado theorem for intersecting families of linear subspaces over finite fields. If [math]\displaystyle{ \mathcal{S} }[/math] is an intersecting family of [math]\displaystyle{ k }[/math]-dimensional subspaces of an [math]\displaystyle{ n }[/math]-dimensional vector space over a finite field of order [math]\displaystyle{ q }[/math], and [math]\displaystyle{ n \ge 2k }[/math], then [math]\displaystyle{ |\mathcal{S}| \le \binom{n-1}{k-1}_q, }[/math] where the subscript q marks the notation for the Gaussian binomial coefficient, the number of subspaces of a given dimension within a vector space of a larger dimension over a finite field of order q. In this case, a largest intersecting family of subspaces may be obtained by choosing any nonzero vector and constructing the family of subspaces of the given dimension that all contain the chosen vector.

Two permutations on the same set of elements are defined to be intersecting if there is some element that has the same image under both permutations. On an [math]\displaystyle{ n }[/math]-element set, there is an obvious family of [math]\displaystyle{ (n-1)! }[/math] intersecting permutations, the permutations that fix one of the elements (the stabilizer subgroup of this element). The analogous theorem is that no intersecting family of permutations can be larger, and that the only intersecting families of size [math]\displaystyle{ (n-1)! }[/math] are the cosets of one-element stabilizers. These can be described more directly as the families of permutations that map some fixed element to another fixed element. More generally, for any [math]\displaystyle{ t }[/math] and sufficiently large [math]\displaystyle{ n }[/math], a family of permutations each pair of which has [math]\displaystyle{ t }[/math] elements in common has maximum size [math]\displaystyle{ (n-t)! }[/math], and the only families of this size are cosets of pointwise stabilizers. Alternatively, in graph theoretic terms, the [math]\displaystyle{ n }[/math]-element permutations correspond to the perfect matchings of a complete bipartite graph [math]\displaystyle{ K_{n,n} }[/math] and the theorem states that, among families of perfect matchings each pair of which share [math]\displaystyle{ t }[/math] edges, the largest families are formed by the matchings that all contain [math]\displaystyle{ t }[/math] chosen edges. Another analog of the theorem, for partitions of a set, includes as a special case the perfect matchings of a complete graph [math]\displaystyle{ K_n }[/math] (with [math]\displaystyle{ n }[/math] even). There are [math]\displaystyle{ (n-1)!! }[/math] matchings, where [math]\displaystyle{ !! }[/math] denotes the double factorial. The largest family of matchings that pairwise intersect (meaning that they have an edge in common) has size [math]\displaystyle{ (n-3)!! }[/math] and is obtained by fixing one edge and choosing all ways of matching the remaining [math]\displaystyle{ n-2 }[/math] vertices.

A partial geometry is a system of finitely many abstract points and lines, satisfying certain axioms including the requirement that all lines contain the same number of points and all points belong to the same number of lines. In a partial geometry, a largest system of pairwise-intersecting lines can be obtained from the set of lines through any single point.

A signed set consists of a set together with sign function that maps each element to [math]\displaystyle{ \{1,-1\} }[/math]. Two signed sets may be said to intersect when they have a common element that has the same sign in each of them. Then an intersecting family of [math]\displaystyle{ r }[/math]-element signed sets, drawn from an [math]\displaystyle{ n }[/math]-element universe, consists of at most [math]\displaystyle{ 2^{r-1}\binom{n-1}{r-1} }[/math] signed sets. This number of signed sets may be obtained by fixing one element and its sign and letting the remaining [math]\displaystyle{ r-1 }[/math] elements and signs vary.

For strings of length [math]\displaystyle{ n }[/math] over an alphabet of size [math]\displaystyle{ q }[/math], two strings can be defined to intersect if they have a position where both share the same symbol. The largest intersecting families are obtained by choosing one position and a fixed symbol for that position, and letting the rest of the positions vary arbitrarily. These families consist of [math]\displaystyle{ q^{n-1} }[/math] strings, and are the only pairwise intersecting families of this size. More generally, the largest families of strings in which every two have [math]\displaystyle{ t }[/math] positions with equal symbols are obtained by choosing [math]\displaystyle{ t+2i }[/math] positions and symbols for those positions, for a number [math]\displaystyle{ i }[/math] that depends on [math]\displaystyle{ n }[/math], [math]\displaystyle{ q }[/math], and [math]\displaystyle{ t }[/math], and constructing the family of strings that each have at least [math]\displaystyle{ t+i }[/math] of the chosen symbols. These results can be interpreted graph-theoretically in terms of the Hamming scheme.

Unsolved problem in mathematics: Is the largest family of intersecting triangulations of a convex polygon obtained by cutting off one vertex and choosing all triangulations of the remaining polygon? (more unsolved problems in mathematics)

An unproven conjecture, posed by Gil Kalai and Karen Meagher, concerns another analog for the family of triangulations of a convex polygon with [math]\displaystyle{ n }[/math] vertices. The number of all triangulations is a Catalan number [math]\displaystyle{ C_{n-2} }[/math], and the conjecture states that a family of triangulations every pair of which shares an edge has maximum size [math]\displaystyle{ C_{n-3} }[/math]. An intersecting family of size exactly [math]\displaystyle{ C_{n-3} }[/math] may be obtained by cutting off a single vertex of the polygon by a triangle, and choosing all ways of triangulating the remaining [math]\displaystyle{ (n-1) }[/math]-vertex polygon.

Applications

The Erdős–Ko–Rado theorem can be used to prove the following result in probability theory. Let [math]\displaystyle{ x_i }[/math] be independent 0–1 random variables with probability [math]\displaystyle{ p\ge\tfrac12 }[/math] of being one, and let [math]\displaystyle{ c(\vec x) }[/math] be any fixed convex combination of these variables. Then [math]\displaystyle{ \Pr\left[c(\vec x)\ge\tfrac12\right]\ge p. }[/math] The proof involves observing that subsets of variables whose indicator vectors have large convex combinations must be non-disjoint and using the Erdős–Ko–Rado theorem to bound the number of these subsets.

The stability properties of the Erdős–Ko–Rado theorem play a key role in an efficient algorithm for finding monochromatic edges in improper colorings of Kneser graphs. The Erdős–Ko–Rado theorem has also been used to characterize the symmetries of the space of phylogenetic trees.

See also

• Helly's theorem, on conditions ensuring that intersecting families of convex sets have a common intersection
• Sperner's theorem, an upper bound on families of pairwise non-nested sets
• Steiner system, maximum-sized uniform set families in which no pair (rather than every pair) has a large intersection
• Sunflower (mathematics), a family of sets where (unlike the maximum intersecting families here) all pairs have equal intersections
• Thrackle, an unsolved problem on the size of families of intersecting curves

References

Works cited

• Ahlswede, Rudolf; Khachatrian, Levon H. (1997). "The complete intersection theorem for systems of finite sets". European Journal of Combinatorics 18: 125–136. doi:10.1006/eujc.1995.0092. 
• Ahlswede, Rudolf; Khachatrian, Levon H. (1998), "The diametric theorem in Hamming spaces—optimal anticodes", Advances in Applied Mathematics 20 (4): 429–449, doi:10.1006/aama.1998.0588 
• "Chapter 30: Three famous theorems on finite sets", Proofs from THE BOOK (6th ed.), Springer, 2018, pp. 213–217, doi:10.1007/978-3-662-57265-8_15, ISBN 978-3-662-57265-8 
• Anderson, Ian (1987), "Chapter 5: Intersecting systems and the Erdős–Ko–Rado theorem", Combinatorics of Finite Sets, Oxford Science Publications, Oxford University Press, pp. 70–86, ISBN 0-19-853367-5 
• Anderson, Ian (2013), "Combinatorial set theory", Combinatorics: Ancient and Modern, Oxford University Press, pp. 309–328, doi:10.1093/acprof:oso/9780199656592.003.0014, ISBN 978-0-19-965659-2 
• "Sharp threshold for the Erdős–Ko–Rado theorem", Random Structures & Algorithms 62: 3–28, 2022, doi:10.1002/rsa.21090 
• "An Erdős–Ko–Rado theorem for signed sets", Computers and Mathematics with Applications 34 (11): 9–13, 1997, doi:10.1016/S0898-1221(97)00215-0 
• "On the stability of the Erdős-Ko-Rado theorem", Journal of Combinatorial Theory, Series A 137: 64–78, 2016, doi:10.1016/j.jcta.2015.08.002 
• Borg, Peter (2012), "Cross-intersecting sub-families of hereditary families", Journal of Combinatorial Theory, Series A 119 (4): 871–881, doi:10.1016/j.jcta.2011.12.002 
• "Intersecting families of permutations", European Journal of Combinatorics 24 (7): 881–890, 2003, doi:10.1016/S0195-6698(03)00078-7 
• Das, Shagnik; Tran, Tuan (2016), "Removal and stability for Erdős–Ko–Rado", SIAM Journal on Discrete Mathematics 30 (2): 1102–1114, doi:10.1137/15M105149X 
• "Erdős–Ko–Rado theorem – 22 years later", SIAM Journal on Algebraic and Discrete Methods 4 (4): 419–431, 1983, doi:10.1137/0604042 
• "Intersecting families are essentially contained in juntas", Combinatorics, Probability and Computing 18 (1–2): 107–122, 2009, doi:10.1017/S0963548308009309 
• Dow, Stephen J.; Drake, David A. (1985), "A lower bound for the cardinality of a maximal family of mutually intersecting sets of equal size", Congressus Numerantium 48: 47–48 
• Ellis, David; Friedgut, Ehud; Pilpel, Haran (2011), "Intersecting families of permutations", Journal of the American Mathematical Society 24 (3): 649–682, doi:10.1090/S0894-0347-2011-00690-5 
• Whitehead, C., ed. (1987), "My joint work with Richard Rado", Surveys in combinatorics, 1987: Invited Papers for the Eleventh British Combinatorial Conference, London Mathematical Society Lecture Note Series, 123, Cambridge University Press, pp. 53–80, ISBN 978-0-521-34805-8, https://www.renyi.hu/~p_erdos/1987-12.pdf 
• "Intersection theorems for systems of finite sets", Quarterly Journal of Mathematics, Second Series 12: 313–320, 1961, doi:10.1093/qmath/12.1.313, https://www.renyi.hu/~p_erdos/1961-07.pdf 
• "On Sperner families satisfying an additional condition", Journal of Combinatorial Theory, Series A 20 (1): 1–11, 1976, doi:10.1016/0097-3165(76)90073-x 
• "On the maximum number of permutations with given maximal or minimal distance", Journal of Combinatorial Theory, Series A 22 (3): 352–360, 1977, doi:10.1016/0097-3165(77)90009-7 
• "Nontrivial intersecting families", Journal of Combinatorial Theory, Series A 41 (1): 150–153, 1986, doi:10.1016/0097-3165(86)90121-4 
• "Old and new proofs of the Erdős–Ko–Rado theorem", Journal of Sichuan University Natural Science Edition 26 (Special Issue): 112–122, 1989, https://mathweb.ucsd.edu/~fan/ron/papers/90_03_erdos_ko_rado.pdf 
• "The Erdős–Ko–Rado theorem for vector spaces", Journal of Combinatorial Theory, Series A 43 (2): 228–236, 1986, doi:10.1016/0097-3165(86)90063-4 
• Friedgut, Ehud (2008), "On the measure of intersecting families, uniqueness and stability", Combinatorica 28 (5): 503–528, doi:10.1007/s00493-008-2318-9, https://www.ma.huji.ac.il/~ehudf/docs/X%5E2=0.pdf 
• "On maximal intersecting families of finite sets", Journal of Combinatorial Theory, Series A 28 (3): 282–289, 1980, doi:10.1016/0097-3165(80)90071-0 
• "Extremal hypergraphs and combinatorial geometry", Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Zürich, 1994), Basel: Birkhäuser, 1995, pp. 1343–1352, doi:10.1007/978-3-0348-9078-6_65, https://web.archive.org/web/20170830012752id_/http://www.mathunion.org/ICM/ICM1994.2/Main/icm1994.2.1343.1352.ocr.pdf 
• "A new proof of the Erdős–Ko–Rado theorem for intersecting families of permutations", European Journal of Combinatorics 30 (2): 404–414, 2009, doi:10.1016/j.ejc.2008.05.006 
• Erdős–Ko–Rado Theorems: Algebraic Approaches, Cambridge Studies in Advanced Mathematics, Cambridge University Press, 2015, ISBN 9781107128446, https://www.cambridge.org/ht/academic/subjects/mathematics/discrete-mathematics-information-theory-and-coding/erdoskorado-theorems-algebraic-approaches 
• Grindstaff, Gillian (2020), "The isometry group of phylogenetic tree space is S_n", Proceedings of the American Mathematical Society 148 (10): 4225–4233, doi:10.1090/proc/15154 
• Harvey, Daniel J. (2014), "Treewidth of the Kneser graph and the Erdős–Ko–Rado theorem", Electronic Journal of Combinatorics 21 (1): Paper 1.48, doi:10.37236/3971 
• Haviv, Ishay (2022), "A fixed-parameter algorithm for the Kneser problem", in Bojanczyk, Mikolaj; Merelli, Emanuela; Woodruff, David P., 49th International Colloquium on Automata, Languages, and Programming, ICALP 2022, July 4–8, 2022, Paris, France, LIPIcs, 229, Schloss Dagstuhl – Leibniz-Zentrum für Informatik, pp. 72:1–72:18, doi:10.4230/LIPIcs.ICALP.2022.72, ISBN 9783959772358 
• "Some intersection theorems for systems of finite sets", Quarterly Journal of Mathematics, Second Series 18: 369–384, 1967, doi:10.1093/qmath/18.1.369 
• "A simple proof of the Erdös–Chao Ko–Rado theorem", Journal of Combinatorial Theory, Series B 13 (2): 183–184, 1972, doi:10.1016/0095-8956(72)90054-8 
• Larose, Benoit (2004), "Stable sets of maximal size in Kneser-type graphs", European Journal of Combinatorics 25 (5): 657–673, doi:10.1016/j.ejc.2003.10.006 
• Liggett, Thomas M. (1977), "Extensions of the Erdős–Ko–Rado theorem and a statistical application", Journal of Combinatorial Theory, Series A 23 (1): 15–21, doi:10.1016/0097-3165(77)90075-9 
• A Course in Combinatorics, Cambridge University Press, Cambridge, 1992, pp. 45–46, ISBN 0-521-41057-6 
• Olarte, Jorge Alberto (2020), "The EKR property for flag pure simplicial complexes without boundary", Journal of Combinatorial Theory, Series A 172: 105205, 29, doi:10.1016/j.jcta.2019.105205, https://www.maths.usyd.edu.au/u/pubs/publist/preprints/2019/olarte-18.pdf 
• Polcyn, Joanna; Ruciński, Andrzej (2017), "A hierarchy of maximal intersecting triple systems", Opuscula Mathematica 37 (4): 597–608, doi:10.7494/OpMath.2017.37.4.597 
• "Association schemes and the Shannon capacity: Eberlein polynomials and the Erdős–Ko–Rado theorem", Algebraic Methods in Graph Theory, Vol. I, II: Papers from the Conference held in Szeged, August 24–31, 1978, Colloquia Mathematica Societatis János Bolyai, 25, North-Holland, 1981, pp. 671–688 
• "The exact bound in the Erdős–Ko–Rado theorem", Combinatorica 4 (2–3): 247–257, 1984, doi:10.1007/BF02579226 

External links

• Cameron, Peter (September 29, 2017), "EKR, Steiner systems, association schemes, and all that", Peter Cameron's Blog, https://cameroncounts.wordpress.com/2017/09/29/ekr-steiner-systems-association-schemes-and-all-that/