Gated recurrent unit
| Machine learning and data mining |
|---|
 |
Gated recurrent units (GRUs) are a gating mechanism in recurrent neural networks, introduced in 2014 by Kyunghyun Cho et al.[1] The GRU is like a long short-term memory (LSTM) with a gating mechanism to input or forget certain features,[2] but lacks a context vector or output gate, resulting in fewer parameters than LSTM.[3] GRU's performance on certain tasks of polyphonic music modeling, speech signal modeling and natural language processing was found to be similar to that of LSTM.[4][5] GRUs showed that gating is indeed helpful in general, and Bengio's team came to no concrete conclusion on which of the two gating units was better.[6][7]
Architecture
There are several variations on the full gated unit, with gating done using the previous hidden state and the bias in various combinations, and a simplified form called minimal gated unit.[8]
The operator [math]\displaystyle{ \odot }[/math] denotes the Hadamard product in the following.
Fully gated unit
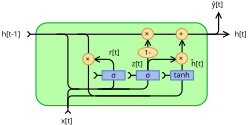
Initially, for [math]\displaystyle{ t = 0 }[/math], the output vector is [math]\displaystyle{ h_0 = 0 }[/math].
- [math]\displaystyle{ \begin{align} z_t &= \sigma(W_{z} x_t + U_{z} h_{t-1} + b_z) \\ r_t &= \sigma(W_{r} x_t + U_{r} h_{t-1} + b_r) \\ \hat{h}_t &= \phi(W_{h} x_t + U_{h} (r_t \odot h_{t-1}) + b_h) \\ h_t &= (1-z_t) \odot h_{t-1} + z_t \odot \hat{h}_t \end{align} }[/math]
Variables ([math]\displaystyle{ d }[/math] denotes the number of input features and [math]\displaystyle{ e }[/math] the number of output features):
- [math]\displaystyle{ x_t \in \mathbb{R}^{d} }[/math]: input vector
- [math]\displaystyle{ h_t \in \mathbb{R}^{e} }[/math]: output vector
- [math]\displaystyle{ \hat{h}_t \in \mathbb{R}^{e} }[/math]: candidate activation vector
- [math]\displaystyle{ z_t \in (0,1)^{e} }[/math]: update gate vector
- [math]\displaystyle{ r_t \in (0,1)^{e} }[/math]: reset gate vector
- [math]\displaystyle{ W \in \mathbb{R}^{d \times e} }[/math], [math]\displaystyle{ U \in \mathbb{R}^{e \times e} }[/math] and [math]\displaystyle{ b \in \mathbb{R}^{e} }[/math]: parameter matrices and vector which need to be learned during training
- [math]\displaystyle{ \sigma }[/math]: The original is a logistic function.
- [math]\displaystyle{ \phi }[/math]: The original is a hyperbolic tangent.
Alternative activation functions are possible, provided that [math]\displaystyle{ \sigma(x) \isin [0, 1] }[/math].
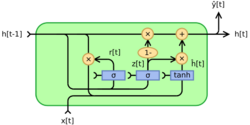
Alternate forms can be created by changing [math]\displaystyle{ z_t }[/math] and [math]\displaystyle{ r_t }[/math][9]
- Type 1, each gate depends only on the previous hidden state and the bias.
- [math]\displaystyle{ \begin{align} z_t &= \sigma(U_{z} h_{t-1} + b_z) \\ r_t &= \sigma(U_{r} h_{t-1} + b_r) \\ \end{align} }[/math]
- Type 2, each gate depends only on the previous hidden state.
- [math]\displaystyle{ \begin{align} z_t &= \sigma(U_{z} h_{t-1}) \\ r_t &= \sigma(U_{r} h_{t-1}) \\ \end{align} }[/math]
- Type 3, each gate is computed using only the bias.
- [math]\displaystyle{ \begin{align} z_t &= \sigma(b_z) \\ r_t &= \sigma(b_r) \\ \end{align} }[/math]
Minimal gated unit
The minimal gated unit (MGU) is similar to the fully gated unit, except the update and reset gate vector is merged into a forget gate. This also implies that the equation for the output vector must be changed:[10]
- [math]\displaystyle{ \begin{align} f_t &= \sigma(W_{f} x_t + U_{f} h_{t-1} + b_f) \\ \hat{h}_t &= \phi(W_{h} x_t + U_{h} (f_t \odot h_{t-1}) + b_h) \\ h_t &= (1-f_t) \odot h_{t-1} + f_t \odot \hat{h}_t \end{align} }[/math]
Variables
- [math]\displaystyle{ x_t }[/math]: input vector
- [math]\displaystyle{ h_t }[/math]: output vector
- [math]\displaystyle{ \hat{h}_t }[/math]: candidate activation vector
- [math]\displaystyle{ f_t }[/math]: forget vector
- [math]\displaystyle{ W }[/math], [math]\displaystyle{ U }[/math] and [math]\displaystyle{ b }[/math]: parameter matrices and vector
Light gated recurrent unit
The light gated recurrent unit (LiGRU)[4] removes the reset gate altogether, replaces tanh with the ReLU activation, and applies batch normalization (BN):
- [math]\displaystyle{ \begin{align} z_t &= \sigma(\operatorname{BN}(W_z x_t) + U_z h_{t-1}) \\ \tilde{h}_t &= \operatorname{ReLU}(\operatorname{BN}(W_h x_t) + U_h h_{t-1}) \\ h_t &= z_t \odot h_{t-1} + (1 - z_t) \odot \tilde{h}_t \end{align} }[/math]
LiGRU has been studied from a Bayesian perspective.[11] This analysis yielded a variant called light Bayesian recurrent unit (LiBRU), which showed slight improvements over the LiGRU on speech recognition tasks.
References
- ↑ Cho, Kyunghyun; van Merrienboer, Bart; Bahdanau, DZmitry; Bougares, Fethi; Schwenk, Holger; Bengio, Yoshua (2014). "Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation". Association for Computational Linguistics.
- ↑ Felix Gers; Jürgen Schmidhuber; Fred Cummins (1999). "Learning to forget: Continual prediction with LSTM". 9th International Conference on Artificial Neural Networks: ICANN '99. 1999. pp. 850–855. doi:10.1049/cp:19991218. ISBN 0-85296-721-7. https://ieeexplore.ieee.org/document/818041.
- ↑ "Recurrent Neural Network Tutorial, Part 4 – Implementing a GRU/LSTM RNN with Python and Theano – WildML". 2015-10-27. http://www.wildml.com/2015/10/recurrent-neural-network-tutorial-part-4-implementing-a-grulstm-rnn-with-python-and-theano/.
- ↑ 4.0 4.1 Ravanelli, Mirco; Brakel, Philemon; Omologo, Maurizio; Bengio, Yoshua (2018). "Light Gated Recurrent Units for Speech Recognition". IEEE Transactions on Emerging Topics in Computational Intelligence 2 (2): 92–102. doi:10.1109/TETCI.2017.2762739.
- ↑ Su, Yuahang; Kuo, Jay (2019). "On extended long short-term memory and dependent bidirectional recurrent neural network". Neurocomputing 356: 151–161. doi:10.1016/j.neucom.2019.04.044.
- ↑ Chung, Junyoung; Gulcehre, Caglar; Cho, KyungHyun; Bengio, Yoshua (2014). "Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling". arXiv:1412.3555 [cs.NE].
- ↑ Gruber, N.; Jockisch, A. (2020), "Are GRU cells more specific and LSTM cells more sensitive in motive classification of text?", Frontiers in Artificial Intelligence 3: 40, doi:10.3389/frai.2020.00040, PMID 33733157
- ↑ Chung, Junyoung; Gulcehre, Caglar; Cho, KyungHyun; Bengio, Yoshua (2014). "Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling". arXiv:1412.3555 [cs.NE].
- ↑ Dey, Rahul; Salem, Fathi M. (2017-01-20). "Gate-Variants of Gated Recurrent Unit (GRU) Neural Networks". arXiv:1701.05923 [cs.NE].
- ↑ Heck, Joel; Salem, Fathi M. (2017-01-12). "Simplified Minimal Gated Unit Variations for Recurrent Neural Networks". arXiv:1701.03452 [cs.NE].
- ↑ Bittar, Alexandre; Garner, Philip N. (May 2021). "A Bayesian Interpretation of the Light Gated Recurrent Unit". 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Toronto, ON, Canada: IEEE. pp. 2965–2969. 10.1109/ICASSP39728.2021.9414259. https://ieeexplore.ieee.org/document/9414259.
 |  |
