HMAC

Short description: Computer communications hash algorithm

HMAC-SHA1 generation

In cryptography, an HMAC (sometimes expanded as either keyed-hash message authentication code or hash-based message authentication code) is a specific type of message authentication code (MAC) involving a cryptographic hash function and a secret cryptographic key. As with any MAC, it may be used to simultaneously verify both the data integrity and authenticity of a message. An HMAC is a type of keyed hash function that can also be used in a key derivation scheme or a key stretching scheme.

HMAC can provide authentication using a shared secret instead of using digital signatures with asymmetric cryptography. It trades off the need for a complex public key infrastructure by delegating the key exchange to the communicating parties, who are responsible for establishing and using a trusted channel to agree on the key prior to communication.

Details

Any cryptographic hash function, such as SHA-2 or SHA-3, may be used in the calculation of an HMAC; the resulting MAC algorithm is termed HMAC-X, where X is the hash function used (e.g. HMAC-SHA256 or HMAC-SHA3-512). The cryptographic strength of the HMAC depends upon the cryptographic strength of the underlying hash function, the size of its hash output, and the size and quality of the key.

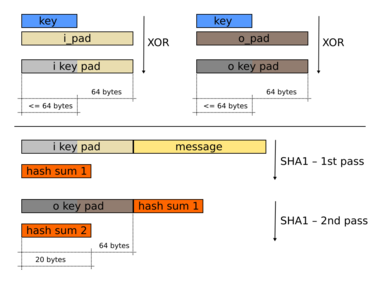
HMAC uses two passes of hash computation. Before either pass, the secret key is used to derive two keys – inner and outer. Next, the first pass of the hash algorithm produces an internal hash derived from the message and the inner key. The second pass produces the final HMAC code derived from the inner hash result and the outer key. Thus the algorithm provides better immunity against length extension attacks.

An iterative hash function (one that uses the Merkle–Damgård construction) breaks up a message into blocks of a fixed size and iterates over them with a compression function. For example, SHA-256 operates on 512-bit blocks. The size of the output of HMAC is the same as that of the underlying hash function (e.g., 256 and 512 bits in the case of SHA-256 and SHA3-512, respectively), although it can be truncated if desired.

HMAC does not encrypt the message. Instead, the message (encrypted or not) must be sent alongside the HMAC hash. Parties with the secret key will hash the message again themselves, and if it is authentic, the received and computed hashes will match.

The definition and analysis of the HMAC construction was first published in 1996 in a paper by Mihir Bellare, Ran Canetti, and Hugo Krawczyk, and they also wrote RFC 2104 in 1997. The 1996 paper also defined a nested variant called NMAC (Nested MAC). FIPS PUB 198 generalizes and standardizes the use of HMACs. HMAC is used within the IPsec, SSH and TLS protocols and for JSON Web Tokens.

Definition

This definition is taken from RFC 2104:

[math]\displaystyle{ \begin{align} \operatorname{HMAC}(K, m) &= \operatorname{H}\Bigl(\bigl(K' \oplus opad\bigr) \parallel \operatorname{H} \bigl(\left(K' \oplus ipad\right) \parallel m\bigr)\Bigr) \\ K' &= \begin{cases} \operatorname{H}\left(K\right) & \text{if}\ K\text{ is larger than block size} \\ K & \text{otherwise} \end{cases} \end{align} }[/math]

where

[math]\displaystyle{ \operatorname{H} }[/math] is a cryptographic hash function.

[math]\displaystyle{ m }[/math] is the message to be authenticated.

[math]\displaystyle{ K }[/math] is the secret key.

[math]\displaystyle{ K' }[/math] is a block-sized key derived from the secret key, K; either by padding to the right with 0s up to the block size, or by hashing down to less than or equal to the block size first and then padding to the right with zeros.

[math]\displaystyle{ \parallel }[/math] denotes concatenation.

[math]\displaystyle{ \oplus }[/math] denotes bitwise exclusive or (XOR).

[math]\displaystyle{ opad }[/math] is the block-sized outer padding, consisting of repeated bytes valued 0x5c.

[math]\displaystyle{ ipad }[/math] is the block-sized inner padding, consisting of repeated bytes valued 0x36.

Hash function H	b, bytes	L, bytes
MD5	64	16
SHA-1	64	20
SHA-224	64	28
SHA-256	64	32
SHA-512/224	128	28
SHA-512/256	128	32
SHA-384	128	48
SHA-512	128	64
SHA3-224	144	28
SHA3-256	136	32
SHA3-384	104	48
SHA3-512	72	64
out = H( in ) L = length( out ) b = H's internal block length

Implementation

The following pseudocode demonstrates how HMAC may be implemented. The block size is 512 bits (64 bytes) when using one of the following hash functions: SHA-1, MD5, RIPEMD-128.

function hmac is
    input:
        key:        Bytes    // Array of bytes
        message:    Bytes    // Array of bytes to be hashed
        hash:       Function // The hash function to use (e.g. SHA-1)
        blockSize:  Integer  // The block size of the hash function (e.g. 64 bytes for SHA-1)
        outputSize: Integer  // The output size of the hash function (e.g. 20 bytes for SHA-1)

    // Compute the block sized key
    block_sized_key = computeBlockSizedKey(key, hash, blockSize)

    o_key_pad ← block_sized_key xor [0x5c blockSize]   // Outer padded key
    i_key_pad ← block_sized_key xor [0x36 blockSize]   // Inner padded key

    return  hash(o_key_pad ∥ hash(i_key_pad ∥ message))

function computeBlockSizedKey is
    input:
        key:        Bytes    // Array of bytes
        hash:       Function // The hash function to use (e.g. SHA-1)
        blockSize:  Integer  // The block size of the hash function (e.g. 64 bytes for SHA-1)
 
    // Keys longer than blockSize are shortened by hashing them
    if (length(key) > blockSize) then
        key = hash(key)

    // Keys shorter than blockSize are padded to blockSize by padding with zeros on the right
    if (length(key) < blockSize) then
        return  Pad(key, blockSize) // Pad key with zeros to make it blockSize bytes long

    return  key

Design principles

The design of the HMAC specification was motivated by the existence of attacks on more trivial mechanisms for combining a key with a hash function. For example, one might assume the same security that HMAC provides could be achieved with MAC = H(key ∥ message). However, this method suffers from a serious flaw: with most hash functions, it is easy to append data to the message without knowing the key and obtain another valid MAC ("length-extension attack"). The alternative, appending the key using MAC = H(message ∥ key), suffers from the problem that an attacker who can find a collision in the (unkeyed) hash function has a collision in the MAC (as two messages m1 and m2 yielding the same hash will provide the same start condition to the hash function before the appended key is hashed, hence the final hash will be the same). Using MAC = H(key ∥ message ∥ key) is better, but various security papers have suggested vulnerabilities with this approach, even when two different keys are used.

No known extension attacks have been found against the current HMAC specification which is defined as H(key ∥ H(key ∥ message)) because the outer application of the hash function masks the intermediate result of the internal hash. The values of ipad and opad are not critical to the security of the algorithm, but were defined in such a way to have a large Hamming distance from each other and so the inner and outer keys will have fewer bits in common. The security reduction of HMAC does require them to be different in at least one bit.

The Keccak hash function, that was selected by NIST as the SHA-3 competition winner, doesn't need this nested approach and can be used to generate a MAC by simply prepending the key to the message, as it is not susceptible to length-extension attacks.

Security

The cryptographic strength of the HMAC depends upon the size of the secret key that is used and the security of the underlying hash function used. It has been proven that the security of an HMAC construction is directly related to security properties of the hash function used. The most common attack against HMACs is brute force to uncover the secret key. HMACs are substantially less affected by collisions than their underlying hashing algorithms alone. In particular, Mihir Bellare proved that HMAC is a pseudo-random function (PRF) under the sole assumption that the compression function is a PRF. Therefore, HMAC-MD5 does not suffer from the same weaknesses that have been found in MD5.

RFC 2104 requires that "keys longer than B bytes are first hashed using H" which leads to a confusing pseudo-collision: if the key is longer than the hash block size (e.g. 64 bytes for SHA-1), then HMAC(k, m) is computed as HMAC(H(k), m).This property is sometimes raised as a possible weakness of HMAC in password-hashing scenarios: it has been demonstrated that it's possible to find a long ASCII string and a random value whose hash will be also an ASCII string, and both values will produce the same HMAC output.

In 2006, Jongsung Kim, Alex Biryukov, Bart Preneel, and Seokhie Hong showed how to distinguish HMAC with reduced versions of MD5 and SHA-1 or full versions of HAVAL, MD4, and SHA-0 from a random function or HMAC with a random function. Differential distinguishers allow an attacker to devise a forgery attack on HMAC. Furthermore, differential and rectangle distinguishers can lead to second-preimage attacks. HMAC with the full version of MD4 can be forged with this knowledge. These attacks do not contradict the security proof of HMAC, but provide insight into HMAC based on existing cryptographic hash functions.

In 2009, Xiaoyun Wang et al. presented a distinguishing attack on HMAC-MD5 without using related keys. It can distinguish an instantiation of HMAC with MD5 from an instantiation with a random function with 2⁹⁷ queries with probability 0.87.

In 2011 an informational RFC 6151 was published to summarize security considerations in MD5 and HMAC-MD5. For HMAC-MD5 the RFC summarizes that – although the security of the MD5 hash function itself is severely compromised – the currently known "attacks on HMAC-MD5 do not seem to indicate a practical vulnerability when used as a message authentication code", but it also adds that "for a new protocol design, a ciphersuite with HMAC-MD5 should not be included".

In May 2011, RFC 6234 was published detailing the abstract theory and source code for SHA-based HMACs.

Examples

Here are some HMAC values, assuming 8-bit ASCII encoding:

HMAC_MD5("key", "The quick brown fox jumps over the lazy dog")    = 80070713463e7749b90c2dc24911e275

HMAC_SHA1("key", "The quick brown fox jumps over the lazy dog")   = de7c9b85b8b78aa6bc8a7a36f70a90701c9db4d9

HMAC_SHA256("key", "The quick brown fox jumps over the lazy dog") = f7bc83f430538424b13298e6aa6fb143ef4d59a14946175997479dbc2d1a3cd8

HMAC_SHA512("key", "The quick brown fox jumps over the lazy dog") = b42af09057bac1e2d41708e48a902e09b5ff7f12ab428a4fe86653c73dd248fb82f948a549f7b791a5b41915ee4d1ec3935357e4e2317250d0372afa2ebeeb3a

External links

• RFC2104
• Online HMAC Generator / Tester Tool
• FIPS PUB 198-1, The Keyed-Hash Message Authentication Code (HMAC)
• C HMAC implementation
• Python HMAC implementation
• Java implementation
• Rust HMAC implementation