CBC-MAC
In cryptography, a cipher block chaining message authentication code (CBC-MAC) is a technique for constructing a message authentication code (MAC) from a block cipher. The message is encrypted with some block cipher algorithm in cipher block chaining (CBC) mode to create a chain of blocks such that each block depends on the proper encryption of the previous block. This interdependence ensures that a change to any of the plaintext bits will cause the final encrypted block to change in a way that cannot be predicted or counteracted without knowing the key to the block cipher.
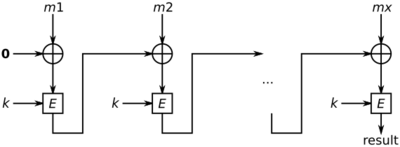
To calculate the CBC-MAC of message m, one encrypts m in CBC mode with zero initialization vector and keeps the last block. The following figure sketches the computation of the CBC-MAC of a message comprising blocks using a secret key k and a block cipher E:
CBC-MAC on its own is not secure for variable-length messages[1] (see the discussion below) and is currently used to construct a pseudorandom function family[2] and as a component of the CCM mode.
Use in standards
The CBC-MAC construct is used as part of the CCM mode utilized in IEEE 802.11i and NIST SP 800-97 (as CCMP, the CCM encryption protocol for WPA2), IPsec,[3] and TLS 1.2,[4] as well as Bluetooth Low Energy (as of Bluetooth 4.0, see NIST SP 800-121 Rev2).[5] It is available for TLS 1.3, but not enabled by default in OpenSSL.[6]
CBC-MAC is also used as a "conditioning component" (a.k.a. randomness extractor,[2] a method to generate bitstrings with full entropy) in NIST SP 800-90B.
Standards that define the algorithm
FIPS PUB 113 Computer Data Authentication is a (now obsolete) U.S. government standard that specified the CBC-MAC algorithm using DES as the block cipher.
The CBC-MAC algorithm is also included into ANSI X9.9, ANSI X9.19, ISO 8731-1, and ISO/IEC 9797-1 MAC (Algorithm 1).[7]
Security with fixed and variable-length messages
If the block cipher used is secure (meaning that it is a pseudorandom permutation), then CBC-MAC is secure for fixed-length messages.[1] However, by itself, it is not secure for variable-length messages. Thus, any single key must only be used for messages of a fixed and known length. This is because an attacker who knows the correct authentication tag (i.e. CBC-MAC) pairs for two messages and can generate a third message whose CBC-MAC will also be . This is simply done by XORing the first block of with t and then concatenating m with this modified ; i.e., by making . When computing the MAC for the message , it follows that we compute the MAC for m in the usual manner as t, but when this value is chained forwards to the stage computing we will perform an exclusive OR operation with the value derived for the MAC of the first message. The presence of that tag in the new message means it will cancel, leaving no contribution to the MAC from the blocks of plain text in the first message m: and thus the tag for is .
This problem cannot be solved by adding a message-size block to the end.[8] There are three main ways of modifying CBC-MAC so that it is secure for variable length messages: 1) Input-length key separation; 2) Length-prepending; 3) Encrypt last block.[8] In such a case, it may also be recommended to use a different mode of operation, for example, CMAC or HMAC to protect the integrity of variable-length messages.
Length prepending
One solution is to include the length of the message in the first block;[9] in fact CBC-MAC has been proven secure as long as no two messages that are prefixes of each other are ever used and prepending the length is a special case of this.[10] This can be problematic if the message length may not be known when processing begins.
Encrypt-last-block

Encrypt-last-block CBC-MAC (ECBC-MAC)[11] is defined as CBC-MAC-ELB(m, (k1, k2)) = E(k2, CBC-MAC(k1, m)).[8] Compared to the other discussed methods of extending CBC-MAC to variable-length messages, encrypt-last-block has the advantage of not needing to know the length of the message until the end of the computation.
Attack methods against incorrect use
As with many cryptographic schemes, naïve use of ciphers and other protocols may lead to attacks being possible, reducing the effectiveness of the cryptographic protection (or even rendering it useless). We present attacks which are possible due to using the CBC-MAC incorrectly.[12]
Using the same key for encryption and authentication
One common mistake is to reuse the same key k for CBC encryption and CBC-MAC. Although a reuse of a key for different purposes is a bad practice in general, in this particular case the mistake leads to a spectacular attack:
Suppose Alice has sent to Bob the cipher text blocks . During the transmission process, Eve can tamper with any of the cipher-text blocks and adjust any of the bits therein as she chooses, provided that the final block, , remains the same. We assume, for the purposes of this example and without loss of generality, that the initialization vector used for the encryption process is a vector of zeroes.
When Bob receives the message, he will first decrypt the message by reversing the encryption process which Alice applied, using the cipher text blocks . The tampered message, delivered to Bob in replacement of Alice's original, is .
Bob first decrypts the message received using the shared secret key K to obtain corresponding plain text. Note that all plain text produced will be different from that which Alice originally sent, because Eve has modified all but the last cipher text block. In particular, the final plain text, , differs from the original, , which Alice sent; although is the same, , so a different plain text is produced when chaining the previous cipher text block into the exclusive-OR after decryption of : .
It follows that Bob will now compute the authentication tag using CBC-MAC over all the values of plain text which he decoded. The tag for the new message, , is given by:
Notice that this expression is equal to
which is exactly :
and it follows that .
Therefore, Eve was able to modify the cipher text in transit (without necessarily knowing what plain text it corresponds to) such that an entirely different message, , was produced, but the tag for this message matched the tag of the original, and Bob was unaware that the contents had been modified in transit. By definition, a Message Authentication Code is broken if we can find a different message (a sequence of plain-text pairs ) which produces the same tag as the previous message, P, with . It follows that the message authentication protocol, in this usage scenario, has been broken, and Bob has been deceived into believing Alice sent him a message which she did not produce.
If, instead, we use different keys for the encryption and authentication stages, say and , respectively, this attack is foiled. The decryption of the modified cipher-text blocks obtains some plain text string . However, due to the MAC's usage of a different key , we cannot "undo" the decryption process in the forward step of the computation of the message authentication code so as to produce the same tag; each modified will now be encrypted by in the CBC-MAC process to some value .
This example also shows that a CBC-MAC cannot be used as a collision-resistant one-way function: given a key it is trivial to create a different message which "hashes" to the same tag.
Allowing the initialization vector to vary in value
When encrypting data using a block cipher in cipher block chaining (or another) mode, it is common to introduce an initialization vector to the first stage of the encryption process. It is typically required that this vector be chosen randomly (a nonce) and that it is not repeated for any given secret key under which the block cipher operates. This provides semantic security, by means of ensuring the same plain text is not encrypted to the same cipher text, allowing an attacker to infer a relationship exists.
When computing a message authentication code, such as by CBC-MAC, the use of an initialization vector is a possible attack vector.
In the operation of a ciphertext block chaining cipher, the first block of plain text is mixed with the initialization vector using an exclusive OR (). The result of this operation is the input to the block cipher for encryption.
However, when performing encryption and decryption, we are required to send the initialization vector in plain text - typically as the block immediately preceding the first block of cipher text - such that the first block of plain text can be decrypted and recovered successfully. If computing a MAC, we will also need to transmit the initialization vector to the other party in plain text so that they can verify the tag on the message matches the value they have computed.
If we allow the initialization vector to be selected arbitrarily, it follows that the first block of plain text can potentially be modified (transmitting a different message) while producing the same message tag.
Consider a message . In particular, when computing the message tag for CBC-MAC, suppose we choose an initialization vector such that computation of the MAC begins with . This produces a (message, tag) pair .
Now produce the message . For each bit modified in , flip the corresponding bit in the initialization vector to produce the initialization vector . It follows that to compute the MAC for this message, we begin the computation by . As bits in both the plain text and initialization vector have been flipped in the same places, the modification is cancelled in this first stage, meaning the input to the block cipher is identical to that for . If no further changes are made to the plain text, the same tag will be derived despite a different message being transmitted.
If the freedom to select an initialization vector is removed and all implementations of CBC-MAC fix themselves on a particular initialization vector (often the vector of zeroes, but in theory, it could be anything provided all implementations agree), this attack cannot proceed.
To sum up, if the attacker is able to set the IV that will be used for MAC verification, he can perform arbitrary modification of the first data block without invalidating the MAC.
Using predictable initialization vector
Sometimes IV is used as a counter to prevent message replay attacks. However, if the attacker can predict what IV will be used for MAC verification, he or she can replay previously observed message by modifying the first data block to compensate for the change in the IV that will be used for the verification. For example, if the attacker has observed message with and knows , he can produce that will pass MAC verification with .
The simplest countermeasure is to encrypt the IV before using it (i.e., prepending IV to the data). Alternatively MAC in CFB mode can be used, because in CFB mode the IV is encrypted before it is XORed with the data.
Another solution (in case protection against message replay attacks is not required) is to always use a zero vector IV.[13] Note that the above formula for becomes . So since and are the same message, by definition they will have the same tag. This is not a forgery, rather the intended use of CBC-MAC.
See also
- CMAC – A block-cipher–based MAC algorithm which is secure for messages of different lengths (recommended by NIST).
- OMAC and PMAC – Other methods to turn block ciphers into message authentication codes (MACs).
- One-way compression function – Hash functions can be made from block ciphers. But note, there are significant differences in function and uses for security between MACs (such as CBC-MAC) and hashes.
References
- ↑ 1.0 1.1 M. Bellare, J. Kilian and P. Rogaway. The security of the cipher block chaining message authentication code. JCSS 61(3):362–399, 2000.
- ↑ 2.0 2.1 Cliff, Boyd & Gonzalez Nieto 2009, p. 5.
- ↑ RFC 4309 Using Advanced Encryption Standard (AES) CCM Mode with IPsec Encapsulating Security Payload (ESP)
- ↑ RFC 6655 AES-CCM Cipher Suites for Transport Layer Security (TLS)
- ↑ "Bluetooth Low Energy Security". https://www.bluetooth.com/~/media/files/specification/bluetooth-low-energy-security.ashx?la=en.
- ↑ Caswell, Matt (2017-05-04). "Using TLS1.3 With OpenSSL". OpenSSL blog. https://www.openssl.org/blog/blog/2017/05/04/tlsv1.3/.
- ↑ Preneel & van Oorschot 1999, p. 7.
- ↑ 8.0 8.1 8.2 See Section 5 of Bellare, et al.
- ↑ ISO/IEC 9797-1:1999 Information technology – Security techniques – Message Authentication Codes (MACs) – Part 1: Mechanisms using a block cipher, clause 6.1.3 Padding Method 3
- ↑ C. Rackoff and S. Gorbunov. On the Security of Block Chaining Message Authentication Code.
- ↑ http://spark-university.s3.amazonaws.com/stanford-crypto/slides/05.3-integrity-cbc-mac-and-nmac.pptx [bare URL]
- ↑ Why I hate CBC-MAC by Matthew D. Green
- ↑ Introduction to Modern Cryptography, Second Edition by Jonathan Katz and Yehuda Lindell
Sources
- Cliff, Yvonne; Boyd, Colin; Gonzalez Nieto, Juan (2009). "How to Extract and Expand Randomness: A Summary and Explanation of Existing Results". Applied Cryptography and Network Security. Lecture Notes in Computer Science. 5536. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 53–70. doi:10.1007/978-3-642-01957-9_4. ISBN 978-3-642-01956-2. https://eprint.iacr.org/2009/136.pdf.
- Preneel, B.; van Oorschot, P.C. (1999). "On the security of iterated message authentication codes". IEEE Transactions on Information Theory (Institute of Electrical and Electronics Engineers (IEEE)) 45 (1): 188–199. doi:10.1109/18.746787. ISSN 0018-9448. http://cr.yp.to/bib/1999/preneel.pdf.
 |
