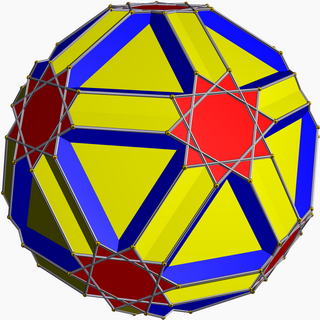
Icositruncated dodecadodecahedron
| Icositruncated dodecadodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 44, E = 180 V = 120 (χ = −16) |
| Faces by sides | 20{6}+12{10}+12{10/3} |
| Wythoff symbol | 3 5 5/3 | |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U45, C57, W84 |
| Dual polyhedron | Tridyakis icosahedron |
| Vertex figure | 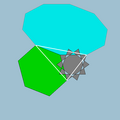 6.10.10/3 |
| Bowers acronym | Idtid |
File:Icositruncated dodecadodecahedron.stl In geometry, the icositruncated dodecadodecahedron or icosidodecatruncated icosidodecahedron is a nonconvex uniform polyhedron, indexed as U45.
Convex hull
Its convex hull is a nonuniform truncated icosidodecahedron.
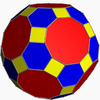 Truncated icosidodecahedron |
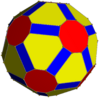 Convex hull |
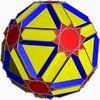Icositruncated dodecadodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of an icositruncated dodecadodecahedron are all the even permutations of [math]\displaystyle{ \begin{array}{crrlc} \Bigl(& \pm\bigl[2-\frac{1}{\varphi}\bigr],& \pm\,1,& \pm\bigl[2+\varphi\bigr] &\Bigr), \\ \Bigl(& \pm\,1,& \pm\,\frac{1}{\varphi^2},& \pm\bigl[3\varphi-1\bigr] &\Bigr), \\ \Bigl(& \pm\,2,& \pm\,\frac{2}{\varphi},& \pm\,2\varphi &\Bigr), \\ \Bigl(& \pm\,3,& \pm\,\frac{1}{\varphi^2},& \pm\,\varphi^2 &\Bigr), \\ \Bigl(& \pm\,\varphi^2,& \pm\,1,& \pm\bigl[3\varphi-2\bigr] &\Bigr), \end{array} }[/math]
where [math]\displaystyle{ \varphi = \tfrac{1+\sqrt 5}{2} }[/math] is the golden ratio.
Related polyhedra
Tridyakis icosahedron
| Tridyakis icosahedron | |
|---|---|
| |
| Type | Star polyhedron |
| Face |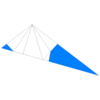 
|
| Elements | F = 120, E = 180 V = 44 (χ = −16) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | DU45 |
| dual polyhedron | Icositruncated dodecadodecahedron |
The tridyakis icosahedron is the dual polyhedron of the icositruncated dodecadodecahedron. It has 44 vertices, 180 edges, and 120 scalene triangular faces.
See also
- Catalan solid Duals to convex uniform polyhedra
- Uniform polyhedra
- List of uniform polyhedra
References
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5 Photo on page 96, Dorman Luke construction and stellation pattern on page 97.
External links
- Weisstein, Eric W.. "Icositruncated dodecadodecahedron". http://mathworld.wolfram.com/IcositruncatedDodecadodecahedron.html.
 |  |
