List of window functions

From HandWiki

In discrete-time signal processing, windowing is a preliminary signal shaping technique, usually applied to improve the appearance and usefulness of a subsequent Discrete Fourier Transform. Several window functions can be defined, based on a constant (rectangular window), B-splines, other polynomials, sinusoids, cosine-sums, adjustable, hybrid, and other types. The windowing operation consists of multiplying the given sampled signal by the window function.

Conventions

  • [math]\displaystyle{ w_0(x) }[/math] is a zero-phase function (symmetrical about [math]\displaystyle{ x=0 }[/math]),[1] continuous for [math]\displaystyle{ x \in [-N/2, N/2], }[/math] where [math]\displaystyle{ N }[/math] is a positive integer (even or odd).[2]
  • The sequence  [math]\displaystyle{ \{w[n] = w_0(n-N/2),\quad 0\le n \le N\} }[/math]  is symmetric, of length [math]\displaystyle{ N+1. }[/math]
  • [math]\displaystyle{ \{w[n],\quad 0\le n \le N-1\} }[/math]  is DFT-symmetric, of length [math]\displaystyle{ N. }[/math][upper-alpha 1]
  • The parameter B displayed on each spectral plot is the function's noise equivalent bandwidth metric, in units of DFT bins.

The sparse sampling of a DTFT (such as the DFTs in Fig 2) only reveals the leakage into the DFT bins from a sinusoid whose frequency is also an integer DFT bin. The unseen sidelobes reveal the leakage to expect from sinusoids at other frequencies.[lower-alpha 1] Therefore, when choosing a window function, it is usually important to sample the DTFT more densely (as we do throughout this section) and choose a window that suppresses the sidelobes to an acceptable level.

Rectangular window

Rectangular window

The rectangular window (sometimes known as the boxcar or Dirichlet window) is the simplest window, equivalent to replacing all but N values of a data sequence by zeros, making it appear as though the waveform suddenly turns on and off:

[math]\displaystyle{ w[n] = 1. }[/math]

Other windows are designed to moderate these sudden changes, which reduces scalloping loss and improves dynamic range, as described above (§ Spectral analysis).

The rectangular window is the 1st order B-spline window as well as the 0th power power-of-sine window.

The rectangular window provides the minimum mean square error estimate of the Discrete-time Fourier transform, at the cost of other issues discussed.

B-spline windows

B-spline windows can be obtained as k-fold convolutions of the rectangular window. They include the rectangular window itself (k = 1), the § Triangular window (k = 2) and the § Parzen window (k = 4).[5] Alternative definitions sample the appropriate normalized B-spline basis functions instead of convolving discrete-time windows.  A  kth-order B-spline basis function is a piece-wise polynomial function of degree k−1 that is obtained by k-fold self-convolution of the rectangular function.

Triangular window

Triangular window (with L = N + 1)

Triangular windows are given by:

[math]\displaystyle{ w[n] = 1 - \left|\frac{n-\frac{N}{2}}{\frac{L}{2}}\right|,\quad 0\le n \le N }[/math]

where L can be N,[6] N + 1,[3] [7][8] or N + 2.[9]  The first one is also known as Bartlett window or Fejér window. All three definitions converge at large N.

The triangular window is the 2nd order B-spline window. The L = N form can be seen as the convolution of two N/2-width rectangular windows. The Fourier transform of the result is the squared values of the transform of the half-width rectangular window.

Parzen window

Parzen window

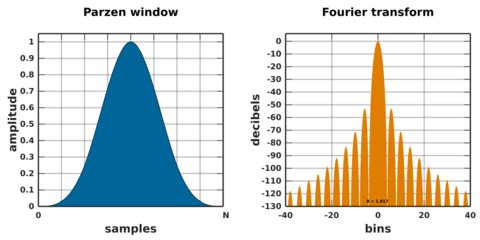
Defining  L ≜ N + 1,  the Parzen window, also known as the de la Vallée Poussin window,[3] is the 4th order B-spline window given by:

[math]\displaystyle{ w_0(n) \triangleq \left\{ \begin{array}{ll} 1 - 6 \left(\frac{n}{L/2}\right)^2 \left(1 - \frac{|n|}{L/2}\right), & 0 \le |n| \le \frac{L}{4} \\ 2 \left(1 - \frac{|n|}{L/2}\right)^3 & \frac{L}{4} \lt |n| \le \frac{L}{2} \\ \end{array} \right\} }[/math]
[math]\displaystyle{ w[n] = \ w_0\left(n-\tfrac{N}{2}\right),\ 0 \le n \le N }[/math]
Welch window

Other polynomial windows

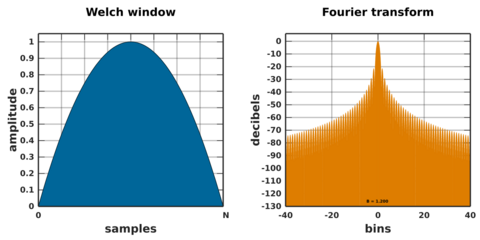
Welch window

The Welch window consists of a single parabolic section:

[math]\displaystyle{ w[n]=1 - \left(\frac{n-\frac{N}{2}}{\frac{N}{2}}\right)^2,\quad 0\le n \le N. }[/math][9]

The defining quadratic polynomial reaches a value of zero at the samples just outside the span of the window.

Sine window

Sine window
[math]\displaystyle{ w[n] = \sin\left(\frac{\pi n}{N}\right) = \cos\left(\frac{\pi n}{N} - \frac{\pi}{2}\right),\quad 0\le n \le N. }[/math]

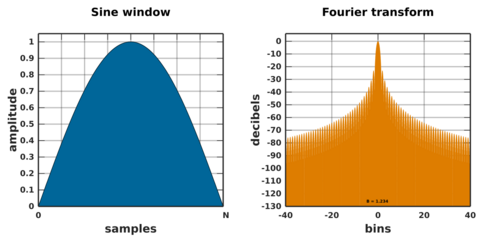
The corresponding [math]\displaystyle{ w_0(n)\, }[/math] function is a cosine without the π/2 phase offset. So the sine window[10] is sometimes also called cosine window.[3] As it represents half a cycle of a sinusoidal function, it is also known variably as half-sine window[11] or half-cosine window.[12]

The autocorrelation of a sine window produces a function known as the Bohman window.[13]

Power-of-sine/cosine windows

These window functions have the form:[14]

[math]\displaystyle{ w[n] = \sin^\alpha\left(\frac{\pi n}{N}\right) = \cos^\alpha\left(\frac{\pi n}{N} - \frac{\pi}{2}\right),\quad 0\le n \le N. }[/math]

The rectangular window (α = 0), the sine window (α = 1), and the Hann window (α = 2) are members of this family.

For even-integer values of α these functions can also be expressed in cosine-sum form:

[math]\displaystyle{ w[n]=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N} \right)- a_3 \cos \left ( \frac{6 \pi n}{N} \right)+ a_4 \cos \left ( \frac{8 \pi n}{N} \right)- ... }[/math]
[math]\displaystyle{ \begin{array}{l|llll} \hline \alpha & a_0 & a_1 & a_2 & a_3 & a_4 \\ \hline 0 & 1 \\ 2 & 0.5 & 0.5 \\ 4 & 0.375 & 0.5 & 0.125 \\ 6 & 0.3125 & 0.46875 & 0.1875 & 0.03125 \\ 8 & 0.2734375 & 0.4375 & 0.21875 & 0.0625 & 7.8125\times10^{-3} \\ \hline \end{array} }[/math]

Cosine-sum windows

This family is also known as generalized cosine windows.

[math]\displaystyle{ w[n] = \sum_{k = 0}^{K} (-1)^k a_k\; \cos\left( \frac{2 \pi k n}{N} \right),\quad 0\le n \le N. }[/math]

 

 

 

 

(Eq.1)

In most cases, including the examples below, all coefficients ak ≥ 0.  These windows have only 2K + 1 non-zero N-point DFT coefficients.

Hann and Hamming windows

Main page: Hann function
Hann window
Hamming window, a0 = 0.53836 and a1 = 0.46164. The original Hamming window would have a0 = 0.54 and a1 = 0.46.

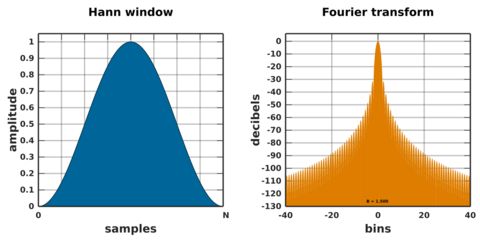
The customary cosine-sum windows for case K = 1 have the form:

[math]\displaystyle{ w[n] = a_0 - \underbrace{(1-a_0)}_{a_1}\cdot \cos\left( \tfrac{2 \pi n}{N} \right),\quad 0\le n \le N, }[/math]

which is easily (and often) confused with its zero-phase version:

[math]\displaystyle{ \begin{align} w_0(n)\ &= w\left[ n+\tfrac{N}{2}\right]\\ &= a_0 + a_1\cdot \cos \left ( \tfrac{2\pi n}{N} \right),\quad -\tfrac{N}{2} \le n \le \tfrac{N}{2}. \end{align} }[/math]

Setting  [math]\displaystyle{ a_0 = 0.5 }[/math]  produces a Hann window:

[math]\displaystyle{ w[n] = 0.5\; \left[1 - \cos \left ( \frac{2 \pi n}{N} \right) \right] = \sin^2 \left ( \frac{\pi n}{N} \right), }[/math][15]

named after Julius von Hann, and sometimes erroneously referred to as Hanning, presumably due to its linguistic and formulaic similarities to the Hamming window. It is also known as raised cosine, because the zero-phase version, [math]\displaystyle{ w_0(n), }[/math] is one lobe of an elevated cosine function.

This function is a member of both the cosine-sum and power-of-sine families. Unlike the Hamming window, the end points of the Hann window just touch zero. The resulting side-lobes roll off at about 18 dB per octave.[16]

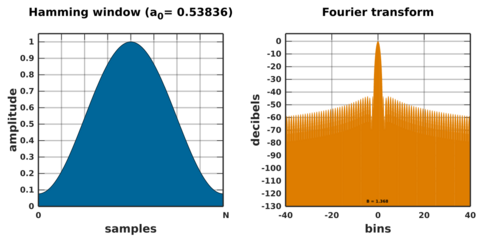
Setting  [math]\displaystyle{ a_0 }[/math]  to approximately 0.54, or more precisely 25/46, produces the Hamming window, proposed by Richard W. Hamming. That choice places a zero-crossing at frequency 5π/(N − 1), which cancels the first sidelobe of the Hann window, giving it a height of about one-fifth that of the Hann window.[3][17][18] The Hamming window is often called the Hamming blip when used for pulse shaping.[19][20][21]

Approximation of the coefficients to two decimal places substantially lowers the level of sidelobes,[3] to a nearly equiripple condition.[18] In the equiripple sense, the optimal values for the coefficients are a0 = 0.53836 and a1 = 0.46164.[18][22]

Blackman window

Blackman window; α = 0.16

Blackman windows are defined as:

[math]\displaystyle{ w[n] = a_0 - a_1 \cos \left ( \frac{2 \pi n}{N} \right) + a_2 \cos \left ( \frac{4 \pi n}{N} \right) }[/math]
[math]\displaystyle{ a_0=\frac{1-\alpha}{2};\quad a_1=\frac{1}{2};\quad a_2=\frac{\alpha}{2}. }[/math]

By common convention, the unqualified term Blackman window refers to Blackman's "not very serious proposal" of α = 0.16 (a0 = 0.42, a1 = 0.5, a2 = 0.08), which closely approximates the exact Blackman,[23] with a0 = 7938/18608 ≈ 0.42659, a1 = 9240/18608 ≈ 0.49656, and a2 = 1430/18608 ≈ 0.076849.[24] These exact values place zeros at the third and fourth sidelobes,[3] but result in a discontinuity at the edges and a 6 dB/oct fall-off. The truncated coefficients do not null the sidelobes as well, but have an improved 18 dB/oct fall-off.[3][25]

Nuttall window, continuous first derivative

Nuttall window, continuous first derivative

The continuous form of the Nuttall window, [math]\displaystyle{ w_0(x), }[/math] and its first derivative are continuous everywhere, like the Hann function. That is, the function goes to 0 at x = ±N/2, unlike the Blackman–Nuttall, Blackman–Harris, and Hamming windows. The Blackman window (α = 0.16) is also continuous with continuous derivative at the edge, but the "exact Blackman window" is not.

[math]\displaystyle{ w[n]=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N} \right)- a_3 \cos \left ( \frac{6 \pi n}{N} \right) }[/math]
[math]\displaystyle{ a_0=0.355768;\quad a_1=0.487396;\quad a_2=0.144232;\quad a_3=0.012604. }[/math]

Blackman–Nuttall window

Blackman–Nuttall window
[math]\displaystyle{ w[n]=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N} \right)- a_3 \cos \left ( \frac{6 \pi n}{N} \right) }[/math]
[math]\displaystyle{ a_0=0.3635819; \quad a_1=0.4891775; \quad a_2=0.1365995; \quad a_3=0.0106411. }[/math]

Blackman–Harris window

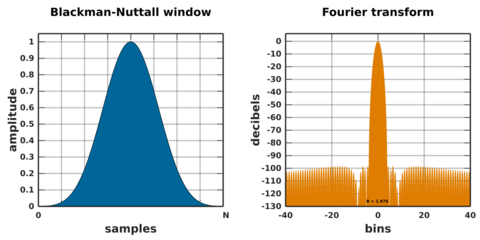
Blackman–Harris window

A generalization of the Hamming family, produced by adding more shifted sinc functions, meant to minimize side-lobe levels[26][27]

[math]\displaystyle{ w[n]=a_0 - a_1 \cos \left ( \frac{2 \pi n}{N} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N} \right)- a_3 \cos \left ( \frac{6 \pi n}{N} \right) }[/math]
[math]\displaystyle{ a_0=0.35875;\quad a_1=0.48829;\quad a_2=0.14128;\quad a_3=0.01168. }[/math]

Flat top window

Flat-top window

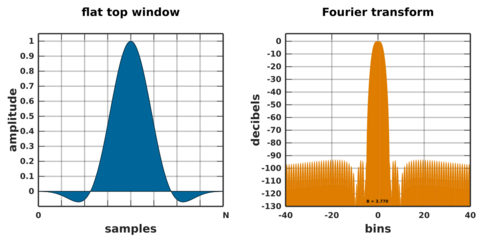
A flat top window is a partially negative-valued window that has minimal scalloping loss in the frequency domain. That property is desirable for the measurement of amplitudes of sinusoidal frequency components.[4][28] Drawbacks of the broad bandwidth are poor frequency resolution and high § Noise bandwidth.

Flat top windows can be designed using low-pass filter design methods,[28] or they may be of the usual cosine-sum variety:

[math]\displaystyle{ \begin{align} w[n] = a_0 &{}- a_1 \cos \left ( \frac{2 \pi n}{N} \right)+ a_2 \cos \left ( \frac{4 \pi n}{N} \right)\\ &{}- a_3 \cos \left ( \frac{6 \pi n}{N} \right)+a_4 \cos \left ( \frac{8 \pi n}{N} \right). \end{align} }[/math]

The Matlab variant has these coefficients:

[math]\displaystyle{ a_0=0.21557895;\quad a_1=0.41663158;\quad a_2=0.277263158;\quad a_3=0.083578947;\quad a_4=0.006947368. }[/math]

Other variations are available, such as sidelobes that roll off at the cost of higher values near the main lobe.[4]

Rife–Vincent windows

Rife–Vincent windows[29] are customarily scaled for unity average value, instead of unity peak value. The coefficient values below, applied to Eq.1, reflect that custom.

Class I, Order 1 (K = 1):  [math]\displaystyle{ a_0=1;\quad a_1=1 }[/math]       Functionally equivalent to the Hann window.

Class I, Order 2 (K = 2):  [math]\displaystyle{ a_0=1;\quad a_1=\tfrac{4}{3};\quad a_2=\tfrac{1}{3} }[/math]

Class I is defined by minimizing the high-order sidelobe amplitude. Coefficients for orders up to K=4 are tabulated.[30]

Class II minimizes the main-lobe width for a given maximum side-lobe.

Class III is a compromise for which order K = 2 resembles the § Blackman window.[30][31]

Adjustable windows

Gaussian window

Gaussian window, σ = 0.4

The Fourier transform of a Gaussian is also a Gaussian. Since the support of a Gaussian function extends to infinity, it must either be truncated at the ends of the window, or itself windowed with another zero-ended window.[32]

Since the log of a Gaussian produces a parabola, this can be used for nearly exact quadratic interpolation in frequency estimation.[33][32][34]

[math]\displaystyle{ w[n]=\exp\left(-\frac{1}{2} \left ( \frac{n-N/2}{\sigma N/2} \right)^{2}\right),\quad 0\le n \le N. }[/math]
[math]\displaystyle{ \sigma \le \;0.5\, }[/math]

The standard deviation of the Gaussian function is σ · N/2 sampling periods.

Confined Gaussian window, σt = 0.1

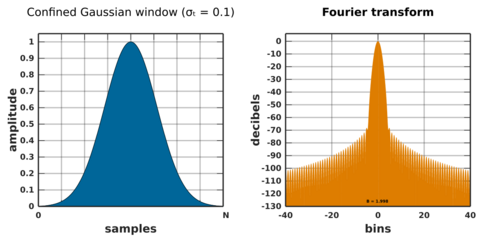
Confined Gaussian window

The confined Gaussian window yields the smallest possible root mean square frequency width σω for a given temporal width  (N + 1) σt.[35] These windows optimize the RMS time-frequency bandwidth products. They are computed as the minimum eigenvectors of a parameter-dependent matrix. The confined Gaussian window family contains the § Sine window and the § Gaussian window in the limiting cases of large and small σt, respectively.

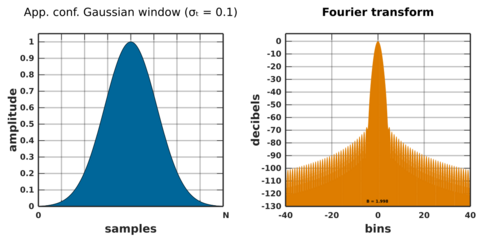
Approximate confined Gaussian window, σt = 0.1

Approximate confined Gaussian window

Defining  L ≜ N + 1,  a confined Gaussian window of temporal width  L × σt  is well approximated by:[35]

[math]\displaystyle{ w[n] = G(n) - \frac{G(-\tfrac{1}{2})[G(n + L) + G(n - L)]}{G(-\tfrac{1}{2} + L) + G(-\tfrac{1}{2} - L)} }[/math]

where [math]\displaystyle{ G }[/math] is a Gaussian function:

[math]\displaystyle{ G(x) = \exp\left(- \left(\cfrac{x - \frac{N}{2}}{2 L \sigma_t}\right)^2\right) }[/math]

The standard deviation of the approximate window is asymptotically equal (i.e. large values of N) to  L × σt  for  σt < 0.14.[35]

Generalized normal window

A more generalized version of the Gaussian window is the generalized normal window.[36] Retaining the notation from the Gaussian window above, we can represent this window as

[math]\displaystyle{ w[n,p]=\exp\left(-\left ( \frac{n-N/2}{\sigma N/2} \right)^{p}\right) }[/math]

for any even [math]\displaystyle{ p }[/math]. At [math]\displaystyle{ p=2 }[/math], this is a Gaussian window and as [math]\displaystyle{ p }[/math] approaches [math]\displaystyle{ \infty }[/math], this approximates to a rectangular window. The Fourier transform of this window does not exist in a closed form for a general [math]\displaystyle{ p }[/math]. However, it demonstrates the other benefits of being smooth, adjustable bandwidth. Like the § Tukey window, this window naturally offers a "flat top" to control the amplitude attenuation of a time-series (on which we don't have a control with Gaussian window). In essence, it offers a good (controllable) compromise, in terms of spectral leakage, frequency resolution and amplitude attenuation, between the Gaussian window and the rectangular window. See also [37] for a study on time-frequency representation of this window (or function).

Tukey window

Tukey window, α = 0.5

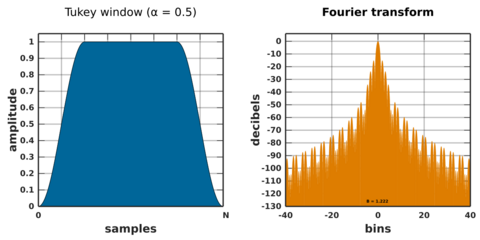
The Tukey window, also known as the cosine-tapered window, can be regarded as a cosine lobe of width Nα/2 (spanning Nα/2 + 1 observations) that is convolved with a rectangular window of width N(1 − α/2).

[math]\displaystyle{ \left . \begin{array}{lll} w[n] = \frac{1}{2} \left[1-\cos \left(\frac{2\pi n}{\alpha N} \right) \right],\quad & 0 \le n \lt \frac{\alpha N}{2}\\ w[n] = 1,\quad & \frac{\alpha N}{2} \le n \le \frac{N}{2}\\ w[N-n] = w[n],\quad & 0 \le n \le \frac{N}{2} \end{array}\right\} }[/math]  [38][upper-alpha 2][upper-alpha 3]

At α = 0 it becomes rectangular, and at α = 1 it becomes a Hann window.

Planck-taper window

Planck-taper window, ε = 0.1

The so-called "Planck-taper" window is a bump function that has been widely used[39] in the theory of partitions of unity in manifolds. It is smooth (a [math]\displaystyle{ C^\infty }[/math] function) everywhere, but is exactly zero outside of a compact region, exactly one over an interval within that region, and varies smoothly and monotonically between those limits. Its use as a window function in signal processing was first suggested in the context of gravitational-wave astronomy, inspired by the Planck distribution.[40] It is defined as a piecewise function:

[math]\displaystyle{ \left . \begin{array}{lll} w[0] = 0, \\ w[n] = \left(1 + \exp\left(\frac{\varepsilon N}{n} - \frac{\varepsilon N}{\varepsilon N - n}\right)\right)^{-1},\quad & 1 \le n \lt \varepsilon N \\ w[n] = 1,\quad & \varepsilon N \le n \le \frac{N}{2} \\ w[N-n] = w[n],\quad & 0 \le n \le \frac{N}{2} \end{array}\right\} }[/math]

The amount of tapering is controlled by the parameter ε, with smaller values giving sharper transitions.

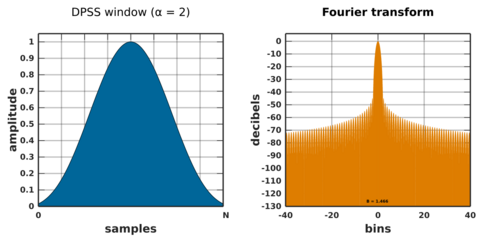
DPSS or Slepian window

The DPSS (discrete prolate spheroidal sequence) or Slepian window maximizes the energy concentration in the main lobe,[41] and is used in multitaper spectral analysis, which averages out noise in the spectrum and reduces information loss at the edges of the window.

The main lobe ends at a frequency bin given by the parameter α.[42]

DPSS window, α = 2
DPSS window, α = 3

The Kaiser windows below are created by a simple approximation to the DPSS windows:

Kaiser window, α = 2
Kaiser window, α = 3

Kaiser window

Main page: Kaiser window

The Kaiser, or Kaiser–Bessel, window is a simple approximation of the DPSS window using Bessel functions, discovered by James Kaiser.[43][44]

[math]\displaystyle{ w[n]=\frac{I_0\left(\pi\alpha \sqrt{1-\left(\frac{2 n}{N}-1\right)^2}\right)}{I_0(\pi\alpha)},\quad 0\le n \le N }[/math]    [upper-alpha 4][3]:p. 73
[math]\displaystyle{ w_0(n) = \frac{I_0\left(\pi\alpha \sqrt{1-\left(\frac{2 n}{N}\right)^2}\right)}{I_0(\pi\alpha)},\quad -N/2 \le n \le N/2 }[/math]

where [math]\displaystyle{ I_0 }[/math] is the zero-th order modified Bessel function of the first kind. Variable parameter [math]\displaystyle{ \alpha }[/math] determines the tradeoff between main lobe width and side lobe levels of the spectral leakage pattern.  The main lobe width, in between the nulls, is given by  [math]\displaystyle{ 2\sqrt{1 + \alpha^2}, }[/math]  in units of DFT bins,[52]  and a typical value of [math]\displaystyle{ \alpha }[/math] is 3.

Dolph–Chebyshev window

Dolph–Chebyshev window, α = 5

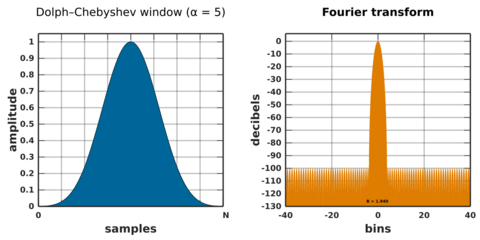
Minimizes the Chebyshev norm of the side-lobes for a given main lobe width.[53]

The zero-phase Dolph–Chebyshev window function [math]\displaystyle{ w_0[n] }[/math] is usually defined in terms of its real-valued discrete Fourier transform, [math]\displaystyle{ W_0[k] }[/math]:[54]

[math]\displaystyle{ W_0(k) = \frac{T_{N} \big(\beta \cos\left(\frac{\pi k}{N+1}\right)\big)}{T_{N} (\beta)} = \frac{T_N \big(\beta \cos\left(\frac{\pi k}{N+1}\right)\big)}{10^\alpha},\ 0 \le k \le N. }[/math]

Tn(x) is the n-th Chebyshev polynomial of the first kind evaluated in x, which can be computed using

[math]\displaystyle{ T_n(x) =\begin{cases} \cos\!\big(n \cos^{-1}(x) \big) & \text{if }-1 \le x \le 1 \\ \cosh\!\big(n \cosh^{-1}(x) \big) & \text{if }x \ge 1 \\ (-1)^n \cosh\!\big(n \cosh^{-1}(-x) \big) & \text{if }x \le -1, \end{cases} }[/math]

and

[math]\displaystyle{ \beta = \cosh\!\big(\tfrac{1}{N} \cosh^{-1}(10^\alpha)\big) }[/math]

is the unique positive real solution to [math]\displaystyle{ T_N(\beta) = 10^\alpha }[/math], where the parameter α sets the Chebyshev norm of the sidelobes to −20α decibels.[53]

The window function can be calculated from W0(k) by an inverse discrete Fourier transform (DFT):[53]

[math]\displaystyle{ w_0(n) = \frac{1}{N+1} \sum_{k=0}^N W_0(k) \cdot e^{i 2 \pi k n / (N+1)},\ -N/2 \le n \le N/2. }[/math]

The lagged version of the window can be obtained by:

[math]\displaystyle{ w[n] = w_0\left(n-\frac{N}{2}\right),\quad 0 \le n \le N, }[/math]

which for even values of N must be computed as follows:

[math]\displaystyle{ \begin{align} w_0\left(n-\frac{N}{2}\right) = \frac{1}{N+1} \sum_{k=0}^{N} W_0(k) \cdot e^{\frac{i 2 \pi k (n-N/2)}{N+1}} = \frac{1}{N+1} \sum_{k=0}^{N} \left[ \left(-e^{\frac{i\pi}{N+1}}\right)^k \cdot W_0(k)\right] e^{\frac{i 2 \pi k n}{N+1}}, \end{align} }[/math]

which is an inverse DFT of  [math]\displaystyle{ \left(-e^{\frac{i\pi}{N+1}}\right)^k\cdot W_0(k). }[/math]

Variations:

  • Due to the equiripple condition, the time-domain window has discontinuities at the edges. An approximation that avoids them, by allowing the equiripples to drop off at the edges, is a Taylor window.
  • An alternative to the inverse DFT definition is also available.[1].

Ultraspherical window

The Ultraspherical window's μ parameter determines whether its Fourier transform's side-lobe amplitudes decrease, are level, or (shown here) increase with frequency.

The Ultraspherical window was introduced in 1984 by Roy Streit[55] and has application in antenna array design,[56] non-recursive filter design,[55] and spectrum analysis.[57]

Like other adjustable windows, the Ultraspherical window has parameters that can be used to control its Fourier transform main-lobe width and relative side-lobe amplitude. Uncommon to other windows, it has an additional parameter which can be used to set the rate at which side-lobes decrease (or increase) in amplitude.[57][58][59]

The window can be expressed in the time-domain as follows:[57]

[math]\displaystyle{ w[n] = \frac{1}{N+1} \left[ C^\mu_N(x_0)+\sum_{k=1}^{\frac{N}{2}} C^\mu_N \left(x_0 \cos\frac{k\pi}{N+1}\right)\cos\frac{2n\pi k}{N+1} \right] }[/math]

where [math]\displaystyle{ C^{\mu}_{N} }[/math] is the Ultraspherical polynomial of degree N, and [math]\displaystyle{ x_0 }[/math] and [math]\displaystyle{ \mu }[/math] control the side-lobe patterns.[57]

Certain specific values of [math]\displaystyle{ \mu }[/math] yield other well-known windows: [math]\displaystyle{ \mu=0 }[/math] and [math]\displaystyle{ \mu=1 }[/math] give the Dolph–Chebyshev and Saramäki windows respectively.[55] See here for illustration of Ultraspherical windows with varied parametrization.

Exponential or Poisson window

Exponential window, τ = N/2
Exponential window, τ = (N/2)/(60/8.69)

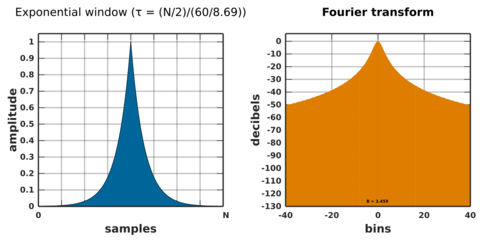
The Poisson window, or more generically the exponential window increases exponentially towards the center of the window and decreases exponentially in the second half. Since the exponential function never reaches zero, the values of the window at its limits are non-zero (it can be seen as the multiplication of an exponential function by a rectangular window [60]). It is defined by

[math]\displaystyle{ w[n]=e^{-\left|n-\frac{N}{2}\right|\frac{1}{\tau}}, }[/math]

where τ is the time constant of the function. The exponential function decays as e ≃ 2.71828 or approximately 8.69 dB per time constant.[61] This means that for a targeted decay of D dB over half of the window length, the time constant τ is given by

[math]\displaystyle{ \tau = \frac{N}{2}\frac{8.69}{D}. }[/math]

Hybrid windows

Window functions have also been constructed as multiplicative or additive combinations of other windows.

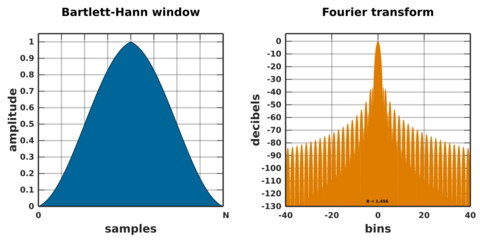
Bartlett–Hann window

Bartlett–Hann window

[math]\displaystyle{ w[n]=a_0 - a_1 \left |\frac{n}{N}-\frac{1}{2} \right| - a_2 \cos \left (\frac{2 \pi n}{N}\right ) }[/math]
[math]\displaystyle{ a_0=0.62;\quad a_1=0.48;\quad a_2=0.38\, }[/math]

Planck–Bessel window

Planck–Bessel window, ε = 0.1, α = 4.45

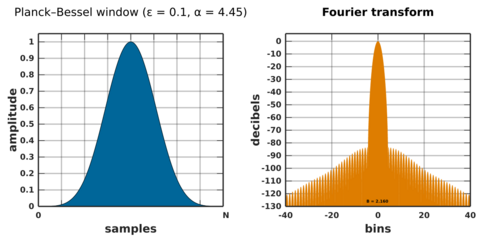
A § Planck-taper window multiplied by a Kaiser window which is defined in terms of a modified Bessel function. This hybrid window function was introduced to decrease the peak side-lobe level of the Planck-taper window while still exploiting its good asymptotic decay.[62] It has two tunable parameters, ε from the Planck-taper and α from the Kaiser window, so it can be adjusted to fit the requirements of a given signal.

Hann–Poisson window

Hann–Poisson window, α = 2

A Hann window multiplied by a Poisson window. For [math]\displaystyle{ \alpha \geqslant 2 }[/math] it has no side-lobes, as its Fourier transform drops off forever away from the main lobe without local minima. It can thus be used in hill climbing algorithms like Newton's method.[63] The Hann–Poisson window is defined by:

[math]\displaystyle{ w[n]=\frac{1}{2}\left(1-\cos\left(\frac{2 \pi n}{N}\right)\right)e^\frac{-\alpha\left|N - 2n\right|}{N}\, }[/math]

where α is a parameter that controls the slope of the exponential.

Other windows

GAP window (GAP optimized Nuttall window)

Generalized adaptive polynomial (GAP) window

The GAP window[64] is a family of adjustable window functions that are based on a symmetrical polynomial expansion of order [math]\displaystyle{ K }[/math]. It is continuous with continuous derivative everywhere. With the appropriate set of expansion coefficients and expansion order, the GAP window can mimic all the known window functions, reproducing accurately their spectral properties.

[math]\displaystyle{ w_0[n] = a_{0} + \sum_{k=1}^{K} a_{2k}\left(\frac{n}{\sigma}\right)^{2k}, \quad -\frac{N}{2} \le n \le \frac{N}{2}, }[/math]  [65]

where [math]\displaystyle{ \sigma }[/math] is the standard deviation of the [math]\displaystyle{ \{n\} }[/math] sequence.

Additionally, starting with a set of expansion coefficients [math]\displaystyle{ a_{2k} }[/math] that mimics a certain known window function, the GAP window can be optimized by minimization procedures to get a new set of coefficients that improve one or more spectral properties, such as the main lobe width, side lobe attenuation, and side lobe falloff rate.[66] Therefore, a GAP window function can be developed with designed spectral properties depending on the specific application.

Sinc or Lanczos window

Lanczos window

[math]\displaystyle{ w[n] = \operatorname{sinc}\left(\frac{2n}{N} - 1\right) }[/math]

  • used in Lanczos resampling
  • for the Lanczos window, [math]\displaystyle{ \operatorname{sinc}(x) }[/math] is defined as [math]\displaystyle{ \sin(\pi x)/\pi x }[/math]
  • also known as a sinc window, because: [math]\displaystyle{ w_0(n) = \operatorname{sinc}\left(\frac{2n}{N}\right)\, }[/math] is the main lobe of a normalized sinc function


Notes

  1. ↑ Some authors limit their attention to this important subset and to even values of N.[3][4] But the window coefficient formulas are still the ones presented here.
  2. ↑ This formula can be confirmed by simplifying the cosine function at MATLAB tukeywin and substituting r=α and x=n/N.
  3. ↑ Harris 1978 (p 67, eq 38) appears to have two errors: (1) The subtraction operator in the numerator of the cosine function should be addition. (2) The denominator contains a spurious factor of 2. Also, Fig 30 corresponds to α=0.25 using the Wikipedia formula, but to 0.75 using the Harris formula. Fig 32 is similarly mislabeled.
  4. ↑ The Kaiser window is often parametrized by β, where β = πα.[45][46] [47][48][42][49][50]:p. 474  The alternative use of just α facilitates comparisons to the DPSS windows.[51]

Page citations

  1. ↑ Harris 1978, p 57, fig 10.

References

  1. ↑ "Zero Phase Filters". https://ccrma.stanford.edu/~jos/filters/Zero_Phase_Filters_Even_Impulse.html. 
  2. ↑ Rorabaugh, C.Britton (October 1998). DSP Primer. Primer series. McGraw-Hill Professional. p. 196. ISBN 978-0070540040. 
  3. ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 Harris, Fredric J. (Jan 1978). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform". Proceedings of the IEEE 66 (1): 51–83. doi:10.1109/PROC.1978.10837. Bibcode: 1978IEEEP..66...51H. http://web.mit.edu/xiphmont/Public/windows.pdf.  The fundamental 1978 paper on FFT windows by Harris, which specified many windows and introduced key metrics used to compare them.
  4. ↑ 4.0 4.1 4.2 Heinzel, G.; Rüdiger, A.; Schilling, R. (2002). Spectrum and spectral density estimation by the Discrete Fourier transform (DFT), including a comprehensive list of window functions and some new flat-top windows (Technical report). Max Planck Institute (MPI) für Gravitationsphysik / Laser Interferometry & Gravitational Wave Astronomy. 395068.0. Retrieved 2013-02-10. Also available at https://pure.mpg.de/rest/items/item_152164_1/component/file_152163/content
  5. ↑ Toraichi, K.; Kamada, M.; Itahashi, S.; Mori, R. (1989). "Window functions represented by B-spline functions". IEEE Transactions on Acoustics, Speech, and Signal Processing 37: 145–147. doi:10.1109/29.17517. 
  6. ↑ "Bartlett Window". https://ccrma.stanford.edu/~jos/sasp/Bartlett_Triangular_Window.html. 
  7. ↑ Tukey, J.W. (1967). "An introduction to the calculations of numerical spectrum analysis". Spectral Analysis of Time Series: 25–46. 
  8. ↑ "Triangular window – MATLAB triang". http://www.mathworks.com/help/signal/ref/triang.html. 
  9. ↑ 9.0 9.1 Welch, P. (1967). "The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms". IEEE Transactions on Audio and Electroacoustics 15 (2): 70–73. doi:10.1109/TAU.1967.1161901. Bibcode: 1967ITAE...15...70W. 
  10. ↑ Bosi, Marina; Goldberg, Richard E. (2003). "Time to Frequency Mapping Part II: The MDCT". Introduction to Digital Audio Coding and Standards. The Springer International Series in Engineering and Computer Science. 721. Boston, MA: Springer US. p. 106. doi:10.1007/978-1-4615-0327-9. ISBN 978-1-4615-0327-9. 
  11. ↑ Kido, Ken'iti; Suzuki, Hideo; Ono, Takahiko; Fukushima, Manabu (1998). "Deformation of impulse response estimates by time window in cross spectral technique". Journal of the Acoustical Society of Japan (E) 19 (5): 349–361. doi:10.1250/ast.19.349. 
  12. ↑ Landisman, M.; Dziewonski, A.; Satô, Y. (1969-05-01). "Recent Improvements in the Analysis of Surface Wave Observations". Geophysical Journal International 17 (4): 369–403. doi:10.1111/j.1365-246X.1969.tb00246.x. Bibcode: 1969GeoJ...17..369L. 
  13. ↑ "Bohman window – R2019B". https://www.mathworks.com/help/signal/ref/bohmanwin.html. 
  14. ↑ "Power-of-Cosine Window Family". https://ccrma.stanford.edu/~jos/sasp/Power_of_Cosine_Window_Family.html. 
  15. ↑ "Hann (Hanning) window - MATLAB hann". http://www.mathworks.com/help/signal/ref/hann.html. 
  16. ↑ "Hann or Hanning or Raised Cosine". https://ccrma.stanford.edu/~jos/sasp/Hann_Hanning_Raised_Cosine.html. 
  17. ↑ Enochson, Loren D.; Otnes, Robert K. (1968). Programming and Analysis for Digital Time Series Data. U.S. Dept. of Defense, Shock and Vibration Info. Center. pp. 142. https://books.google.com/books?id=duBQAAAAMAAJ&q=%22hamming+window%22+date:0-1970. 
  18. ↑ 18.0 18.1 18.2 "Hamming Window". https://ccrma.stanford.edu/~jos/sasp/Hamming_Window.html. 
  19. ↑ "A digital quadrature amplitude modulation (QAM) Radio: Building a better radio". p. 28. https://users.wpi.edu/~sunar/courses/ece3311/slides/ch16.pdf. 
  20. ↑ "Bits to Symbols to Signals and back again". p. 7. https://users.wpi.edu/~sunar/courses/ece3311/slides/ch08.pdf. 
  21. ↑ Johnson, C.Richard, Jr; Sethares, William A.; Klein, Andrew G. (2011-08-18). "11". Software Receiver Design. Cambridge University Press. ISBN 978-1139501453.   Also https://cnx.org/contents/QsVBJjB4@3.1:6R_ztzDY@4/Pulse-Shaping-and-Receive-Filtering
  22. ↑ Nuttall, Albert H. (Feb 1981). "Some Windows with Very Good Sidelobe Behavior". IEEE Transactions on Acoustics, Speech, and Signal Processing 29 (1): 84–91. doi:10.1109/TASSP.1981.1163506. https://zenodo.org/record/1280930.  Extends Harris' paper, covering all the window functions known at the time, along with key metric comparisons.
  23. ↑ Weisstein, Eric W.. "Blackman Function" (in en). http://mathworld.wolfram.com/BlackmanFunction.html. 
  24. ↑ "Characteristics of Different Smoothing Windows - NI LabVIEW 8.6 Help". http://zone.ni.com/reference/en-XX/help/371361E-01/lvanlsconcepts/char_smoothing_windows/#Exact_Blackman. 
  25. ↑ Blackman, R.B.; Tukey, J.W. (1959-01-01). The Measurement of Power Spectra from the Point of View of Communications Engineering. Dover Publications. p. 99. ISBN 9780486605074. https://smile.amazon.com/Measurement-Power-Spectra-Communications-Engineering/dp/B0006AW1C4. 
  26. ↑ "Blackman-Harris Window Family". https://ccrma.stanford.edu/~jos/sasp/Blackman_Harris_Window_Family.html. 
  27. ↑ "Three-Term Blackman-Harris Window". https://ccrma.stanford.edu/~jos/sasp/Three_Term_Blackman_Harris_Window.html. 
  28. ↑ 28.0 28.1 Smith, Steven W. (2011). The Scientist and Engineer's Guide to Digital Signal Processing. San Diego, California, USA: California Technical Publishing. http://www.dspguide.com/ch9/1.htm. Retrieved 2013-02-14. 
  29. ↑ Rife, David C.; Vincent, G.A. (1970), "Use of the discrete Fourier transform in the measurement of frequencies and levels of tones", Bell Syst. Tech. J. 49 (2): 197–228, doi:10.1002/j.1538-7305.1970.tb01766.x 
  30. ↑ 30.0 30.1 Andria, Gregorio; Savino, Mario; Trotta, Amerigo (1989), "Windows and interpolation algorithms to improve electrical measurement accuracy", IEEE Transactions on Instrumentation and Measurement 38 (4): 856–863, doi:10.1109/19.31004 
  31. ↑ Schoukens, Joannes; Pintelon, Rik; Van Hamme, Hugo (1992), "The interpolated fast Fourier transform: a comparative study", IEEE Transactions on Instrumentation and Measurement 41 (2): 226–232, doi:10.1109/19.137352 
  32. ↑ 32.0 32.1 "Matlab for the Gaussian Window". https://ccrma.stanford.edu/~jos/sasp/Matlab_Gaussian_Window.html. "Note that, on a dB scale, Gaussians are quadratic. This means that parabolic interpolation of a sampled Gaussian transform is exact. ... quadratic interpolation of spectral peaks may be more accurate on a log-magnitude scale (e.g., dB) than on a linear magnitude scale" 
  33. ↑ "Gaussian Window and Transform". https://ccrma.stanford.edu/~jos/sasp/Gaussian_Window_Transform.html. 
  34. ↑ "Quadratic Interpolation of Spectral Peaks". https://ccrma.stanford.edu/~jos/sasp/Quadratic_Interpolation_Spectral_Peaks.html. 
  35. ↑ 35.0 35.1 35.2 Starosielec, S.; Hägele, D. (2014). "Discrete-time windows with minimal RMS bandwidth for given RMS temporal width". Signal Processing 102: 240–246. doi:10.1016/j.sigpro.2014.03.033. 
  36. ↑ Chakraborty, Debejyo; Kovvali, Narayan (2013). "Generalized normal window for digital signal processing". 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. pp. 6083–6087. doi:10.1109/ICASSP.2013.6638833. ISBN 978-1-4799-0356-6. 
  37. ↑ Diethorn, E.J. (1994). "The generalized exponential time-frequency distribution". IEEE Transactions on Signal Processing 42 (5): 1028–1037. doi:10.1109/78.295214. Bibcode: 1994ITSP...42.1028D. 
  38. ↑ Bloomfield, P. (2000). Fourier Analysis of Time Series: An Introduction. New York: Wiley-Interscience. 
  39. ↑ Tu, Loring W. (2008). "Bump Functions and Partitions of Unity". An Introduction to Manifolds. Universitext. New York: Springer. pp. 127–134. doi:10.1007/978-0-387-48101-2_13. ISBN 978-0-387-48098-5. 
  40. ↑ McKechan, D.J.A.; Robinson, C.; Sathyaprakash, B.S. (21 April 2010). "A tapering window for time-domain templates and simulated signals in the detection of gravitational waves from coalescing compact binaries". Classical and Quantum Gravity 27 (8): 084020. doi:10.1088/0264-9381/27/8/084020. Bibcode: 2010CQGra..27h4020M. 
  41. ↑ "Slepian or DPSS Window". https://ccrma.stanford.edu/~jos/sasp/Slepian_DPSS_Window.html. 
  42. ↑ 42.0 42.1 Smith, J.O. (2011). "Kaiser and DPSS Windows Compared". https://ccrma.stanford.edu/~jos/sasp/Kaiser_DPSS_Windows_Compared.html. 
  43. ↑ Kaiser, James F.; Kuo, Franklin F. (1966). System Analysis by Digital Computer. John Wiley and Sons. pp. 232–235. "This family of window functions was "discovered" by Kaiser in 1962 following a discussion with B. F. Logan of the Bell Telephone Laboratories. ... Another valuable property of this family ... is that they also approximate closely the prolate spheroidal wave functions of order zero." 
  44. ↑ Kaiser, James F. (Nov 1964). "A family of window functions having nearly ideal properties". Unpublished Memorandum. 
  45. ↑ Rabiner, Lawrence R.; Gold, Bernard (1975). "3.11". Theory and application of digital signal processing. Englewood Cliffs, N.J.: Prentice-Hall. p. 94. ISBN 0-13-914101-4. https://archive.org/details/theoryapplicatio00rabi/page/94. 
  46. ↑ Crochiere, R.E.; Rabiner, L.R. (1983). "4.3.1". Multirate Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall. p. 144. ISBN 0136051626. https://kupdf.net/download/multirate-digital-signal-processing-crochiere-rabiner_58a7065b6454a7e80bb1e993_pdf. 
  47. ↑ Lin, Yuan-Pei; Vaidyanathan, P.P. (June 1998). "A Kaiser Window Approach for the Design of Prototype Filters of Cosine Modulated Filterbanks". IEEE Signal Processing Letters 5 (6): 132–134. doi:10.1109/97.681427. Bibcode: 1998ISPL....5..132L. http://authors.library.caltech.edu/6891/1/LINieeespl98.pdf. Retrieved 2017-03-16. 
  48. ↑ Smith, J.O. (2011). "Kaiser Window". https://ccrma.stanford.edu/~jos/sasp/Kaiser_Window.html. "Sometimes the Kaiser window is parametrized by α, where β = πα." 
  49. ↑ "Kaiser Window, R2020a". Mathworks. https://www.mathworks.com/help/signal/ref/kaiser.html. 
  50. ↑ Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999). "7.2". Discrete-time signal processing (2nd ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 465–478. ISBN 0-13-754920-2. https://archive.org/details/discretetimesign00alan.   url=https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf
  51. ↑ "Kaiser Window". https://www.dsprelated.com/freebooks/sasp/Kaiser_Window.html. "The following Matlab comparison of the DPSS and Kaiser windows illustrates the interpretation of α as the bin number of the edge of the critically sampled window main lobe." 
  52. ↑ Kaiser, James F.; Schafer, Ronald W. (1980). "On the use of the I0-sinh window for spectrum analysis". IEEE Transactions on Acoustics, Speech, and Signal Processing 28: 105–107. doi:10.1109/TASSP.1980.1163349. 
  53. ↑ 53.0 53.1 53.2 "Dolph-Chebyshev Window". https://ccrma.stanford.edu/~jos/sasp/Dolph_Chebyshev_Window.html. 
  54. ↑ "Dolph-Chebyshev Window Definition". https://ccrma.stanford.edu/~jos/sasp/Dolph_Chebyshev_Window_Definition.html. 
  55. ↑ 55.0 55.1 55.2 Kabal, Peter (2009). "Time Windows for Linear Prediction of Speech". Technical Report, Dept. Elec. & Comp. Eng., McGill University (2a): 31. http://www-mmsp.ece.mcgill.ca/Documents/Reports/2009/KabalR2009b.pdf. Retrieved 2 February 2014. 
  56. ↑ Streit, Roy (1984). "A two-parameter family of weights for nonrecursive digital filters and antennas". Transactions of ASSP 32: 108–118. doi:10.1109/tassp.1984.1164275. https://zenodo.org/record/1280988. 
  57. ↑ 57.0 57.1 57.2 57.3 Deczky, Andrew (2001). "Unispherical Windows". ISCAS 2001. The 2001 IEEE International Symposium on Circuits and Systems (Cat. No.01CH37196). 2. pp. 85–88. doi:10.1109/iscas.2001.921012. ISBN 978-0-7803-6685-5. 
  58. ↑ Bergen, S.W.A.; Antoniou, A. (2004). "Design of Ultraspherical Window Functions with Prescribed Spectral Characteristics". EURASIP Journal on Applied Signal Processing 2004 (13): 2053–2065. doi:10.1155/S1110865704403114. Bibcode: 2004EJASP2004...63B. 
  59. ↑ Bergen, Stuart W. A. (2005). "Design of the Ultraspherical Window Function and Its Applications". https://dspace.library.uvic.ca/bitstream/handle/1828/769/bergen_2005.pdf?sequence=1.  Dissertation, University of Viktoria.
  60. ↑ Smith, Julius O. III (2011-04-23). "Poisson Window". https://ccrma.stanford.edu/~jos/sasp/Poisson_Window.html. 
  61. ↑ Gade, Svend; Herlufsen, Henrik (1987). "Technical Review No 3-1987: Windows to FFT analysis (Part I)". Brüel & Kjær. http://www.bksv.com/doc/Bv0031.pdf. 
  62. ↑ Berry, C.P.L.; Gair, J.R. (12 December 2012). "Observing the Galaxy's massive black hole with gravitational wave bursts". Monthly Notices of the Royal Astronomical Society 429 (1): 589–612. doi:10.1093/mnras/sts360. Bibcode: 2013MNRAS.429..589B. 
  63. ↑ "Hann-Poisson Window". https://ccrma.stanford.edu/~jos/sasp/Hann_Poisson_Window.html. 
  64. ↑ Justo, J. F.; Beccaro, W. (2020-10-26). "Generalized Adaptive Polynomial Window Function". IEEE Access 8: 187584–187589. doi:10.1109/ACCESS.2020.3030903. 
  65. ↑ Wesley Beccaro (2020-10-31), Generalized Adaptive Polynomial Window Function, https://www.mathworks.com/matlabcentral/fileexchange/81658-gap-generalized-adaptive-polynomial-window-function?s_tid=LandingPageTabfx&s_tid=mwa_osa_a, retrieved 2020-11-02 
  66. ↑ "Generalized Adaptive Polynomial Window Function". https://www.mathworks.com/matlabcentral/fileexchange/81658-gap-generalized-adaptive-polynomial-window-function. 




Retrieved from "https://handwiki.org/wiki/index.php?title=List_of_window_functions&oldid=2643279"