Mahalanobis distance

From HandWiki
Short description: Statistical distance measure

The Mahalanobis distance is a measure of the distance between a point [math]\displaystyle{ P }[/math] and a distribution [math]\displaystyle{ D }[/math], introduced by P. C. Mahalanobis in 1936.[1] Mahalanobis's definition was prompted by the problem of identifying the similarities of skulls based on measurements in 1927.[2]

It is a multivariate generalization of the square of the standard score [math]\displaystyle{ z=(x- \mu)/\sigma }[/math]: how many standard deviations away [math]\displaystyle{ P }[/math] is from the mean of [math]\displaystyle{ D }[/math]. This distance is zero for [math]\displaystyle{ P }[/math] at the mean of [math]\displaystyle{ D }[/math] and grows as [math]\displaystyle{ P }[/math] moves away from the mean along each principal component axis. If each of these axes is re-scaled to have unit variance, then the Mahalanobis distance corresponds to standard Euclidean distance in the transformed space. The Mahalanobis distance is thus unitless, scale-invariant, and takes into account the correlations of the data set.

Definition

Given a probability distribution [math]\displaystyle{ Q }[/math] on [math]\displaystyle{ \R^N }[/math], with mean [math]\displaystyle{ \vec{\mu} = (\mu_1, \mu_2, \mu_3, \dots , \mu_N)^\mathsf{T} }[/math] and positive-definite covariance matrix [math]\displaystyle{ S }[/math], the Mahalanobis distance of a point [math]\displaystyle{ \vec{x} = (x_1, x_2, x_3, \dots, x_N )^\mathsf{T} }[/math] from [math]\displaystyle{ Q }[/math] is[3][math]\displaystyle{ d_M(\vec{x}, Q) = \sqrt{(\vec{x} - \vec{\mu})^\mathsf{T} S^{-1} (\vec{x} - \vec{\mu})}. }[/math]Given two points [math]\displaystyle{ \vec{x} }[/math] and [math]\displaystyle{ \vec{y} }[/math] in [math]\displaystyle{ \R^N }[/math], the Mahalanobis distance between them with respect to [math]\displaystyle{ Q }[/math] is[math]\displaystyle{ d_M(\vec{x} ,\vec{y}; Q) = \sqrt{(\vec{x} - \vec{y})^\mathsf{T} S^{-1} (\vec{x} - \vec{y})}. }[/math]which means that [math]\displaystyle{ d_M(\vec{x}, Q) = d_M(\vec{x},\vec{\mu}; Q) }[/math].

Since [math]\displaystyle{ S }[/math] is positive-definite, so is [math]\displaystyle{ S^{-1} }[/math], thus the square roots are always defined.

We can find useful decompositions of the squared Mahalanobis distance that help to explain some reasons for the outlyingness of multivariate observations and also provide a graphical tool for identifying outliers.[4]

By the spectral theorem, [math]\displaystyle{ S^{-1} }[/math] can be decomposed as [math]\displaystyle{ S^{-1} = W^T W }[/math] for some real [math]\displaystyle{ N\times N }[/math] matrix, which gives us the equivalent definition[math]\displaystyle{ d_M(\vec{x}, \vec{y}; Q) = \|W(\vec{x} - \vec{y})\| }[/math]where [math]\displaystyle{ \|\cdot\| }[/math] is the Euclidean norm. That is, the Mahalanobis distance is the Euclidean distance after a whitening transformation.

The existence of [math]\displaystyle{ W }[/math] is guaranteed by the spectral theorem, but it is not unique. Different choices have different theoretical and practical advantages.[5]

In practice, the distribution [math]\displaystyle{ Q }[/math] is usually the sample distribution from a set of IID samples from an underlying unknown distribution, so [math]\displaystyle{ \mu }[/math] is the sample mean, and [math]\displaystyle{ S }[/math] is the covariance matrix of the samples.

When the affine span of the samples is not the entire [math]\displaystyle{ \R^N }[/math], the covariance matrix would not be positive-definite, which means the above definition would not work. However, in general, the Mahalanobis distance is preserved under any full-rank affine transformation of the affine span of the samples. So in case the affine span is not the entire [math]\displaystyle{ \R^N }[/math], the samples can be first orthogonally projected to [math]\displaystyle{ \R^n }[/math], where [math]\displaystyle{ n }[/math] is the dimension of the affine span of the samples, then the Mahalanobis distance can be computed as usual.

Intuitive explanation

Consider the problem of estimating the probability that a test point in N-dimensional Euclidean space belongs to a set, where we are given sample points that definitely belong to that set. Our first step would be to find the centroid or center of mass of the sample points. Intuitively, the closer the point in question is to this center of mass, the more likely it is to belong to the set.

However, we also need to know if the set is spread out over a large range or a small range, so that we can decide whether a given distance from the center is noteworthy or not. The simplistic approach is to estimate the standard deviation of the distances of the sample points from the center of mass. If the distance between the test point and the center of mass is less than one standard deviation, then we might conclude that it is highly probable that the test point belongs to the set. The further away it is, the more likely that the test point should not be classified as belonging to the set.

This intuitive approach can be made quantitative by defining the normalized distance between the test point and the set to be [math]\displaystyle{ \frac{\lVert x - \mu\rVert_2}{\sigma} }[/math], which reads: [math]\displaystyle{ \frac{\text{testpoint} - \text{sample mean}}{\text{standard deviation}} }[/math]. By plugging this into the normal distribution, we can derive the probability of the test point belonging to the set.

The drawback of the above approach was that we assumed that the sample points are distributed about the center of mass in a spherical manner. Were the distribution to be decidedly non-spherical, for instance ellipsoidal, then we would expect the probability of the test point belonging to the set to depend not only on the distance from the center of mass, but also on the direction. In those directions where the ellipsoid has a short axis the test point must be closer, while in those where the axis is long the test point can be further away from the center.

Putting this on a mathematical basis, the ellipsoid that best represents the set's probability distribution can be estimated by building the covariance matrix of the samples. The Mahalanobis distance is the distance of the test point from the center of mass divided by the width of the ellipsoid in the direction of the test point.

Normal distributions

For a normal distribution in any number of dimensions, the probability density of an observation [math]\displaystyle{ \vec{x} }[/math] is uniquely determined by the Mahalanobis distance [math]\displaystyle{ d }[/math]:

[math]\displaystyle{ \begin{align} \Pr[\vec x] \,d\vec x & = \frac 1 {\sqrt{\det(2\pi \mathbf{S})}} \exp \left(-\frac{(\vec x - \vec \mu)^\mathsf{T} \mathbf{S}^{-1} (\vec x - \vec \mu)} 2 \right) \,d\vec{x} \\[6pt] & = \frac{1}{\sqrt{\det(2\pi \mathbf{S})}} \exp\left( -\frac{d^2} 2 \right) \,d\vec x. \end{align} }[/math]

Specifically, [math]\displaystyle{ d^2 }[/math] follows the chi-squared distribution with [math]\displaystyle{ n }[/math] degrees of freedom, where [math]\displaystyle{ n }[/math] is the number of dimensions of the normal distribution. If the number of dimensions is 2, for example, the probability of a particular calculated [math]\displaystyle{ d }[/math] being less than some threshold [math]\displaystyle{ t }[/math] is [math]\displaystyle{ 1 - e^{-t^2/2} }[/math]. To determine a threshold to achieve a particular probability, [math]\displaystyle{ p }[/math], use [math]\displaystyle{ t = \sqrt{-2\ln(1 - p)} }[/math], for 2 dimensions. For number of dimensions other than 2, the cumulative chi-squared distribution should be consulted.

In a normal distribution, the region where the Mahalanobis distance is less than one (i.e. the region inside the ellipsoid at distance one) is exactly the region where the probability distribution is concave.

The Mahalanobis distance is proportional, for a normal distribution, to the square root of the negative log-likelihood (after adding a constant so the minimum is at zero).

Other forms of multivariate location and scatter

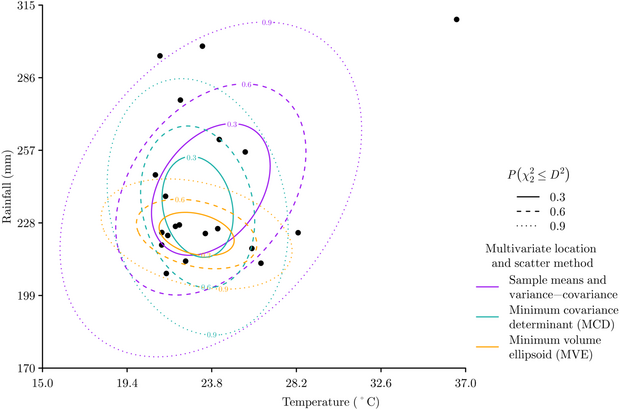
Hypothetical two-dimensional example of Mahalanobis distance with three different methods of defining the multivariate location and scatter of the data.

The sample mean and covariance matrix can be quite sensitive to outliers, therefore other approaches for calculating the multivariate location and scatter of data are also commonly used when calculating the Mahalanobis distance. The Minimum Covariance Determinant approach estimates multivariate location and scatter from a subset numbering [math]\displaystyle{ h }[/math] data points that has the smallest variance-covariance matrix determinant.[6] The Minimum Volume Ellipsoid approach is similar to the Minimum Covariance Determinant approach in that it works with a subset of size [math]\displaystyle{ h }[/math] data points, but the Minimum Volume Ellipsoid estimates multivariate location and scatter from the ellipsoid of minimal volume that encapsulates the [math]\displaystyle{ h }[/math] data points.[7] Each method varies in its definition of the distribution of the data, and therefore produces different Mahalanobis distances. The Minimum Covariance Determinant and Minimum Volume Ellipsoid approaches are more robust to samples that contain outliers, while the sample mean and covariance matrix tends to be more reliable with small and biased data sets.[8]

Relationship to normal random variables

In general, given a normal (Gaussian) random variable [math]\displaystyle{ X }[/math] with variance [math]\displaystyle{ S=1 }[/math] and mean [math]\displaystyle{ \mu = 0 }[/math], any other normal random variable [math]\displaystyle{ R }[/math] (with mean [math]\displaystyle{ \mu_1 }[/math] and variance [math]\displaystyle{ S_1 }[/math]) can be defined in terms of [math]\displaystyle{ X }[/math] by the equation [math]\displaystyle{ R = \mu_1 + \sqrt{S_1}X. }[/math] Conversely, to recover a normalized random variable from any normal random variable, one can typically solve for [math]\displaystyle{ X = (R - \mu_1)/\sqrt{S_1} }[/math]. If we square both sides, and take the square-root, we will get an equation for a metric that looks a lot like the Mahalanobis distance:

[math]\displaystyle{ D = \sqrt{X^2} = \sqrt{(R - \mu_1)^2/S_1} = \sqrt{(R - \mu_1) S_1^{-1} (R - \mu_1) }. }[/math]

The resulting magnitude is always non-negative and varies with the distance of the data from the mean, attributes that are convenient when trying to define a model for the data.

Relationship to leverage

Mahalanobis distance is closely related to the leverage statistic, [math]\displaystyle{ h }[/math], but has a different scale:

[math]\displaystyle{ D^2 = (N - 1) \left(h - \tfrac 1 N \right). }[/math]

Applications

Mahalanobis distance is widely used in cluster analysis and classification techniques. It is closely related to Hotelling's T-square distribution used for multivariate statistical testing and Fisher's Linear Discriminant Analysis that is used for supervised classification.[9]

In order to use the Mahalanobis distance to classify a test point as belonging to one of N classes, one first estimates the covariance matrix of each class, usually based on samples known to belong to each class. Then, given a test sample, one computes the Mahalanobis distance to each class, and classifies the test point as belonging to that class for which the Mahalanobis distance is minimal.

Mahalanobis distance and leverage are often used to detect outliers, especially in the development of linear regression models. A point that has a greater Mahalanobis distance from the rest of the sample population of points is said to have higher leverage since it has a greater influence on the slope or coefficients of the regression equation. Mahalanobis distance is also used to determine multivariate outliers. Regression techniques can be used to determine if a specific case within a sample population is an outlier via the combination of two or more variable scores. Even for normal distributions, a point can be a multivariate outlier even if it is not a univariate outlier for any variable (consider a probability density concentrated along the line [math]\displaystyle{ x_1 = x_2 }[/math], for example), making Mahalanobis distance a more sensitive measure than checking dimensions individually.

Mahalanobis distance has also been used in ecological niche modelling,[10][11] as the convex elliptical shape of the distances relates well to the concept of the fundamental niche.

Another example of usage is in finance, where Mahalanobis distance has been used to compute an indicator called the "turbulence index",[12] which is a statistical measure of financial markets abnormal behaviour. An implementation as a Web API of this indicator is available online.[13]

Software implementations

Many programming languages and statistical packages, such as R, Python, etc., include implementations of Mahalanobis distance.

Language/program Function Ref.
Julia mahalanobis(x, y, Q) [1]
MATLAB mahal(x, y) [2]
R mahalanobis(x, center, cov, inverted = FALSE, ...) [3]
SciPy (Python) mahalanobis(u, v, VI) [4]

See also

References

  1. ↑ Mahalanobis, Prasanta Chandra (1936). "On the generalised distance in statistics". Proceedings of the National Institute of Sciences of India 2 (1): 49–55. http://library.isical.ac.in:8080/xmlui/bitstream/handle/10263/6765/Vol02_1936_1_Art05-pcm.pdf. Retrieved 2016-09-27. 
  2. ↑ Mahalanobis, Prasanta Chandra (1927); Analysis of race mixture in Bengal, Journal and Proceedings of the Asiatic Society of Bengal, 23:301–333.
  3. ↑ De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D. L. (2000). "The Mahalanobis distance". Chemometrics and Intelligent Laboratory Systems 50 (1): 1–18. doi:10.1016/s0169-7439(99)00047-7. 
  4. ↑ Kim, M. G. (2000). "Multivariate outliers and decompositions of Mahalanobis distance". Communications in Statistics – Theory and Methods 29 (7): 1511–1526. doi:10.1080/03610920008832559. 
  5. ↑ Kessy, Agnan; Lewin, Alex; Strimmer, Korbinian (2018-10-02). "Optimal Whitening and Decorrelation". The American Statistician 72 (4): 309–314. doi:10.1080/00031305.2016.1277159. ISSN 0003-1305. https://doi.org/10.1080/00031305.2016.1277159. 
  6. ↑ Hubert, Mia; Debruyne, Michiel (2010). "Minimum covariance determinant" (in en). WIREs Computational Statistics 2 (1): 36–43. doi:10.1002/wics.61. ISSN 1939-5108. https://onlinelibrary.wiley.com/doi/10.1002/wics.61. 
  7. ↑ Van Aelst, Stefan; Rousseeuw, Peter (2009). "Minimum volume ellipsoid" (in en). Wiley Interdisciplinary Reviews: Computational Statistics 1 (1): 71–82. doi:10.1002/wics.19. ISSN 1939-5108. https://onlinelibrary.wiley.com/doi/10.1002/wics.19. 
  8. ↑ Etherington, Thomas R. (2021-05-11). "Mahalanobis distances for ecological niche modelling and outlier detection: implications of sample size, error, and bias for selecting and parameterising a multivariate location and scatter method" (in en). PeerJ 9: e11436. doi:10.7717/peerj.11436. ISSN 2167-8359. PMID 34026369. 
  9. ↑ McLachlan, Geoffrey (4 August 2004). Discriminant Analysis and Statistical Pattern Recognition. John Wiley & Sons. pp. 13–. ISBN 978-0-471-69115-0. https://books.google.com/books?id=O_qHDLaWpDUC&pg=PR13. 
  10. ↑ Etherington, Thomas R. (2019-04-02). "Mahalanobis distances and ecological niche modelling: correcting a chi-squared probability error" (in en). PeerJ 7: e6678. doi:10.7717/peerj.6678. ISSN 2167-8359. PMID 30972255. 
  11. ↑ Farber, Oren; Kadmon, Ronen (2003). "Assessment of alternative approaches for bioclimatic modeling with special emphasis on the Mahalanobis distance" (in en). Ecological Modelling 160 (1–2): 115–130. doi:10.1016/S0304-3800(02)00327-7. 
  12. ↑ Kritzman, M.; Li, Y. (2019-04-02). "Skulls, Financial Turbulence, and Risk Management" (in en). Financial Analysts Journal 66 (5): 30–41. doi:10.2469/faj.v66.n5.3. https://www.tandfonline.com/doi/abs/10.2469/faj.v66.n5.3. 
  13. ↑ "Portfolio Optimizer". https://portfoliooptimizer.io/. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Mahalanobis_distance&oldid=3359988"