Physics:Hexagonal crystal family
| Crystal system | Trigonal | Hexagonal | |
|---|---|---|---|
| Lattice system | 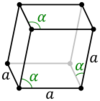 Rhombohedral |
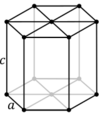 Hexagonal | |
| Example |  Dolomite (white) |
 α-Quartz |
 Beryl |
In crystallography, the hexagonal crystal family is one of the 6 crystal families, which includes two crystal systems (hexagonal and trigonal) and two lattice systems (hexagonal and rhombohedral). While commonly confused, the trigonal crystal system and the rhombohedral lattice system are not equivalent (see section crystal systems below).[1] In particular, there are crystals that have trigonal symmetry but belong to the hexagonal lattice (such as α-quartz).
The hexagonal crystal family consists of the 12 point groups such that at least one of their space groups has the hexagonal lattice as underlying lattice, and is the union of the hexagonal crystal system and the trigonal crystal system.[2] There are 52 space groups associated with it, which are exactly those whose Bravais lattice is either hexagonal or rhombohedral.
Lattice systems
The hexagonal crystal family consists of two lattice systems: hexagonal and rhombohedral. Each lattice system consists of one Bravais lattice.
| Bravais lattice | Hexagonal | Rhombohedral |
|---|---|---|
| Pearson symbol | hP | hR |
| Hexagonal unit cell |
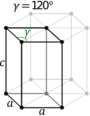
|
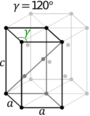
|
| Rhombohedral unit cell |
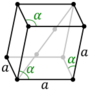
|
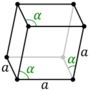
|
In the hexagonal family, the crystal is conventionally described by a right rhombic prism unit cell with two equal axes (a by a), an included angle of 120° (γ) and a height (c, which can be different from a) perpendicular to the two base axes.
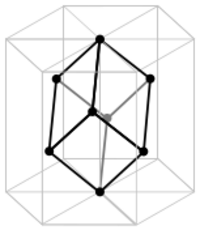
The hexagonal unit cell for the rhombohedral Bravais lattice is the R-centered cell, consisting of two additional lattice points which occupy one body diagonal of the unit cell. There are two ways to do this, which can be thought of as two notations which represent the same structure. In the usual so-called obverse setting, the additional lattice points are at coordinates (2⁄3, 1⁄3, 1⁄3) and (1⁄3, 2⁄3, 2⁄3), whereas in the alternative reverse setting they are at the coordinates (1⁄3,2⁄3,1⁄3) and (2⁄3,1⁄3,2⁄3).[3] In either case, there are 3 lattice points per unit cell in total and the lattice is non-primitive.
The Bravais lattices in the hexagonal crystal family can also be described by rhombohedral axes.[4] The unit cell is a rhombohedron (which gives the name for the rhombohedral lattice). This is a unit cell with parameters a = b = c; α = β = γ ≠ 90°.[5] In practice, the hexagonal description is more commonly used because it is easier to deal with a coordinate system with two 90° angles. However, the rhombohedral axes are often shown (for the rhombohedral lattice) in textbooks because this cell reveals the 3m symmetry of the crystal lattice.
The rhombohedral unit cell for the hexagonal Bravais lattice is the D-centered[1] cell, consisting of two additional lattice points which occupy one body diagonal of the unit cell with coordinates (1⁄3, 1⁄3, 1⁄3) and (2⁄3, 2⁄3, 2⁄3). However, such a description is rarely used.
Crystal systems
| Crystal system | Required symmetries of point group | Point groups | Space groups | Bravais lattices | Lattice system |
|---|---|---|---|---|---|
| Trigonal | 1 threefold axis of rotation | 5 | 7 | 1 | Rhombohedral |
| 18 | 1 | Hexagonal | |||
| Hexagonal | 1 sixfold axis of rotation | 7 | 27 |
The hexagonal crystal family consists of two crystal systems: trigonal and hexagonal. A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system (see table in Crystal system).
The trigonal crystal system consists of the 5 point groups that have a single three-fold rotation axis, which includes space groups 143 to 167. These 5 point groups have 7 corresponding space groups (denoted by R) assigned to the rhombohedral lattice system and 18 corresponding space groups (denoted by P) assigned to the hexagonal lattice system. Hence, the trigonal crystal system is the only crystal system whose point groups have more than one lattice system associated with their space groups.
The hexagonal crystal system consists of the 7 point groups that have a single six-fold rotation axis. These 7 point groups have 27 space groups (168 to 194), all of which are assigned to the hexagonal lattice system.
Trigonal crystal system
The 5 point groups in this crystal system are listed below, with their international number and notation, their space groups in name and example crystals.[6][7][8]
| Space group no. | Point group | Type | Examples | Space groups | |||||
|---|---|---|---|---|---|---|---|---|---|
| Name[1] | Intl | Schoen. | Orb. | Cox. | Hexagonal | Rhombohedral | |||
| 143–146 | Trigonal pyramidal | 3 | C3 | 33 | [3]+ | enantiomorphic polar | carlinite, jarosite | P3, P31, P32 | R3 |
| 147–148 | Rhombohedral | 3 | C3i (S6) | 3× | [2+,6+] | centrosymmetric | dolomite, ilmenite | P3 | R3 |
| 149–155 | Trigonal trapezohedral | 32 | D3 | 223 | [2,3]+ | enantiomorphic | abhurite, alpha-quartz (152, 154), cinnabar | P312, P321, P3112, P3121, P3212, P3221 | R32 |
| 156–161 | Ditrigonal pyramidal | 3m | C3v | *33 | [3] | polar | schorl, cerite, tourmaline, alunite, lithium tantalate | P3m1, P31m, P3c1, P31c | R3m, R3c |
| 162–167 | Ditrigonal scalenohedral | 3m | D3d | 2*3 | [2+,6] | centrosymmetric | antimony, hematite, corundum, calcite, bismuth | P31m, P31c, P3m1, P3c1 | R3m, R3c |
Hexagonal crystal system
The 7 point groups (crystal classes) in this crystal system are listed below, followed by their representations in Hermann–Mauguin or international notation and Schoenflies notation, and mineral examples, if they exist.[2][9]
| Space group no. | Point group | Type | Examples | Space groups | ||||
|---|---|---|---|---|---|---|---|---|
| Name[1] | Intl | Schoen. | Orb. | Cox. | ||||
| 168–173 | Hexagonal pyramidal | 6 | C6 | 66 | [6]+ | enantiomorphic polar | nepheline, cancrinite | P6, P61, P65, P62, P64, P63 |
| 174 | Trigonal dipyramidal | 6 | C3h | 3* | [2,3+] | laurelite and boric acid | P6 | |
| 175–176 | Hexagonal dipyramidal | 6/m | C6h | 6* | [2,6+] | centrosymmetric | apatite, vanadinite | P6/m, P63/m |
| 177–182 | Hexagonal trapezohedral | 622 | D6 | 226 | [2,6]+ | enantiomorphic | kalsilite and high quartz | P622, P6122, P6522, P6222, P6422, P6322 |
| 183–186 | Dihexagonal pyramidal | 6mm | C6v | *66 | [6] | polar | greenockite, wurtzite[10] | P6mm, P6cc, P63cm, P63mc |
| 187–190 | Ditrigonal dipyramidal | 6m2 | D3h | *223 | [2,3] | benitoite | P6m2, P6c2, P62m, P62c | |
| 191–194 | Dihexagonal dipyramidal | 6/mmm | D6h | *226 | [2,6] | centrosymmetric | beryl | P6/mmm, P6/mcc, P63/mcm, P63/mmc |
The unit cell volume is given by a2c•sin(60°)
Hexagonal close packed
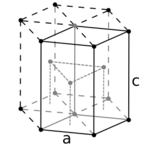
Hexagonal close packed (hcp) is one of the two simple types of atomic packing with the highest density, the other being the face-centered cubic (fcc). However, unlike the fcc, it is not a Bravais lattice, as there are two nonequivalent sets of lattice points. Instead, it can be constructed from the hexagonal Bravais lattice by using a two-atom motif (the additional atom at about (2⁄3, 1⁄3, 1⁄2)) associated with each lattice point.[11]
Multi-element structures
Compounds that consist of more than one element (e.g. binary compounds) often have crystal structures based on the hexagonal crystal family. Some of the more common ones are listed here. These structures can be viewed as two or more interpenetrating sublattices where each sublattice occupies the interstitial sites of the others.
Wurtzite structure
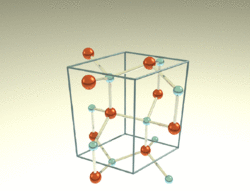
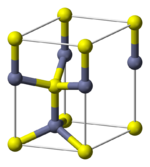
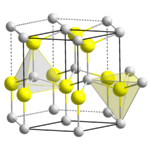
The wurtzite crystal structure is referred to by the Strukturbericht designation B4 and the Pearson symbol hP4. The corresponding space group is No. 186 (in International Union of Crystallography classification) or P63mc (in Hermann–Mauguin notation). The Hermann-Mauguin symbols in P63mc can be read as follows:[13]
- 63.. : a six fold screw rotation around the c-axis
- .m. : a mirror plane with normal {100}
- ..c : glide plane in the c-directions with normal {120}.
Among the compounds that can take the wurtzite structure are wurtzite itself (ZnS with up to 8% iron instead of zinc), silver iodide (AgI), zinc oxide (ZnO), cadmium sulfide (CdS), cadmium selenide (CdSe), silicon carbide (α-SiC), gallium nitride (GaN), aluminium nitride (AlN), boron nitride (w-BN) and other semiconductors.[14] In most of these compounds, wurtzite is not the favored form of the bulk crystal, but the structure can be favored in some nanocrystal forms of the material.
In materials with more than one crystal structure, the prefix "w-" is sometimes added to the empirical formula to denote the wurtzite crystal structure, as in w-BN.
Each of the two individual atom types forms a sublattice which is hexagonal close-packed (HCP-type). When viewed all together, the atomic positions are the same as in lonsdaleite (hexagonal diamond). Each atom is tetrahedrally coordinated. The structure can also be described as an HCP lattice of zinc with sulfur atoms occupying half of the tetrahedral voids or vice versa.
The wurtzite structure is non-centrosymmetric (i.e., lacks inversion symmetry). Due to this, wurtzite crystals can (and generally do) have properties such as piezoelectricity and pyroelectricity, which centrosymmetric crystals lack.[citation needed]
Nickel arsenide structure
The nickel arsenide structure consists of two interpenetrating sublattices: a primitive hexagonal nickel sublattice and a hexagonal close-packed arsenic sublattice. Each nickel atom is octahedrally coordinated to six arsenic atoms, while each arsenic atom is trigonal prismatically coordinated to six nickel atoms.[15] The structure can also be described as an HCP lattice of arsenic with nickel occupying each octahedral void.
Compounds adopting the NiAs structure are generally the chalcogenides, arsenides, antimonides and bismuthides of transition metals. [citation needed]
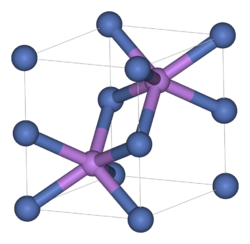
The following are the members of the nickeline group:[16]
- Achavalite: FeSe
- Breithauptite: NiSb
- Freboldite: CoSe
- Kotulskite: Pd(Te,Bi)
- Langistite: (Co,Ni)As
- Nickeline: NiAs
- Sobolevskite: Pd(Bi,Te)
- Sudburyite: (Pd,Ni)Sb
In two dimensions
There is only one hexagonal Bravais lattice in two dimensions: the hexagonal lattice.
| Bravais lattice | Hexagonal |
|---|---|
| Pearson symbol | hp |
| Unit cell | 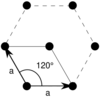
|
See also
References
- ↑ 1.0 1.1 1.2 1.3 Hahn, Theo, ed (2005). International tables for crystallography (5th ed.). Dordrecht, Netherlands: Published for the International Union of Crystallography by Springer. ISBN 978-0-7923-6590-7.
- ↑ 2.0 2.1 Dana, James Dwight; Hurlbut, Cornelius Searle (1959). Dana's Manual of Mineralogy (17th ed.). New York: Chapman Hall. pp. 78–89. https://books.google.com/books?id=e7MSMwEACAAJ.
- ↑ Edward Prince (2004). Mathematical Techniques in Crystallography and Materials Science. Springer Science & Business Media. p. 41.
- ↑ "Medium-Resolution Space Group Diagrams and Tables". http://img.chem.ucl.ac.uk/sgp/medium/sgp.htm.
- ↑ Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics (1st ed.). p. 119. ISBN 0-03-083993-9. https://archive.org/details/solidstatephysic00ashc/page/119.
- ↑ Pough, Frederick H.; Peterson, Roger Tory (1998). A Field Guide to Rocks and Minerals. Houghton Mifflin Harcourt. p. 62. ISBN 0-395-91096-X. https://books.google.com/books?id=co07Qn9HzP0C&pg=PA62.
- ↑ Hurlbut, Cornelius S.; Klein, Cornelis (1985). Manual of Mineralogy (20th ed.). pp. 78–89. ISBN 0-471-80580-7. https://archive.org/details/manualofmineralo00klei/page/78.
- ↑ "Crystallography and Minerals Arranged by Crystal Form". http://webmineral.com/crystall.shtml.
- ↑ "Crystallography". Webmineral.com. http://webmineral.com/crystall.shtml.
- ↑ "Minerals in the Hexagonal crystal system, Dihexagonal Pyramidal class (6mm)". Mindat.org. http://www.mindat.org/system_search.php?g=18.
- ↑ Jaswon, Maurice Aaron (1965-01-01) (in en). An introduction to mathematical crystallography. American Elsevier Pub. Co.. https://books.google.com/books?id=lTRRAAAAMAAJ.
- ↑ De Graef, Marc; McHenry, Michael E. (2012). Structure of Materials; An introduction to Crystallography, Diffraction and Symmetry. Cambridge University Press. p. 16. http://som.web.cmu.edu/StructuresAppendix2.pdf.
- ↑ Hitchcock, Peter B (1988). International tables for crystallography volume A.. https://www.springer.com/series/6995.
- ↑ Togo, Atsushi; Chaput, Laurent; Tanaka, Isao (2015-03-20). "Distributions of phonon lifetimes in Brillouin zones". Physical Review B 91 (9): 094306. doi:10.1103/PhysRevB.91.094306. Bibcode: 2015PhRvB..91i4306T.
- ↑ Inorganic Chemistry by Duward Shriver and Peter Atkins, 3rd Edition, W.H. Freeman and Company, 1999, pp.47,48.
- ↑ http://www.mindat.org/min-2901.html Mindat.org
External links
 |
