Physics:Negative mass
In theoretical physics, negative mass is a hypothetical type of exotic matter whose mass is of opposite sign to the mass of normal matter, e.g. −1 kg.[1][2] Such matter would violate one or more energy conditions and exhibit strange properties such as the oppositely oriented acceleration for an applied force orientation. It is used in certain speculative hypothetical technologies, such as time travel to the past and future,[3] construction of traversable artificial wormholes, which may also allow for time travel, Krasnikov tubes, the Alcubierre drive, and potentially other types of faster-than-light warp drives. Currently, the closest known real representative of such exotic matter is a region of negative pressure density produced by the Casimir effect.
In cosmology
In December 2018, astrophysicist Jamie Farnes from the University of Oxford proposed a "dark fluid" theory, related, in part, to notions of gravitationally repulsive negative masses, presented earlier by Albert Einstein, that may help better understand, in a testable manner, the considerable amounts of unknown dark matter and dark energy in the cosmos.[4][5]
In general relativity
Negative mass is any region of space in which for some observers the mass density is measured to be negative. This may occur due to a region of space in which the sum of the three normal stress components (pressure on each of three axes) of the Einstein stress–energy tensor is larger in magnitude than the mass density. All of these are violations of one or another variant of the positive energy condition of Einstein's general theory of relativity; however, the positive energy condition is not a required condition for the mathematical consistency of the theory.
Inertial versus gravitational mass
In considering negative mass, it is important to consider which of these concepts of mass are negative. Ever since Newton first formulated his theory of gravity, there have been at least three conceptually distinct quantities called mass:
- inertial mass – the mass m that appears in Newton's second law of motion, F = m a
- "active" gravitational mass – the mass that produces a gravitational field that other masses respond to
- "passive" gravitational mass – the mass that responds to an external gravitational field by accelerating.
The law of conservation of momentum requires that active and passive gravitational mass be identical. Einstein's equivalence principle postulates that inertial mass must equal passive gravitational mass, and all experimental evidence to date has found these are, indeed, always the same.
In most analyses of negative mass, it is assumed that the equivalence principle and conservation of momentum continue to apply without using any matter in the process, and therefore all three forms of mass are still the same, leading to the study of "negative mass". But the equivalence principle is simply an observational fact, and is not necessarily valid. If such a distinction is made, a "negative mass" can be of three kinds: whether the inertial mass is negative, the gravitational mass, or both.
In his 4th-prize essay for the 1951 Gravity Research Foundation competition, Joaquin Mazdak Luttinger considered the possibility of negative mass and how it would behave under gravitational and other forces.[6]
In 1957, following Luttinger's idea, Hermann Bondi suggested in a paper in Reviews of Modern Physics that mass might be negative as well as positive.[7] He pointed out that this does not entail a logical contradiction, as long as all three forms of mass are negative, but that the assumption of negative mass involves some counter-intuitive form of motion. For example, an object with negative inertial mass would be expected to accelerate in the opposite direction to that in which it was pushed (non-gravitationally).
There have been several other analyses of negative mass, such as the studies conducted by R. M. Price,[8] though none addressed the question of what kind of energy and momentum would be necessary to describe non-singular negative mass. Indeed, the Schwarzschild solution for negative mass parameter has a naked singularity at a fixed spatial position. The question that immediately comes up is, would it not be possible to smooth out the singularity with some kind of negative mass density. The answer is yes, but not with energy and momentum that satisfies the dominant energy condition. This is because if the energy and momentum satisfies the dominant energy condition within a spacetime that is asymptotically flat, which would be the case of smoothing out the singular negative mass Schwarzschild solution, then it must satisfy the positive energy theorem, i.e. its ADM mass must be positive, which is of course not the case.[9][10] However, it was noticed by Belletête and Paranjape that since the positive energy theorem does not apply to asymptotic de Sitter spacetime, it would actually be possible to smooth out, with energy–momentum that does satisfy the dominant energy condition, the singularity of the corresponding exact solution of negative mass Schwarzschild–de Sitter, which is the singular, exact solution of Einstein's equations with cosmological constant.[11] In a subsequent article, Mbarek and Paranjape showed that it is in fact possible to obtain the required deformation through the introduction of the energy–momentum of a perfect fluid.[12]
Runaway motion
Although no particles are known to have negative mass, physicists (primarily Hermann Bondi in 1957,[7] William B. Bonnor in 1964 and 1989,[13][14] then Robert L. Forward[15]) have been able to describe some of the anticipated properties such particles may have. Assuming that all three concepts of mass are equivalent according to the equivalence principle, the gravitational interactions between masses of arbitrary sign can be explored, based on the Newtonian approximation of the Einstein field equations. The interaction laws are then:
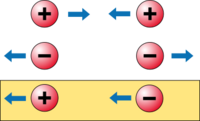
- Positive mass attracts both other positive masses and negative masses.
- Negative mass repels both other negative masses and positive masses.
For two positive masses, nothing changes and there is a gravitational pull on each other causing an attraction. Two negative masses would repel because of their negative inertial masses. For different signs however, there is a push that repels the positive mass from the negative mass, and a pull that attracts the negative mass towards the positive one at the same time.
Hence Bondi pointed out that two objects of equal and opposite mass would produce a constant acceleration of the system towards the positive-mass object,[7] an effect called "runaway motion" by Bonnor who disregarded its physical existence, stating:
| “ | I regard the runaway (or self-accelerating) motion […] so preposterous that I prefer to rule it out by supposing that inertial mass is all positive or all negative. | ” |
| — William B. Bonnor, in Negative mass in general relativity.[14] | ||
Such a couple of objects would accelerate without limit (except a relativistic one); however, the total mass, momentum and energy of the system would remain zero. This behavior is completely inconsistent with a common-sense approach and the expected behavior of "normal" matter. Thomas Gold even hinted that the runaway linear motion could be used in a perpetual motion machine if converted to circular motion:
| “ | What happens if one attaches a negative and positive mass pair to the rim of a wheel? This is incompatible with general relativity, for the device gets more massive. | ” |
| — Thomas Gold, in Negative mass in general relativity.[16] | ||
But Forward showed that the phenomenon is mathematically consistent and introduces no violation of conservation laws.[15] If the masses are equal in magnitude but opposite in sign, then the momentum of the system remains zero if they both travel together and accelerate together, no matter what their speed:
And equivalently for the kinetic energy:
However, this is perhaps not exactly valid if the energy in the gravitational field is taken into account.
Forward extended Bondi's analysis to additional cases, and showed that even if the two masses m(−) and m(+) are not the same, the conservation laws remain unbroken. This is true even when relativistic effects are considered, so long as inertial mass, not rest mass, is equal to gravitational mass.
This behaviour can produce bizarre results: for instance, a gas containing a mixture of positive and negative matter particles will have the positive matter portion increase in temperature without bound.[citation needed] However, the negative matter portion gains negative temperature at the same rate, again balancing out. Geoffrey A. Landis pointed out other implications of Forward's analysis,[17] including noting that although negative mass particles would repel each other gravitationally, the electrostatic force would be attractive for like charges and repulsive for opposite charges.
Forward used the properties of negative-mass matter to create the concept of diametric drive, a design for spacecraft propulsion using negative mass that requires no energy input and no reaction mass to achieve arbitrarily high acceleration.
Forward also coined a term, "nullification", to describe what happens when ordinary matter and negative matter meet: they are expected to be able to cancel out or nullify each other's existence. An interaction between equal quantities of positive mass matter (hence of positive energy E = mc2) and negative mass matter (of negative energy −E = −mc2) would release no energy, but because the only configuration of such particles that has zero momentum (both particles moving with the same velocity in the same direction) does not produce a collision, such interactions would leave a surplus of momentum.
Arrow of time and energy inversion
In general relativity, the universe is described as a Riemannian manifold associated to a metric tensor solution of Einstein's field equations. In such a framework, the runaway motion forbids the existence of negative matter.[7][14]
Some bimetric theories of the universe propose that two parallel universes with an opposite arrow of time may exist instead of one, linked together by the Big Bang and interacting only through gravitation.[18][19] The universe is then described as a manifold associated to two Riemannian metrics (one with positive mass matter and the other with negative mass matter). According to group theory, the matter of the conjugated metric would appear to the matter of the other metric as having opposite mass and arrow of time (though its proper time would remain positive). The coupled metrics have their own geodesics and are solutions of two coupled field equations.[20]
The negative matter of the coupled metric, interacting with the matter of the other metric via gravity, could be an alternative candidate for the explanation of dark matter, dark energy, cosmic inflation and an accelerating universe.[20]
Gravitational interaction of antimatter
The gravitational interaction of antimatter with matter has been observed by physicists.[21] As was the consensus among physicists previously, it was experimentally confirmed that gravity attracts both matter and antimatter at the same rate within experimental error.
Bubble chamber experiments provide further evidence that antiparticles have the same inertial mass as their normal counterparts. In these experiments, the chamber is subjected to a constant magnetic field that causes charged particles to travel in helical paths, the radius and direction of which correspond to the ratio of electric charge to inertial mass. Particle–antiparticle pairs are seen to travel in helices with opposite directions but identical radii, implying that the ratios differ only in sign; but this does not indicate whether it is the charge or the inertial mass that is inverted. However, particle–antiparticle pairs are observed to electrically attract one another. This behavior implies that both have positive inertial mass and opposite charges; if the reverse were true, then the particle with positive inertial mass would be repelled from its antiparticle partner.
In quantum mechanics
In 1928, Paul Dirac's theory of elementary particles, now part of the Standard Model, already included negative solutions.[22] The Standard Model is a generalization of quantum electrodynamics (QED) and negative mass is already built into the theory.
Morris, Thorne and Yurtsever[23] pointed out that the quantum mechanics of the Casimir effect can be used to produce a locally mass-negative region of space–time. In this article, and subsequent work by others, they showed that negative matter could be used to stabilize a wormhole. Cramer et al. argue that such wormholes might have been created in the early universe, stabilized by negative-mass loops of cosmic string.[24] Stephen Hawking has argued that negative energy is a necessary condition for the creation of a closed timelike curve by manipulation of gravitational fields within a finite region of space;[25] this implies, for example, that a finite Tipler cylinder cannot be used as a time machine.
Schrödinger equation
For energy eigenstates of the Schrödinger equation, the wavefunction is wavelike wherever the particle's energy is greater than the local potential, and exponential-like (evanescent) wherever it is less. Naively, this would imply kinetic energy is negative in evanescent regions (to cancel the local potential). However, kinetic energy is an operator in quantum mechanics, and its expectation value is always positive, summing with the expectation value of the potential energy to yield the energy eigenvalue.
For wavefunctions of particles with zero rest mass (such as photons), this means that any evanescent portions of the wavefunction would be associated with a local negative mass–energy. However, the Schrödinger equation does not apply to massless particles; instead the Klein–Gordon equation is required.
In theory of vibrations and metamaterials
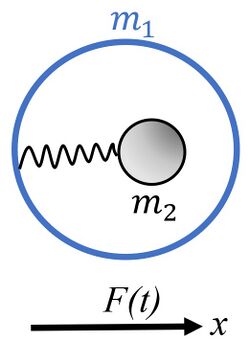
The mechanical model giving rise to the negative effective mass effect is depicted in Figure 1. A core with mass is connected internally through the spring with constant to a shell with mass . The system is subjected to the external sinusoidal force . If we solve the equations of motion for the masses and and replace the entire system with a single effective mass we obtain:[26][27][28][29] where .
When the frequency approaches from above the effective mass will be negative.[26][27][28][29]
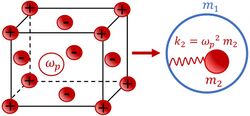
The negative effective mass (density) becomes also possible based on the electro-mechanical coupling exploiting plasma oscillations of a free electron gas (see Figure 2).[30][31] The negative mass appears as a result of vibration of a metallic particle with a frequency of which is close the frequency of the plasma oscillations of the electron gas relatively to the ionic lattice . The plasma oscillations are represented with the elastic spring , where is the plasma frequency.[30][31] Thus, the metallic particle vibrated with the external frequency ω is described by the effective mass
- ,
which is negative when the frequency ω approaches from above. Metamaterials exploiting the effect of the negative mass in the vicinity of the plasma frequency were reported.[30][31]
See also
- Dark fluid
- Imaginary mass
- Mirror matter
References
- ↑ Griffin, Andrew (2017-04-20). "Scientists observe liquid with 'negative mass', which turns physics completely backwards". https://www.independent.co.uk/news/science/negative-mass-object-washington-state-physics-isaac-newton-upside-down-a7693701.html.
- ↑ Mortillaro, Nicole (2017-04-20). "Scientists create fluid that seems to defy physics:'Negative mass' reacts opposite to any known physical property we know". http://www.cbc.ca/news/technology/fluid-negative-mass-1.4073937.
- ↑ Khanna, Gaurav (2019-01-28). "Time travel is possible – but only if you have an object with infinite mass". https://theconversation.com/time-travel-is-possible-but-only-if-you-have-an-object-with-infinite-mass-107063.
- ↑ University of Oxford (5 December 2018). "Bringing balance to the universe: New theory could explain missing 95 percent of the cosmos". EurekAlert!. https://www.eurekalert.org/pub_releases/2018-12/uoo-bbt120318.php.
- ↑ Farnes, J.S. (2018). "A Unifying Theory of Dark Energy and Dark Matter: Negative Masses and Matter Creation within a Modified ΛCDM Framework". Astronomy & Astrophysics 620: A92. doi:10.1051/0004-6361/201832898. Bibcode: 2018A&A...620A..92F.
- ↑ Luttinger, J. M. (1951). "On "Negative" mass in the theory of gravitation". Gravity Research Foundation. https://static1.squarespacewebcom/static/5852e579be659442a01f27b8/t/5873dc04d1758eea4b41c720/1483987972731/luttinger.pdf.
- ↑ 7.0 7.1 7.2 7.3 Bondi, H. (1957). "Negative Mass in General Relativity". Reviews of Modern Physics 29 (3): 423–428. doi:10.1103/RevModPhys.29.423. Bibcode: 1957RvMP...29..423B. http://ayuba.fr/pdf/bondi1957.pdf.
- ↑ Price, R. M. (1993). "Negative mass can be positively amusing". Am. J. Phys. 61 (3): 216. doi:10.1119/1.17293. Bibcode: 1993AmJPh..61..216P. http://people.westminstercollege.edu/faculty/ccline/courses/resources/wp/pdf/AJP000216.pdf.
- ↑ Shoen, R.; Yao, S.-T. (1979). "On the proof of the positive mass conjecture in general relativity". Commun. Math. Phys. 65 (1): 45–76. doi:10.1007/BF01940959. Bibcode: 1979CMaPh..65...45S. http://www.doctoryau.com/papers/PositiveMassConjecture.pdf. Retrieved 20 December 2014.
- ↑ Witten, Edward (1981). "A new proof of the positive energy theorem". Comm. Math. Phys. 80 (3): 381–402. doi:10.1007/bf01208277. Bibcode: 1981CMaPh..80..381W. http://projecteuclid.org/euclid.cmp/1103919981.
- ↑ Belletête, Jonathan; Paranjape, Manu (2013). "On Negative Mass". Int. J. Mod. Phys. D 22 (12): 1341017. doi:10.1142/S0218271813410174. Bibcode: 2013IJMPD..2241017B.
- ↑ Mbarek, Saoussen; Paranjape, Manu (2014). "Negative Mass Bubbles in De Sitter Spacetime". Phys. Rev. D 90 (10): 101502. doi:10.1103/PhysRevD.90.101502. Bibcode: 2014PhRvD..90j1502M.
- ↑ Bonnor, W. B.; Swaminarayan, N. S. (June 1964). "An exact solution for uniformly accelerated particles in general relativity". Zeitschrift für Physik 177 (3): 240–256. doi:10.1007/BF01375497. Bibcode: 1964ZPhy..177..240B.
- ↑ 14.0 14.1 14.2 Bonnor, W. B. (1989). "Negative mass in general relativity". General Relativity and Gravitation 21 (11): 1143–1157. doi:10.1007/BF00763458. Bibcode: 1989GReGr..21.1143B.
- ↑ 15.0 15.1 Forward, R. L. (1990). "Negative matter propulsion". Journal of Propulsion and Power 6: 28–37. doi:10.2514/3.23219.
- ↑ Bondi, H.; Bergmann, P.; Gold, T.; Pirani, F. (January 1957). "Negative mass in general relativity". in M. DeWitt, Cécile; Rickles, Dean. The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference. Open Access Epubli 2011. ISBN 978-3869319636. http://www.edition-open-sources.org/sources/5/24/index.html. Retrieved 21 December 2018.
- ↑ Landis, G. (1991). "Comments on Negative Mass Propulsion". J. Propulsion and Power 7 (2): 304. doi:10.2514/3.23327.
- ↑ Sakharov, A.D. (1980). " " (in ru). ZhETF 79: 689–693.[full citation needed]
translation in "Cosmological model of the Universe with a time vector inversion" (in en). JETP Lett. 52: 349–351. 1980.[full citation needed] - ↑ Barbour, Julian; Koslowski, Tim; Mercati, Flavio (2014). "Identification of a Gravitational Arrow of Time". Physical Review Letters 113 (18): 181101. doi:10.1103/PhysRevLett.113.181101. PMID 25396357. Bibcode: 2014PhRvL.113r1101B.
- ↑ 20.0 20.1 Hossenfelder, S. (15 August 2008). "A Bi-Metric Theory with Exchange Symmetry". Physical Review D 78 (4): 044015. doi:10.1103/PhysRevD.78.044015. Bibcode: 2008PhRvD..78d4015H.
- ↑ Andersson, E. K.; Baker, C. J.; Bertsche, W.; Bhatt, N. M. (September 27, 2023). "Observation of the effect of gravity on the motion of antimatter.". Nature 621 (7980): 716–722. doi:10.1038/s41586-023-06527-1. PMID 37758891. Bibcode: 2023Natur.621..716A.
- ↑ Dirac, P. A. M. (1928). "The Quantum Theory of the Electron". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 117 (778): 610–624. doi:10.1098/rspa.1928.0023. Bibcode: 1928RSPSA.117..610D.
- ↑ Morris, Michael S.; Thorne, Kip S.; Yurtsever, Ulvi (1988). "Wormholes, Time Machines, and the Weak Energy Condition". Physical Review Letters 61 (13): 1446–1449. doi:10.1103/PhysRevLett.61.1446. PMID 10038800. Bibcode: 1988PhRvL..61.1446M. https://authors.library.caltech.edu/9262/1/MORprl88.pdf.
- ↑ Cramer, John G.; Forward, Robert L.; Morris, Michael S.; Visser, Matt; Benford, Gregory; Landis, Geoffrey A. (1995). "Natural wormholes as gravitational lenses". Physical Review D 51 (6): 3117–3120. doi:10.1103/PhysRevD.51.3117. PMID 10018782. Bibcode: 1995PhRvD..51.3117C.
- ↑ Hawking, Stephen (2002). The Future of Spacetime. W. W. Norton. pp. 96. ISBN 978-0-393-02022-9. https://archive.org/details/futureofspacetim0000unse/page/96.
- ↑ 26.0 26.1 Milton, Graeme W; Willis, John R (2007-03-08). "On modifications of Newton's second law and linear continuum elastodynamics". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 463 (2079): 855–880. doi:10.1098/rspa.2006.1795. Bibcode: 2007RSPSA.463..855M. https://royalsocietypublishing.org/doi/10.1098/rspa.2006.1795.
- ↑ 27.0 27.1 Chan, C. T.; Li, Jensen; Fung, K. H. (2006-01-01). "On extending the concept of double negativity to acoustic waves" (in en). Journal of Zhejiang University Science A 7 (1): 24–28. doi:10.1631/jzus.2006.A0024. ISSN 1862-1775. https://doi.org/10.1631/jzus.2006.A0024.
- ↑ 28.0 28.1 Huang, H. H.; Sun, C. T.; Huang, G. L. (2009-04-01). "On the negative effective mass density in acoustic metamaterials" (in en). International Journal of Engineering Science 47 (4): 610–617. doi:10.1016/j.ijengsci.2008.12.007. ISSN 0020-7225. http://www.sciencedirect.com/science/article/pii/S0020722508002279.
- ↑ 29.0 29.1 Yao, Shanshan; Zhou, Xiaoming; Hu, Gengkai (2008-04-14). "Experimental study on negative effective mass in a 1D mass–spring system". New Journal of Physics 10 (4): 043020. doi:10.1088/1367-2630/10/4/043020. ISSN 1367-2630. Bibcode: 2008NJPh...10d3020Y.
- ↑ 30.0 30.1 30.2 Bormashenko, Edward; Legchenkova, Irina (April 2020). "Negative Effective Mass in Plasmonic Systems" (in en). Materials 13 (8): 1890. doi:10.3390/ma13081890. PMID 32316640. Bibcode: 2020Mate...13.1890B.
- ↑ 31.0 31.1 31.2 Bormashenko, Edward; Legchenkova, Irina; Frenkel, Mark (August 2020). "Negative Effective Mass in Plasmonic Systems II: Elucidating the Optical and Acoustical Branches of Vibrations and the Possibility of Anti-Resonance Propagation" (in en). Materials 13 (16): 3512. doi:10.3390/ma13163512. PMID 32784869. Bibcode: 2020Mate...13.3512B.
External links
 |

