Physics:Non ideal compressible fluid dynamics

From HandWiki
Non-monotone evolution of the Mach number M in the divergent section of a supersonic nozzle. The fluid is siloxane MM (hexamethyldisiloxane, [math]\ce{ C6H18OSi2 }[/math]) evolving in the non-ideal gasdynamic regime.

Non ideal compressible fluid dynamics (NICFD), or non ideal gas dynamics, is a branch of fluid mechanics studying the dynamic behavior of fluids not obeying ideal-gas thermodynamics. It is for example the case of dense vapors, supercritical flows and compressible two-phase flows. With the term dense vapors, we indicate all fluids in the gaseous state characterized by thermodynamic conditions close to saturation and the critical point.[1] Supercritical fluids feature instead values of pressure and temperature larger than their critical values,[2] whereas two-phase flows are characterized by the simultaneous presence of both liquid and gas phases.[3]

In all these cases, the fluid requires to be modelled as a real gas, since its thermodynamic behavior considerably differs from that of an ideal gas, which by contrast appears for dilute thermodynamic conditions. The ideal-gas law can be employed in general as a reasonable approximation of the fluid thermodynamics for low pressures and high temperatures. Otherwise, intermolecular forces and dimension of fluid particles, which are neglected in the ideal-gas approximation, become relevant and can significantly affect the fluid behavior.[4] This is extremely valid for gases made of complex and heavy molecules, which tend to deviate more from the ideal model.[5]

While the fluid dynamics of compressible flows in ideal conditions is well-established and is characterized by several analytical results,[6] when non-ideal thermodynamic conditions are considered, peculiar phenomena possibly occur. This is particularly valid in supersonic conditions, namely for flow velocities larger than the speed of sound in the fluid considered. All typical features of supersonic flows are affected by non-ideal thermodynamics, resulting in both quantitative and qualitative differences with respect to the ideal gas dynamics.[7]

Non-ideal thermodynamics

Main page: Physics:Real gas
Compressibility factor Z for different values of reduced pressure and temperature.

For dilute thermodynamic conditions, the ideal-gas equation of state (EoS) provides sufficiently accurate results in modelling the fluid thermodynamics. This occurs in general for low values of reduced pressure and high values of reduced temperature, where the term reduced refers to the ratio of a certain thermodynamic quantity and its critical value. For some fluids such as air, the assumption of considering ideal conditions is perfectly reasonable and it is widely used.[6]

On the other hand, when thermodynamic conditions approach condensation and the critical point or when high pressures are involved, real-gas models are needed in order to capture the real fluid behavior. In these conditions, in fact, intermolecular forces and compressibility effects come into play.[4]

A measure of the fluid non-ideality is given by the compressibility factor [math]\displaystyle{ Z }[/math],[8] defined as

[math]\displaystyle{ Z = \frac{Pv}{RT} }[/math]

where

  • [math]\displaystyle{ P }[/math] is the pressure [Pa];
  • [math]\displaystyle{ v }[/math] is the specific volume [m3/kg];
  • [math]\displaystyle{ R }[/math] is the specific gas constant [J/(kg K)], namely the universal gas constant divided by the fluid's molecular mass;
  • [math]\displaystyle{ T }[/math] is the absolute temperature [K].

The compressibility factor is a dimensionless quantity which is equal to 1 for ideal gases and deviates from unity for increasing levels of non-ideality.[9]

Several non-ideal models exist, from the simplest cubic equations of state (such as the Van der Waals[4][10] and the Peng-Robinson[11] models) up to complex multi-parameter ones, including the Span-Wagner equation of state.[12][13]

State-of-the-art equations of state are easily accessible through thermodynamic libraries, such as FluidProp or the open-source software CoolProp.[14]

Non-ideal gasdynamic regimes

The dynamic behavior of compressible flows is governed by the dimensionless thermodynamic quantity [math]\displaystyle{ \Gamma }[/math], which is known as the fundamental derivative of gasdynamics[15] and is defined as

[math]\displaystyle{ \Gamma = \frac{v^3}{2c^2} \left(\frac{\partial^2 P}{\partial v^2} \right)_s = 1+ \frac{c}{v} \left(\frac{\partial c}{\partial P} \right)_s }[/math]

where

  • [math]\displaystyle{ c }[/math] is the speed of sound [m/s];
  • [math]\displaystyle{ s }[/math] is the specific entropy per unit mass [J/(kg K)].

From a mathematical point of view, the fundamental derivative is a non-dimensional measure of the curvature of isentropes in the pressure-volume thermodynamic plane. From a physical point of view, the definition of [math]\displaystyle{ \Gamma }[/math] tells that the speed of sound increases with pressure in isentropic transformations for values of [math]\displaystyle{ \Gamma \gt 1 }[/math], while, by contrast, it decreases with pressure for [math]\displaystyle{ \Gamma \lt 1 }[/math].

Based on the value of [math]\displaystyle{ \Gamma }[/math], three gasdynamic regimes can be defined:[15]

  • ideal gasdynamic regime for [math]\displaystyle{ \Gamma \gt 1 }[/math];
  • non-ideal classical gasdynamic regime for [math]\displaystyle{ 0 \lt \Gamma \lt 1 }[/math];
  • non-classical gasdynamic regime for [math]\displaystyle{ \Gamma \lt 0 }[/math].

Ideal gasdynamic regime

In the ideal regime, the usual ideal-gas behavior is qualitatively recovered. For an ideal gas, in fact, the value of the fundamental derivative reduces to the constant value [math]\displaystyle{ \Gamma = \frac{\gamma + 1}{2} }[/math], where [math]\displaystyle{ \gamma }[/math] is the heat capacity ratio. By definition, [math]\displaystyle{ \gamma }[/math] is the ratio between the constant pressure and the constant volume specific heats, so it is larger than 1, leading to a value of [math]\displaystyle{ \Gamma }[/math] larger than 1 too.[6]

In this regime, only quantitative differences with respect to the ideal model are encountered. The flow evolution in fact depends on total, or stagnation, thermodynamic conditions. For example, the Mach number evolution of an ideal gas in a supersonic nozzle depends only on the heat capacity ratio (namely on the fluid) and on the exhaust-to-stagnation pressure ratio.[6] Considering real-gas effects, instead, even fixing the fluid and the pressure ratio, different total states yield different Mach profiles.[16]

Typically, for single-phase fluids made of simple molecules, only the ideal gasdynamic regime can be reached, even for thermodynamic conditions very close to saturation. It is for example the case of diatomic or triatomic molecules, such as nitrogen or carbon dioxide, which can only experience small departure from the ideal behavior.[5]

Non-ideal classical gasdynamic regime

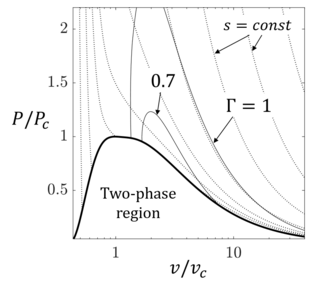
Reduced pressure-volume thermodynamic diagram for siloxane fluid MM (hexamethyldisiloxane, [math]\ce{ C6H18OSi2 }[/math]), including the liquid-vapor saturation curve, some isentropes and some isolines of the fundamental derivative of gas dynamics [math]\displaystyle{ \Gamma }[/math]. The non-ideal gas region ([math]\displaystyle{ 0 \lt \Gamma \lt 1 }[/math]) is shown close to the saturation curve.

For fluids with high molecular complexity, state-of-the-art thermodynamic models predict values of [math]\displaystyle{ 0 \lt \Gamma \lt 1 }[/math] in the single-phase region close to the saturation curve, where the speed of sound is largely sensitive to density variations along isentropes.[17] Such fluids belong to different classes of chemical compounds, including hydrocarbons, siloxanes and refrigerants.[5][17]

In the non-ideal regime, even qualitative differences with respect to ideal gasdynamics can be found, meaning that the flow evolution can be strongly different for varying total conditions. The most peculiar phenomenon of the non-ideal regime is the decrease of the Mach number in isentropic expansions occurring in the supersonic regime, namely processes in which the fluid density decreases.[18] Indeed, for an ideal gas expanding isentropically in a converging-diverging nozzle, the Mach number increases monotonically as the density decreases.[6] By contrast, for flows evolving in the non-ideal regime, a non-monotone Mach number evolution is possible in the divergent section, whereas the density reduction remains monotonic (see figure in the lead section). This particular phenomenon is governed by the quantity [math]\displaystyle{ J }[/math], which is a non-dimensional measure of the Mach number derivative with respect to density in isentropic processes:[18]

[math]\displaystyle{ J = \frac{\rho}{M} \frac{dM}{d \rho} = 1-\Gamma - \frac{1}{M^2} }[/math]

where

  • [math]\displaystyle{ M }[/math] is the Mach number;
  • [math]\displaystyle{ \rho }[/math] is the density [kg/m3].

From the definition of [math]\displaystyle{ J }[/math], the Mach number increases with density for flow conditions featuring values of [math]\displaystyle{ J\gt 0 }[/math]. Indeed, this is possible only for values of [math]\displaystyle{ \Gamma \lt 1 }[/math], that is in the non-ideal regime. However, this is not a sufficient condition for the non-monotone Mach number to appear, since a sufficiently large value of [math]\displaystyle{ M }[/math] is also required. In particular, supersonic conditions ([math]\displaystyle{ M \gt 1 }[/math]) are necessary.[18]

An analogous effect is encountered in the expansion around rarefactive ramps: for suitable thermodynamic conditions, the Mach number downstream of the ramp can be lower than the one upstream.[19] By contrast, in oblique shock waves, the post-shock Mach number can be larger than the pre-shock one.[20]

Non-classical gas-dynamic regime

Finally, fluids with an even higher molecular complexity can exhibit non-classical behavior in the single-phase vapor region near saturation. They are called Bethe-Zel’dovich-Thompson (BZT) fluids, from the name of physicists Hans Bethe,[21] Yakov Zel'dovich,[22] and Philip Thompson,[23][24] who first worked on these kinds of fluids.

For thermodynamic conditions lying in the non-classical regime, the non-monotone evolution of the Mach number in isentropic expansions can be found even in subsonic conditions. In fact, for values of [math]\displaystyle{ \Gamma \lt 0 }[/math], positive values of [math]\displaystyle{ J }[/math] can be reached also in subsonic flows ([math]\displaystyle{ M \lt 1 }[/math]). In other words, the non-monotone Mach number evolution is also possible in the convergent section of an isentropic nozzle.[24]

Moreover, a peculiar phenomenon of the non-classical regime is the so-called inverted gas-dynamics. In the classical regime, expansions are smooth isentropic processes, while compressions occur through shock waves, which are discontinuities in the flow. If gas-dynamics is inverted, the opposite occurs, namely rarefaction shock waves are physically admissible and compressions occur through smooth isentropic processes.[23]

As a consequence of the negative value of [math]\displaystyle{ \Gamma }[/math], two other peculiar phenomena can occur for BZT fluids: shock splitting and composite waves. Shock splitting occurs when an inadmissible pressure discontinuity evolves in time by generating two weaker shock waves.[25][26] Composite waves, instead, are referred to as phenomena in which two elementary waves propagate as a single entity.[7][27]

Experimental evidence of a non-classical gas-dynamic regime is not available yet. The main reasons are the complexity of performing experiments in such challenging thermodynamic conditions and the thermal stability of these very complex molecules.[28]

Applications

Compressible flows in non-ideal conditions are encountered in several industrial and aerospace applications. They are employed for example in Organic Rankine Cycles (ORC)[29] and supercritical carbon dioxide (sCO2) systems[30] for power production. In the aerospace field, fluids in conditions close to saturation can be used as oxiders in hybrid rocket motors or for surface cooling of rocket nozzles.[31] Gases made of molecules of high molecular mass can be used in supersonic wind tunnels instead of air to obtain higher Reynolds numbers.[32] Finally, non-ideal flows find application in fuels transportation at high-speed and in Rapid Expansion of Supercritical Solutions (RESS) of CO2 for particles generation or extraction of chemicals.[33]

Organic Rankine cycles

Main page: Physics:Organic Rankine cycle
ORC turbogenerator at the LUT University in Lappenranta, Finland .[34]

Usual Rankine cycles are thermodynamic cycles that employ water as a working fluid to produce electric power from thermal sources.[35] In Organic Rankine cycles, by contrast, water is substituted by molecularly complex organic compounds. Since the vaporization temperature of these kinds of fluids is lower than that of water at atmospheric pressure, low-to-medium temperature sources can be exploited allowing for heat recovery, for example, from biomass combustion, industrial waste heat, or geothermal heat.[36] For these reasons, ORC technology belongs to the class of renewable energies.

For the design of mechanical components, such as turbines, working in ORC plants, it is fundamental to take into account typical non-ideal gas-dynamic phenomena. In fact, the single-phase vapor at the inlet of an ORC turbine stator usually evolves in the non-ideal thermodynamic region close to the liquid-vapor saturation curve and critical point. Moreover, due to the high molecular mass of the complex organic compounds employed, the speed of sound in these fluids is low compared to that of air and other simple gases. Therefore, turbine stators are very likely to involve supersonic flows even if rather low flow velocities are reached.[37] High supersonic flows can produce large losses and mechanical stresses in the turbine blades due to the occurrence of shock waves, which cause a strong pressure raise.[38] However, when working fluids of the BZT class are employed, expander performances could be improved by exploiting some non-classical phenomena.[39][40]

Supercritical carbon dioxide cycles

When carbon dioxide is held above its critical pressure (73.773 bar)[41] and temperature (30.9780 °C),[41] it can behave both as a gas and as a liquid, that is it expands to fill entirely its container like a gas but has a density similar to that of a liquid.

Supercritical CO2 is chemically stable, very cheap, and non-flammable, making it suitable as a working fluid for transcritical cycles.[42] For example, it is employed in domestic water heat pumps, which can reach high efficiencies.[42]

Moreover, when used in power generation plants that employ Brayton and Rankine cycles, it can improve efficiency and power output. Its high density enables a strong reduction in turbomachines dimensions, still ensuring the high efficiency of these components. Simpler designs can therefore be adopted, while steam turbines require multiple turbine stages, which necessarily yield larger dimensions and costs.[43]

By contrast, mechanical components within sCO2 Brayton cycles, especially turbomachinery and heat exchangers, suffer from corrosion.[44]

See also

References

  1. ↑ Callen, Herbert B. (1985). Thermodynamics and an introduction to thermostatistics (2nd ed.). New York: J. Wiley & Sons. pp. 255–261. ISBN 978-0-471-86256-7. 
  2. ↑ Schlosky, Kevin M. (1989). "Supercritical phase transitions at very high pressure" (in en). Journal of Chemical Education 66 (12): 989. doi:10.1021/ed066p989. ISSN 0021-9584. Bibcode: 1989JChEd..66..989S. https://pubs.acs.org/doi/abs/10.1021/ed066p989. 
  3. ↑ Faghri, Amir; Zhang, Yuwen (2006-01-01), Faghri, Amir; Zhang, Yuwen, eds., "Two-Phase Flow and Heat Transfer" (in en), Transport Phenomena in Multiphase Systems (Boston: Academic Press): pp. 853–949, doi:10.1016/b978-0-12-370610-2.50016-7, ISBN 978-0-12-370610-2, https://www.sciencedirect.com/science/article/pii/B9780123706102500167, retrieved 2023-07-06 
  4. ↑ 4.0 4.1 4.2 Waals, J. D. van der; Rowlinson, John Shipley (1988). On the continuity of the gaseous and liquid states. Studies in statistical mechanics. Amsterdam: North-Holland. ISBN 978-0-444-87077-3. 
  5. ↑ 5.0 5.1 5.2 Colonna, P.; Guardone, A. (2006). "Molecular interpretation of nonclassical gas dynamics of dense vapors under the van der Waals model". Physics of Fluids 18 (5): 056101–056101–14. doi:10.1063/1.2196095. ISSN 1070-6631. Bibcode: 2006PhFl...18e6101C. http://dx.doi.org/10.1063/1.2196095. 
  6. ↑ 6.0 6.1 6.2 6.3 6.4 Thompson, Philip A. (1972). Compressible-fluid dynamics. Advanced engineering series. New York: McGraw-Hill. pp. 76–99. ISBN 978-0-07-064405-2. 
  7. ↑ 7.0 7.1 Menikoff, Ralph; Plohr, Bradley J. (1989-01-01). "The Riemann problem for fluid flow of real materials". Reviews of Modern Physics 61 (1): 75–130. doi:10.1103/revmodphys.61.75. ISSN 0034-6861. Bibcode: 1989RvMP...61...75M. http://dx.doi.org/10.1103/revmodphys.61.75. 
  8. ↑ Zucker, Robert D.; Biblarz, Oscar (2002). Fundamentals of gas dynamics (2nd ed.). Hoboken, NJ: Wiley. pp. 327. ISBN 978-0-471-05967-7. 
  9. ↑ Thompson, Philip A. (1972). Compressible-fluid dynamics. Advanced engineering series. New York: McGraw-Hill. pp. 99–101. ISBN 978-0-07-064405-2. 
  10. ↑ Parsegian, V. Adrian (2005). Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. Cambridge: Cambridge University Press. doi:10.1017/cbo9780511614606. ISBN 978-0-521-83906-8. https://www.cambridge.org/core/books/van-der-waals-forces/EFAB2ADFEF0B97F2AEB112AA6F3A7862. 
  11. ↑ Peng, Ding-Yu; Robinson, Donald B. (February 1976). "A New Two-Constant Equation of State" (in en). Industrial & Engineering Chemistry Fundamentals 15 (1): 59–64. doi:10.1021/i160057a011. ISSN 0196-4313. https://pubs.acs.org/doi/abs/10.1021/i160057a011. 
  12. ↑ Span, R.; Wagner, W. (2003-01-01). "Equations of State for Technical Applications. I. Simultaneously Optimized Functional Forms for Nonpolar and Polar Fluids" (in en). International Journal of Thermophysics 24 (1): 1–39. doi:10.1023/A:1022390430888. ISSN 1572-9567. https://doi.org/10.1023/A:1022390430888. 
  13. ↑ Span, Roland (2000), "Describing Mixtures with Multiparameter Equations of State", Multiparameter Equations of State (Berlin, Heidelberg: Springer Berlin Heidelberg): pp. 319–340, doi:10.1007/978-3-662-04092-8_8, ISBN 978-3-642-08671-7, http://dx.doi.org/10.1007/978-3-662-04092-8_8, retrieved 2023-07-05 
  14. ↑ Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27). "Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp". Industrial & Engineering Chemistry Research 53 (6): 2498–2508. doi:10.1021/ie4033999. ISSN 0888-5885. PMID 24623957. PMC 3944605. http://dx.doi.org/10.1021/ie4033999. 
  15. ↑ 15.0 15.1 Thompson, Philip A. (1971). "A Fundamental Derivative in Gasdynamics". Physics of Fluids 14 (9): 1843–1849. doi:10.1063/1.1693693. ISSN 0031-9171. Bibcode: 1971PhFl...14.1843T. http://dx.doi.org/10.1063/1.1693693. 
  16. ↑ Tsien, Hsue-Shen (1946). "One-Dimensional Flows of a Gas Characterized by Vander Waal's Equation of State". Journal of Mathematics and Physics 25 (1–4): 301–324. doi:10.1002/sapm1946251301. ISSN 0097-1421. http://dx.doi.org/10.1002/sapm1946251301. 
  17. ↑ 17.0 17.1 Kluwick, Alfred (2004-05-01). "Internal flows of dense gases". Acta Mechanica 169 (1–4): 123–143. doi:10.1007/s00707-004-0096-z. ISSN 0001-5970. http://dx.doi.org/10.1007/s00707-004-0096-z. 
  18. ↑ 18.0 18.1 18.2 Cramer, M. S.; Best, L. M. (1991). "Steady, isentropic flows of dense gases". Physics of Fluids A: Fluid Dynamics 3 (1): 219–226. doi:10.1063/1.857855. ISSN 0899-8213. Bibcode: 1991PhFlA...3..219C. http://dx.doi.org/10.1063/1.857855. 
  19. ↑ Cramer, M. S.; Crickenberger, A. B. (1992). "Prandtl-Meyer function for dense gases". AIAA Journal 30 (2): 561–564. doi:10.2514/3.10956. ISSN 0001-1452. Bibcode: 1992AIAAJ..30..561C. http://dx.doi.org/10.2514/3.10956. 
  20. ↑ Vimercati, Davide; Gori, Giulio; Guardone, Alberto (2018-05-21). "Non-ideal oblique shock waves". Journal of Fluid Mechanics 847: 266–285. doi:10.1017/jfm.2018.328. ISSN 0022-1120. Bibcode: 2018JFM...847..266V. http://dx.doi.org/10.1017/jfm.2018.328. 
  21. ↑ Bethe, H. A. (1998), "On the Theory of Shock Waves for an Arbitrary Equation of State", Classic Papers in Shock Compression Science (New York, NY: Springer New York): pp. 421–495, doi:10.1007/978-1-4612-2218-7_11, ISBN 978-1-4612-7461-2, http://dx.doi.org/10.1007/978-1-4612-2218-7_11, retrieved 2023-07-05 
  22. ↑ "14. On the Possibility of Rarefaction Shock Waves", Selected Works of Yakov Borisovich Zeldovich, Volume I (Princeton University Press): pp. 152–154, 1992-12-31, doi:10.1515/9781400862979.152, ISBN 9781400862979, http://dx.doi.org/10.1515/9781400862979.152, retrieved 2023-07-05 
  23. ↑ 23.0 23.1 Thompson, P. A.; Lambrakis, K. C. (1973-08-21). "Negative shock waves". Journal of Fluid Mechanics 60 (1): 187–208. doi:10.1017/s002211207300011x. ISSN 0022-1120. Bibcode: 1973JFM....60..187T. http://dx.doi.org/10.1017/s002211207300011x. 
  24. ↑ 24.0 24.1 Lambrakis, Konstantine C. (1972). "Existence of Real Fluids with a Negative Fundamental Derivative Γ". Physics of Fluids 15 (5): 933–935. doi:10.1063/1.1694004. ISSN 0031-9171. Bibcode: 1972PhFl...15..933L. 
  25. ↑ Cramer, M. S. (February 1989). "Shock splitting in single-phase gases". Journal of Fluid Mechanics 199: 281–296. doi:10.1017/s0022112089000388. ISSN 0022-1120. Bibcode: 1989JFM...199..281C. http://dx.doi.org/10.1017/s0022112089000388. 
  26. ↑ Cramer, M. S. (1991), "Nonclassical Dynamics of Classical Gases", Nonlinear Waves in Real Fluids (Vienna: Springer Vienna): pp. 91–145, doi:10.1007/978-3-7091-2608-0_5, ISBN 978-3-211-82277-7, http://dx.doi.org/10.1007/978-3-7091-2608-0_5, retrieved 2023-07-05 
  27. ↑ KLUWICK, ALFRED (2001), "Rarefaction Shocks", Handbook of Shock Waves (Elsevier): pp. 339–411, doi:10.1016/b978-012086430-0/50008-7, ISBN 9780120864300, http://dx.doi.org/10.1016/b978-012086430-0/50008-7 
  28. ↑ Borisov, A. A.; Borisov, Al. A.; Kutateladze, S. S.; Nakoryakov, V. E. (January 1983). "Rarefaction shock wave near the critical liquid–vapour point". Journal of Fluid Mechanics 126: 59–73. doi:10.1017/s002211208300004x. ISSN 0022-1120. Bibcode: 1983JFM...126...59B. http://dx.doi.org/10.1017/s002211208300004x. 
  29. ↑ Angelino, G.; Invernizzi, C.; Macchi, E. (1991), "Organic Working Fluid Optimization for Space Power Cycles", Modern Research Topics in Aerospace Propulsion (New York, NY: Springer New York): pp. 297–326, doi:10.1007/978-1-4612-0945-4_16, ISBN 978-1-4612-6956-4, http://dx.doi.org/10.1007/978-1-4612-0945-4_16, retrieved 2023-07-05 
  30. ↑ Feher, E.G. (1968). "The supercritical thermodynamic power cycle". Energy Conversion 8 (2): 85–90. doi:10.1016/0013-7480(68)90105-8. ISSN 0013-7480. http://dx.doi.org/10.1016/0013-7480(68)90105-8. 
  31. ↑ "Rocket Propulsion Elements. 2nd edition. George P. Sutton. J. Wiley and Sons Inc., New York, 1956. 483 pp. Illustrated. 82s.". The Journal of the Royal Aeronautical Society 61 (559): 503. 1957. doi:10.1017/s0368393100128512. ISSN 0368-3931. http://dx.doi.org/10.1017/s0368393100128512. 
  32. ↑ Sagnier, P.; Vérant, J.-L. (1998). "On the validation of high enthalpy wind tunnel simulations". Aerospace Science and Technology 2 (7): 425–437. doi:10.1016/s1270-9638(99)80002-9. ISSN 1270-9638. http://dx.doi.org/10.1016/s1270-9638(99)80002-9. 
  33. ↑ Helfgen, B.; Türk, M.; Schaber, K. (2003). "Hydrodynamic and aerosol modelling of the rapid expansion of supercritical solutions (RESS-process)". The Journal of Supercritical Fluids 26 (3): 225–242. doi:10.1016/s0896-8446(02)00159-6. ISSN 0896-8446. http://dx.doi.org/10.1016/s0896-8446(02)00159-6. 
  34. ↑ Turunen-Saaresti, Teemu; Uusitalo, Antti; Honkatukia, Juha (2017). "Design and testing of high temperature micro-ORC test stand using Siloxane as working fluid". Journal of Physics: Conference Series 821 (1): 012024. doi:10.1088/1742-6596/821/1/012024. ISSN 1742-6588. Bibcode: 2017JPhCS.821a2024T. 
  35. ↑ Saitoh, T.S.; Hoshi, A. (2004). "Proposed solar Rankine cycle system with phase change steam accumulator and CPC solar collector". IECEC '02. 2002 37th Intersociety Energy Conversion Engineering Conference, 2002. IEEE. pp. 725–730. doi:10.1109/iecec.2002.1392137. ISBN 0-7803-7296-4. http://dx.doi.org/10.1109/iecec.2002.1392137. 
  36. ↑ Quoilin, Sylvain; Broek, Martijn Van Den; Declaye, Sébastien; Dewallef, Pierre; Lemort, Vincent (2013). "Techno-economic survey of Organic Rankine Cycle (ORC) systems". Renewable and Sustainable Energy Reviews 22: 168–186. doi:10.1016/j.rser.2013.01.028. ISSN 1364-0321. 
  37. ↑ Brown, Brady; Argrow, Brian (1999-01-11). "Application of Bethe-Zel'dovich-Thompson fluids in organic Rankine cycle engines". 37th Aerospace Sciences Meeting and Exhibit (Reston, Virigina: American Institute of Aeronautics and Astronautics). doi:10.2514/6.1999-462. http://dx.doi.org/10.2514/6.1999-462. 
  38. ↑ Denton, J. D.; Xu, L. (1989-06-04). "The Trailing Edge Loss of Transonic Turbine Blades". Proceedings of the ASME 1989 International Gas Turbine and Aeroengine Congress and Exposition. Volume 1: Turbomachinery. American Society of Mechanical Engineers. doi:10.1115/89-gt-278. ISBN 978-0-7918-7913-9. http://dx.doi.org/10.1115/89-gt-278. 
  39. ↑ Kluwick, A. (1994), "Interacting laminar boundary layers of dense gases", Fluid- and Gasdynamics (Vienna: Springer Vienna): pp. 335–349, doi:10.1007/978-3-7091-9310-5_37, ISBN 978-3-211-82495-5, http://dx.doi.org/10.1007/978-3-7091-9310-5_37, retrieved 2023-07-06 
  40. ↑ CRAMER, M. S.; PARK, S. (1999). "On the suppression of shock-induced separation in Bethe–Zel'dovich–Thompson fluids". Journal of Fluid Mechanics 393 (1): 1–21. doi:10.1017/s0022112099005479. ISSN 0022-1120. Bibcode: 1999JFM...393....1C. http://dx.doi.org/10.1017/s0022112099005479. 
  41. ↑ 41.0 41.1 Span, Roland; Wagner, Wolfgang (1996-11-01). "A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa". Journal of Physical and Chemical Reference Data 25 (6): 1509–1596. doi:10.1063/1.555991. ISSN 0047-2689. http://dx.doi.org/10.1063/1.555991. 
  42. ↑ 42.0 42.1 Ma, Yitai; Liu, Zhongyan; Tian, Hua (2013). "A review of transcritical carbon dioxide heat pump and refrigeration cycles". Energy 55: 156–172. doi:10.1016/j.energy.2013.03.030. ISSN 0360-5442. http://dx.doi.org/10.1016/j.energy.2013.03.030. 
  43. ↑ Fleming, Darryn; Pasch, Jim; Conboy, Thomas; Carlson, Matt (2013-06-03). "Testing Platform and Commercialization Plan for Heat Exchanging Systems for SCO2 Power Cycles". Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. Volume 8: Supercritical CO2 Power Cycles; Wind Energy; Honors and Awards. American Society of Mechanical Engineers. doi:10.1115/gt2013-95125. ISBN 978-0-7918-5529-4. http://dx.doi.org/10.1115/gt2013-95125. 
  44. ↑ Fleming, Darryn; Kruizenga, Alan; Pasch, James; Conboy, Tom; Carlson, Matt (2014-06-16). "Corrosion and Erosion Behavior in Supercritical CO2 Power Cycles". Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. Volume 3B: Oil and Gas Applications; Organic Rankine Cycle Power Systems; Supercritical CO2 Power Cycles; Wind Energy. doi:10.1115/gt2014-25136. ISBN 978-0-7918-4566-0. http://dx.doi.org/10.1115/gt2014-25136. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Non_ideal_compressible_fluid_dynamics&oldid=3276633"