Physics:Isentropic process
| Thermodynamics |
|---|
 |
In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible.[1][2][3][4][5][6] The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes.[7] This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such.
The word "isentropic" can be interpreted in another way, since its meaning is deducible from its etymology. It means a process in which the entropy of the system remains unchanged; as mentioned, this could occur if the process is both adiabatic and reversible. However, this could also occur in a system where the work done on the system includes friction internal to the system, and heat is withdrawn from the system in just the right amount to compensate for the internal friction, so as to leave the entropy unchanged.[8] However, in relation to the universe, the entropy of the universe would increase as a result, in agreement with the Second Law of Thermodynamics.
Background
The second law of thermodynamics states[9][10] that
- [math]\displaystyle{ T_\text{surr}dS \ge \delta Q, }[/math]
where [math]\displaystyle{ \delta Q }[/math] is the amount of energy the system gains by heating, [math]\displaystyle{ T_\text{surr} }[/math]is the temperature of the surroundings, and [math]\displaystyle{ dS }[/math] is the change in entropy. The equal sign refers to a reversible process, which is an imagined idealized theoretical limit, never actually occurring in physical reality, with essentially equal temperatures of system and surroundings.[11][12] For an isentropic process, if also reversible, there is no transfer of energy as heat because the process is adiabatic; δQ = 0. In contrast, if the process is irreversible, entropy is produced within the system; consequently, in order to maintain constant entropy within the system, energy must be simultaneously removed from the system as heat.
For reversible processes, an isentropic transformation is carried out by thermally "insulating" the system from its surroundings. Temperature is the thermodynamic conjugate variable to entropy, thus the conjugate process would be an isothermal process, in which the system is thermally "connected" to a constant-temperature heat bath.
Isentropic processes in thermodynamic systems
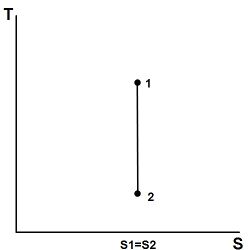
The entropy of a given mass does not change during a process that is internally reversible and adiabatic. A process during which the entropy remains constant is called an isentropic process, written [math]\displaystyle{ \Delta s=0 }[/math] or [math]\displaystyle{ s_1 = s_2 }[/math].[13] Some examples of theoretically isentropic thermodynamic devices are pumps, gas compressors, turbines, nozzles, and diffusers.
Isentropic efficiencies of steady-flow devices in thermodynamic systems
Most steady-flow devices operate under adiabatic conditions, and the ideal process for these devices is the isentropic process. The parameter that describes how efficiently a device approximates a corresponding isentropic device is called isentropic or adiabatic efficiency.[13]
Isentropic efficiency of turbines:
- [math]\displaystyle{ \eta_\text{t} = \frac{\text{actual turbine work}}{\text{isentropic turbine work}} = \frac{W_a}{W_s} \cong \frac{h_1 - h_{2a}}{h_1 - h_{2s}}. }[/math]
Isentropic efficiency of compressors:
- [math]\displaystyle{ \eta_\text{c} = \frac{\text{isentropic compressor work}}{\text{actual compressor work}} = \frac{W_s}{W_a} \cong \frac{h_{2s} - h_1}{h_{2a} - h_1}. }[/math]
Isentropic efficiency of nozzles:
- [math]\displaystyle{ \eta_\text{n} = \frac{\text{actual KE at nozzle exit}}{\text{isentropic KE at nozzle exit}} = \frac{V_{2a}^2}{V_{2s}^2} \cong \frac{h_1 - h_{2a}}{h_1 - h_{2s}}. }[/math]
For all the above equations:
- [math]\displaystyle{ h_1 }[/math] is the specific enthalpy at the entrance state,
- [math]\displaystyle{ h_{2a} }[/math] is the specific enthalpy at the exit state for the actual process,
- [math]\displaystyle{ h_{2s} }[/math] is the specific enthalpy at the exit state for the isentropic process.
Isentropic devices in thermodynamic cycles
| Cycle | Isentropic step | Description |
|---|---|---|
| Ideal Rankine cycle | 1→2 | Isentropic compression in a pump |
| Ideal Rankine cycle | 3→4 | Isentropic expansion in a turbine |
| Ideal Carnot cycle | 2→3 | Isentropic expansion |
| Ideal Carnot cycle | 4→1 | Isentropic compression |
| Ideal Otto cycle | 1→2 | Isentropic compression |
| Ideal Otto cycle | 3→4 | Isentropic expansion |
| Ideal Diesel cycle | 1→2 | Isentropic compression |
| Ideal Diesel cycle | 3→4 | Isentropic expansion |
| Ideal Brayton cycle | 1→2 | Isentropic compression in a compressor |
| Ideal Brayton cycle | 3→4 | Isentropic expansion in a turbine |
| Ideal vapor-compression refrigeration cycle | 1→2 | Isentropic compression in a compressor |
| Ideal Lenoir cycle | 2→3 | Isentropic expansion |
Note: The isentropic assumptions are only applicable with ideal cycles. Real cycles have inherent losses due to compressor and turbine inefficiencies and the second law of thermodynamics. Real systems are not truly isentropic, but isentropic behavior is an adequate approximation for many calculation purposes.
Isentropic flow
In fluid dynamics, an isentropic flow is a fluid flow that is both adiabatic and reversible. That is, no heat is added to the flow, and no energy transformations occur due to friction or dissipative effects. For an isentropic flow of a perfect gas, several relations can be derived to define the pressure, density and temperature along a streamline.
Note that energy can be exchanged with the flow in an isentropic transformation, as long as it doesn't happen as heat exchange. An example of such an exchange would be an isentropic expansion or compression that entails work done on or by the flow.
For an isentropic flow, entropy density can vary between different streamlines. If the entropy density is the same everywhere, then the flow is said to be homentropic.
Derivation of the isentropic relations
For a closed system, the total change in energy of a system is the sum of the work done and the heat added:
- [math]\displaystyle{ dU = \delta W + \delta Q. }[/math]
The reversible work done on a system by changing the volume is
- [math]\displaystyle{ \delta W = -p \,dV, }[/math]
where [math]\displaystyle{ p }[/math] is the pressure, and [math]\displaystyle{ V }[/math] is the volume. The change in enthalpy ([math]\displaystyle{ H = U + pV }[/math]) is given by
- [math]\displaystyle{ dH = dU + p \,dV + V \,dp. }[/math]
Then for a process that is both reversible and adiabatic (i.e. no heat transfer occurs), [math]\displaystyle{ \delta Q_\text{rev} = 0 }[/math], and so [math]\displaystyle{ dS = \delta Q_\text{rev}/T = 0 }[/math] All reversible adiabatic processes are isentropic. This leads to two important observations:
- [math]\displaystyle{ dU = \delta W + \delta Q = -p \,dV + 0, }[/math]
- [math]\displaystyle{ dH = \delta W + \delta Q + p \,dV + V \,dp = -p \,dV + 0 + p \,dV + V \,dp = V \,dp. }[/math]
Next, a great deal can be computed for isentropic processes of an ideal gas. For any transformation of an ideal gas, it is always true that
- [math]\displaystyle{ dU = n C_v \,dT }[/math], and [math]\displaystyle{ dH = n C_p \,dT. }[/math]
Using the general results derived above for [math]\displaystyle{ dU }[/math] and [math]\displaystyle{ dH }[/math], then
- [math]\displaystyle{ dU = n C_v \,dT = -p \,dV, }[/math]
- [math]\displaystyle{ dH = n C_p \,dT = V \,dp. }[/math]
So for an ideal gas, the heat capacity ratio can be written as
- [math]\displaystyle{ \gamma = \frac{C_p}{C_V} = -\frac{dp/p}{dV/V}. }[/math]
For a calorically perfect gas [math]\displaystyle{ \gamma }[/math] is constant. Hence on integrating the above equation, assuming a calorically perfect gas, we get
- [math]\displaystyle{ pV^\gamma = \text{constant}, }[/math]
that is,
- [math]\displaystyle{ \frac{p_2}{p_1} = \left(\frac{V_1}{V_2}\right)^\gamma. }[/math]
Using the equation of state for an ideal gas, [math]\displaystyle{ p V = n R T }[/math],
- [math]\displaystyle{ TV^{\gamma-1} = \text{constant}. }[/math]
(Proof: [math]\displaystyle{ PV^\gamma = \text{constant} \Rightarrow PV\,V^{\gamma-1} = \text{constant} \Rightarrow nRT\,V^{\gamma-1} = \text{constant}. }[/math] But nR = constant itself, so [math]\displaystyle{ TV^{\gamma-1} = \text{constant} }[/math].)
- [math]\displaystyle{ \frac{p^{\gamma-1}}{T^\gamma} = \text{constant} }[/math]
also, for constant [math]\displaystyle{ C_p = C_v + R }[/math] (per mole),
- [math]\displaystyle{ \frac{V}{T} = \frac{nR}{p} }[/math] and [math]\displaystyle{ p = \frac{nRT}{V} }[/math]
- [math]\displaystyle{ S_2-S_1 = nC_p \ln\left(\frac{T_2}{T_1}\right) - nR\ln\left(\frac{p_2}{p_1}\right) }[/math]
- [math]\displaystyle{ \frac{S_2-S_1}{n} = C_p \ln\left(\frac{T_2}{T_1}\right) - R\ln\left(\frac{T_2 V_1}{T_1 V_2}\right ) = C_v\ln\left(\frac{T_2}{T_1}\right)+ R \ln\left(\frac{V_2}{V_1}\right) }[/math]
Thus for isentropic processes with an ideal gas,
- [math]\displaystyle{ T_2 = T_1\left(\frac{V_1}{V_2}\right)^{(R/C_v)} }[/math] or [math]\displaystyle{ V_2 = V_1\left(\frac{T_1}{T_2}\right)^{(C_v/R)} }[/math]
Table of isentropic relations for an ideal gas
[math]\displaystyle{ \frac{T_2}{T_1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{P_2}{P_1} \right )^\frac {\gamma-1}{\gamma} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{V_1}{V_2} \right )^{(\gamma-1)} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{\rho_2}{\rho_1} \right )^{(\gamma - 1)} }[/math] [math]\displaystyle{ \left (\frac{T_2}{T_1} \right )^\frac {\gamma}{\gamma-1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \frac {P_2} {P_1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{V_1}{V_2} \right )^{\gamma} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{\rho_2}{\rho_1} \right )^{\gamma} }[/math] [math]\displaystyle{ \left (\frac{T_1}{T_2} \right )^\frac {1}{\gamma-1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{P_1}{P_2} \right )^\frac {1}{\gamma} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \frac{V_2}{V_1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \frac{\rho_1}{\rho_2} }[/math] [math]\displaystyle{ \left (\frac{T_2}{T_1} \right )^\frac {1}{\gamma-1} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \left (\frac{P_2}{P_1} \right )^\frac {1}{\gamma} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \frac{V_1}{V_2} }[/math] [math]\displaystyle{ = }[/math] [math]\displaystyle{ \frac{\rho_2}{\rho_1} }[/math]
Derived from
- [math]\displaystyle{ PV^{\gamma} = \text{constant}, }[/math]
- [math]\displaystyle{ PV = m R_s T, }[/math]
- [math]\displaystyle{ P = \rho R_s T, }[/math]
where:
- [math]\displaystyle{ P }[/math] = pressure,
- [math]\displaystyle{ V }[/math] = volume,
- [math]\displaystyle{ \gamma }[/math] = ratio of specific heats = [math]\displaystyle{ C_p/C_v }[/math],
- [math]\displaystyle{ T }[/math] = temperature,
- [math]\displaystyle{ m }[/math] = mass,
- [math]\displaystyle{ R_s }[/math] = gas constant for the specific gas = [math]\displaystyle{ R/M }[/math],
- [math]\displaystyle{ R }[/math] = universal gas constant,
- [math]\displaystyle{ M }[/math] = molecular weight of the specific gas,
- [math]\displaystyle{ \rho }[/math] = density,
- [math]\displaystyle{ C_p }[/math] = specific heat at constant pressure,
- [math]\displaystyle{ C_v }[/math] = specific heat at constant volume.
See also
Notes
- ↑ Partington, J. R. (1949), An Advanced Treatise on Physical Chemistry., 1, Fundamental Principles. The Properties of Gases, London: Longmans, Green and Co., p. 122.
- ↑ Kestin, J. (1966). A Course in Thermodynamics, Blaisdell Publishing Company, Waltham MA, p. 196.
- ↑ Münster, A. (1970). Classical Thermodynamics, translated by E. S. Halberstadt, Wiley–Interscience, London, ISBN:0-471-62430-6, p. 13.
- ↑ Haase, R. (1971). Survey of Fundamental Laws, chapter 1 of Thermodynamics, pages 1–97 of volume 1, ed. W. Jost, of Physical Chemistry. An Advanced Treatise, ed. H. Eyring, D. Henderson, W. Jost, Academic Press, New York, lcn 73–117081, p. 71.
- ↑ Borgnakke, C., Sonntag., R.E. (2009). Fundamentals of Thermodynamics, seventh edition, Wiley, ISBN:978-0-470-04192-5, p. 310.
- ↑ Massey, B. S. (1970), Mechanics of Fluids, Section 12.2 (2nd edition) Van Nostrand Reinhold Company, London. Library of Congress Catalog Card Number: 67-25005, p. 19.
- ↑ Çengel, Y. A., Boles, M. A. (2015). Thermodynamics: An Engineering Approach, 8th edition, McGraw-Hill, New York, ISBN:978-0-07-339817-4, p. 340.
- ↑ Çengel, Y. A., Boles, M. A. (2015). Thermodynamics: An Engineering Approach, 8th edition, McGraw-Hill, New York, ISBN:978-0-07-339817-4, pp. 340–341.
- ↑ Mortimer, R. G. Physical Chemistry, 3rd ed., p. 120, Academic Press, 2008.
- ↑ Fermi, E. Thermodynamics, footnote on p. 48, Dover Publications,1956 (still in print).
- ↑ Guggenheim, E. A. (1985). Thermodynamics. An Advanced Treatment for Chemists and Physicists, seventh edition, North Holland, Amsterdam, ISBN:0444869514, p. 12: "As a limiting case between natural and unnatural processes[,] we have reversible processes, which consist of the passage in either direction through a continuous series of equilibrium states. Reversible processes do not actually occur..."
- ↑ Kestin, J. (1966). A Course in Thermodynamics, Blaisdell Publishing Company, Waltham MA, p. 127: "However, by a stretch of imagination, it was accepted that a process, compression or expansion, as desired, could be performed 'infinitely slowly'[,] or as is sometimes said, quasistatically." P. 130: "It is clear that all natural processes are irreversible and that reversible processes constitute convenient idealizations only."
- ↑ 13.0 13.1 Cengel, Yunus A., and Michaeul A. Boles. Thermodynamics: An Engineering Approach. 7th Edition ed. New York: Mcgraw-Hill, 2012. Print.
References
- Van Wylen, G. J. and Sonntag, R. E. (1965), Fundamentals of Classical Thermodynamics, John Wiley & Sons, Inc., New York. Library of Congress Catalog Card Number: 65-19470
 |