Physics:Rotational frequency
| Rotational frequency | |
|---|---|
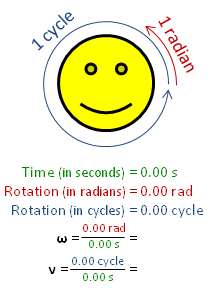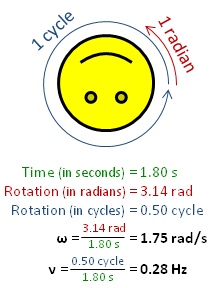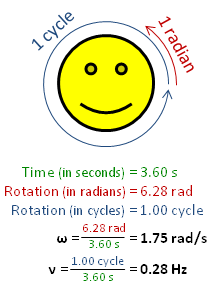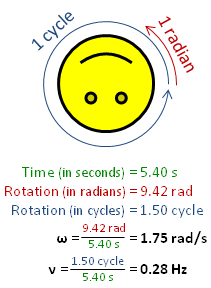 Angular speed ω (in radians per second), is greater than rotational frequency ν (in Hz), by a factor of 2π. | |
Common symbols | , n |
| SI unit | Hz |
Other units | rpm, cps |
| In SI base units | s-1 |
Derivations from other quantities | ν=ω/(2π rad), n=dN/dt |
| Part of a series on |
| Classical mechanics |
|---|
Rotational frequency, also known as rotational speed or rate of rotation (symbols ν, lowercase Greek nu, and also n), is the frequency of rotation of an object around an axis. Its SI unit is the reciprocal seconds (s−1); other common units of measurement include the hertz (Hz), cycles per second (cps), and revolutions per minute (rpm).[1][lower-alpha 1][lower-alpha 2]
Rotational frequency can be obtained dividing angular frequency, ω, by a full turn (2π radians): ν=ω/(2π rad). It can also be formulated as the instantaneous rate of change of the number of rotations, N, with respect to time, t: n=dN/dt (as per International System of Quantities).[4] Similar to ordinary period, the reciprocal of rotational frequency is the rotation period or period of rotation, T=ν−1=n−1, with dimension of time (SI unit seconds).
Rotational velocity is the vector quantity whose magnitude equals the scalar rotational speed. In the special cases of spin (around an axis internal to the body) and revolution (external axis), the rotation speed may be called spin speed and revolution speed, respectively.
Rotational acceleration is the rate of change of rotational velocity; it has dimension of squared reciprocal time and SI units of squared reciprocal seconds (s−2); thus, it is a normalized version of angular acceleration and it is analogous to chirpyness.
Related quantities
Tangential speed (Latin letter v), rotational frequency , and radial distance , are related by the following equation:[5]
An algebraic rearrangement of this equation allows us to solve for rotational frequency:
Thus, the tangential speed will be directly proportional to when all parts of a system simultaneously have the same , as for a wheel, disk, or rigid wand. The direct proportionality of to is not valid for the planets, because the planets have different rotational frequencies.
Regression analysis
Rotational frequency can measure, for example, how fast a motor is running. Rotational speed is sometimes used to mean angular frequency rather than the quantity defined in this article. Angular frequency gives the change in angle per time unit, which is given with the unit radian per second in the SI system. Since 2π radians or 360 degrees correspond to a cycle, we can convert angular frequency to rotational frequency by where
- is rotational frequency, with unit cycles per second
- is angular frequency, with unit radian per second or degree per second
For example, a stepper motor might turn exactly one complete revolution each second. Its angular frequency is 360 degrees per second (360°/s), or 2π radians per second (2π rad/s), while the rotational frequency is 60 rpm.
Rotational frequency is not to be confused with tangential speed, despite some relation between the two concepts. Imagine a merry-go-round with a constant rate of rotation. No matter how close to or far from the axis of rotation you stand, your rotational frequency will remain constant. However, your tangential speed does not remain constant. If you stand two meters from the axis of rotation, your tangential speed will be double the amount if you were standing only one meter from the axis of rotation.
See also
- Angular velocity
- Radial velocity
- Rotation period
- Rotational spectrum
- Tachometer
Notes
- ↑ "The rotational frequency n of a rotating body is defined to be the number of revolutions it makes in a time interval divided by that time interval [4: ISO 80000-3]. The SI unit of this quantity is thus the reciprocal second (s−1). However, as pointed out in Ref. [4: ISO 80000-3], the designations “revolutions per second” (r/s) and “revolutions per minute” (r/min) are widely used as units for rotational frequency in specifications on rotating machinery."[2]
- ↑ "The SI unit of frequency is hertz, the SI unit of angular velocity and angular frequency is radian per second, and the SI unit of activity is becquerel, implying counts per second. Although it is formally correct to write all three of these units as the reciprocal second, the use of the different names emphasizes the different nature of the quantities concerned. It is especially important to carefully distinguish frequencies from angular frequencies, because by definition their numerical values differ by a factor [see ISO 80000-3 for details] of 2π. Ignoring this fact may cause an error of 2π. Note that in some countries, frequency values are conventionally expressed using “cycle/s” or “cps” instead of the SI unit Hz, although “cycle” and “cps” are not units in the SI. Note also that it is common, although not recommended, to use the term frequency for quantities expressed in rad/s. Because of this, it is recommended that quantities called “frequency”, “angular frequency”, and “angular velocity” always be given explicit units of Hz or rad/s and not s−1."[3]
References
- ↑ Atkins, Tony; Escudier, Marcel (2013). A Dictionary of Mechanical Engineering. Oxford University Press. ISBN 9780199587438. http://www.oxfordreference.com/view/10.1093/acref/9780199587438.001.0001/acref-9780199587438-e-5953?rskey=EBYJmx&result=1.
- ↑ "The NIST Guide for the Use of the International System of Units, Special Publication 811". National Institute of Standards and Technology. 2020-03-04. https://www.nist.gov/pml/special-publication-811. [1]
- ↑ International Bureau of Weights and Measures (2019-05-20), SI Brochure: The International System of Units (SI) (9th ed.), ISBN 978-92-822-2272-0, https://www.bipm.org/utils/common/pdf/si-brochure/SI-Brochure-9.pdf
- ↑ "ISO 80000-3:2019 Quantities and units — Part 3: Space and time". International Organization for Standardization. 2019. https://www.iso.org/standard/64974.html. [2] (11 pages)
- ↑ "Rotational Quantities". http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html.
